Geometry, Surfaces, Curves, Polyhedra
The following is a random collection of various topics in geometry the author has explored or
simply documented over the years. Many of the topics include source code illustrating how to solve
various geometric problems, or to assist others recreating the geometric forms presented.
Notes on polygons and meshes
Includes Surface (polygon) simplification,
Clipping a polygonal facet with an arbitrary plane,
Surface Relaxation and Smoothing of polygonal data,
Mesh crumpling, splitting polygons, two sided facets, polygon types,
tests for clockwise and concavity, clipping line to polygons, area of a 3D polygon,
area of general polygons, determining inside/outside test, intersection of a line
and a facet, Eulers numbers.
Notes on points, lines and planes
Includes calculations for the distance between points, lines and planes.
The intersection between 2 lines in 2D and 3D, the intersection of a line with a plane.
The intersection of two and three planes.
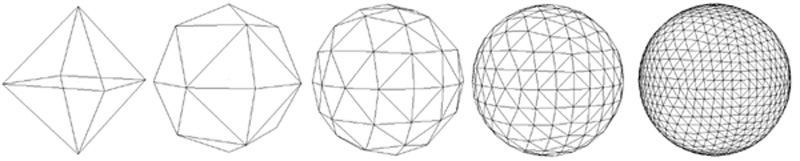
Notes on circles, cylinders and spheres
Includes equations and terminology.
Equation of the circle through 3 points and sphere thought 4 points.
The intersection of a line and a sphere (or a circle).
Intersection of two circles on a plane and two spheres in 3D.
Distributing Points on a Sphere.
The area of multiple intersecting circles.
Creating a plane/disk perpendicular to a line segment.
Modelling with spheres and cylinders,
including facet approximation to a sphere and cylinder, rounded boxes, pipes, and modelling with spheres.
The most important thing in the programming language is the name. A
language will not succeed without a good name. I have recently
invented a very good name and now I am looking for a suitable language.
D. E. Knuth, 1967
Transformations and projections
Methods for mapping points on a spherical surface onto a plane,
stereographic and cylindrical (including Mercator) projections.
Includes Aitoff map projection: Conversion to/from longitude/latitude (spherical map).
Transformations on the plane.
Cartesian, Cylindrical, and Spherical coordinate systems.
Euler angles and coordinate transformations.
Converting between left and right coordinate systems.
Classification of projections from 3D to 2D and specific examples of oblique projections.
Planar (stretching) distortion in the plane.
Anamorphic projections and Mappings in the Complex Plane (Otherwise known as Conformal maps).
3D projection: Transforming 3D world coordinates into 2D screen coordinates.
Convert spherical projection into a cylindrical projection.
Uniform vector on sphere given rotation angles
Tiling textures
An introduction to texture tiling using characteristics of the texture itself.
A general method is presented that converts any texture into one that tiles without seams.
Illustrates the most common texture mapping methods in use by rendering applications. The
mathematics of how to map a rectangular texture onto a sphere, creating a textured mesh in
OpenGL and how to correct for polar distortion of texture maps on spheres.
Texture library
Tiling on the plane and more recently
Tiling tricurves
Includes Truchet tiling in 2D and 3D, Regular pentagonal tiles,
block tessellation, weaving, and more.
Non periodic (aperiodic) tiling of the plane:
Methods of tiling that are never periodic, for example,
Penrose tiles, Danzer tiles, Chair tiles, Trilobite tiles, Pinwheel tiles.
Decagon tiles and truncated decagons.
Most of the tiles are presented accurately and large enough to be printed and cut out.
Hexagonal tiling and SHM Calculator
Including MacOS-X and Linux software for experimenting with transformation in the Spiral Harmonic Mosaic.
Relationship between base 7 and base 10:
Exploration by Paolo Di Pasquale © 1988-2012
Philosophy is written in this grand book - I mean universe - which
stands continuously open to our gaze, but which cannot be understood
unless one first learns to comprehend the language in which it is
written. It is written in the language of mathematics, and its
characters are triangles, circles and other geometric figures, without
which it is humanly impossible to understand a single word of it;
without these, one is wandering about in a dark labyrinth.
Galileo (1623)
Contouring Algorithm
Description of an efficient contouring algorithm
as it appeared in Byte magazine. (Byte Magazine, 1987) and a more
general approach for arbitrary contour planes and polygonal meshes.
Polygonising a scalar field
Otherwise known as marching cubes and marching tetrahedrons.
HyperSpace
Notes on 4 dimensional geometry, including an old
Macintosh 4 dimensional geometry viewer and manual.
List of 4D platonic solids and the coordinates for 4D polyhedra.
There are holes in the sky. Where the rain gets in.
But they're ever so small. That's why the rain is thin.
Spike Milligan
Of cube nature
SGI logo, Wiffle cube, Rounded cube, Tooth surface, Horned cube,
Tangle surface
Of spherical and elliptical nature
Models of sports balls, Prolate spheroid, Cymbelloid, Superellipse, Superellipsoid,
Capsules, Eggs, Melons, Peanuts, Cassini Oval, Ellipse, Apple, Baseball curve,
Cassinoid, Cassinian Ellipse.
Circumference of an ellipse and arc approximation
The circumference of an ellipse,
one might think this was a "solved" problem, nothing could be further from the truth.
Of toroidal nature
Torus, Supertorus, Klein bottle, Möbius strip,
Elliptic Torus, Limpet Torus, Gumdrop torus, Figure 8 Torus,
2-Torus, Saddle torus, Kinky Torus, Bow tie, Triaxial Tritorus,
Triaxial Hexatorus, Twisted pipe, Double torus, Bow curve,
Bretzel, Pretzel, Pisot triaxial
Of spiral nature
Horn, Cresent, Sea shells, Springs, Dini surface, Equiangular spiral, Parabolic spiral,
Hyperbolic spiral, Fermats spiral, Lituus Spiral, Archimedes spiral, Sinusoidal spiral,
Square Archimedes spiral, Cornu spiral, Tanh spiral, Coth spiral, Helix,
Clothoid, Eulers Spiral
You may say I'm a hacker, But I'm not the only one.
I hope someday you'll join us, And the world will code as one.
Waterman Polyhedra
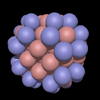
|
Cylinder intersections

|
Plexagons
|
Platonic solids

|
Verrill

|
Time Star

|
Polar + Star sphere

|
Parallelohedron
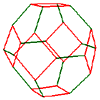
|
SuperShape

|
80 Polyhedra
|
Tetrakaidecahedron
|
Pyritohedron
|
Islamic Art
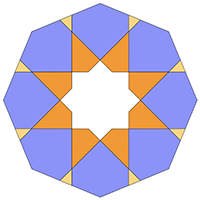
|
Trisagita tiles
|
Hyperboloid
|
To see a World in a Grain of Sand, And Heaven in a Wild Flower.
Hold Infinity in the palm of your hand, And Eternity in an hour. William Blake
|
Photos by Gayla Chandler

|
Meta logo

|
Build your own
|
Kuen's

|
Implicit Surfaces
|
Polyhedra data files

|
Spherical Harmonics

|
Inverse Truchet

|
Pseudosphere

|
Harmonograph
|
Experience hath shown, that even under the best forms of government those
entrusted with power have, in time, and by slow operations, perverted it into tyranny.
Thomas Jefferson
|
Borg

|
Bifolia

|
Twisted plane

|
Twisted Fano

|
Cross Hole

|
Chair

|
Fano planes

|
Tranguloid Trefoil

|
Chladni plates

|
Nose

|
Aesthetic delight lies somewhere between boredom and confusion. E. H. Gombrick
|
Witch hat

|
Slipper
|
Decocube

|
Strophoid

|
3D shape filling

|
2D Bow curve
|
Cross Cap
|
Steiner
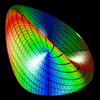
|
Hunt
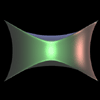
|
Stiletto
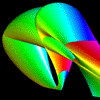
|
A straight line may be the shortest distance between two points,
but it is by no means the most interesting.
|
Barth Decic

|
Twisted Triaxial
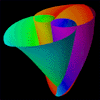
|
Mitre

|
Nodal cubic

|
Boy

|
Klein Cycloid

|
Jet

|
Heart surfaces

|
Pilz

|
Tear drop

|
"I know what you're thinking about," said Tweedledum; "but it isn't so, nohow."
"Contrariwise," continued Tweedledee, "if it was so, it might be,
and if it were so, it would be, but as it isn't, it ain't That's logic"
Lewis Carroll
|
Tubey
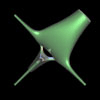
|
Maeder's Owl
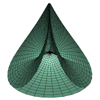
|
Spline curve/surface

|
Triaxial teardrop

|
Whitney umbrella
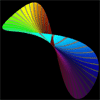
|
Lemniscape
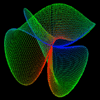
|
Tractrix

|
Pseudocatenoid

|
Twisted heart

|
Piva surface
|
Going to war over religion is basically killing each other to see who's got the
better imaginary friend. Richard Jeni
|
Calabi-Yau

|
Hexagonal Drum

|
OrthoCircle

|
Barth sextic

|
Folium

|
Devil
|
Swallow
|
P1 atomic orbital

|
Ghost Plane
|
Bent Horns

|
The only thing that saves us from the bureaucracy is its inefficiency.
|
Catenoid minimal
|
Helicoid minimal

|
Bour minimal
|
Ennepers minimal
|
Richmond minimal

|
Handkerchief
|
Scherk minimal
|
Kidney

|
Monkey saddle
|
Pillow shape
|
I don't do drugs. If I want a rush then I get out of the chair when I'm not expecting it.
Dylan Moran
|
Cushion
|
Double Cone
|
Catalan minimal

|
Fish

|
Cayley
|
2D tiles from 3D

|
Chainmail
|
dForm
|
Mecon tiles
|
Durehedron

|
There is a remote tribe that worships the number zero. Is nothing sacred?
Les Dawson
|
Snail
|
The Blob

|
Kusner Schmitt
|
McMullen K3 model
|
Tri-Trumpet

|
Weird

|
Gerhard Miehlich
|
Kampyle of Eudoxus

|
Tetra Ellipse

|
Sextics

|
I believe the geometric proportion served the creator as an idea
when He introduced the continuous generation of similar
objects from similar objects. Johannes Kepler
|
Spherical tiles

|
Small Rhombicuboctahedron
|
Rhombic triacontahedron
|
Animated Tiles

|
Kolam and Rangoli

|
Borromean rings

|
Mesh weave
|
Knots

|
Chrysanthemum

|
Love Heart
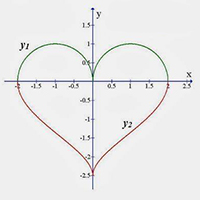
|
Bezier curves/surfaces
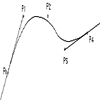
|
Henneburg minimal

|
Gerono lemniscate

|
Cycloid
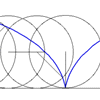
|
Conic sections
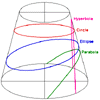
|
If triangles had a God, He'd have three sides. Old Yiddish proverb
|
Butterfly curve

|
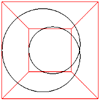
Viviani curve
|
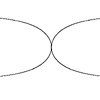
Kappa curve
|
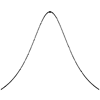
Agnesi curve
|
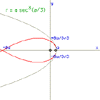
Cayleys sextic
|
Hypocycloid
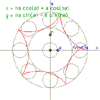
|
Freeths Nephroid
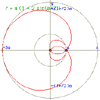
|
Tractrix

|
Spherical Nephroid
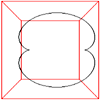
|
Epicycloid
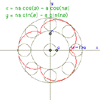
|
We should make things as simple as possible, but not simpler. Albert Einstein
|
Conchoid of Nicomedes
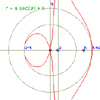
|
Cissoid of Diocles
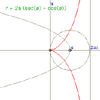
|
Deltoid
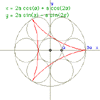
|
Strophoid
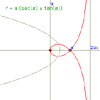
|
Lemniscate Bernoulli
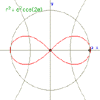
|
Astroid
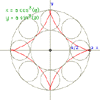
|
Nephroid
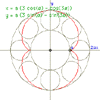
|
Spherical Cardioid
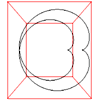
|
Cardioid
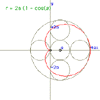
|
Parabola
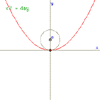
|
No amount of genius can overcome a preoccupation with detail. Law 8, Marion Levy Jr.
|
Hyperbola
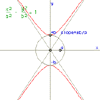
|
Diamond curve
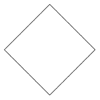
|
Folium curve

|
Limacon
|
Trisectrix of Maclaurin
|
Reuleaux Triangle
|
Network

|
Blobbie

|
Bicorn curve
|
Glissette
|
I was walking down the street when I saw a dead baby ghost on the road.
On reflection it might have been a handkerchief.
Milton Jones

Mt Woodroffe, South Australia
Other ...
POV-Ray: A Tool for Creating Engaging Visualisation of Geometry
Solid angle of a pixel
Reflection of a ray
Direction Cosines
Rotation of a point about an arbitrary axis
Quadric equations in x and y of degree 2
Fowler angles: Comparing angles without trigonometry
Why do kamikaze pilots wear helmets? Smacks of indecision to me.
Sean Mea
|
Contents:
Papers, Presentations, Workshops −
Geometry, Surfaces, Curves, Polyhedra −
Fractals, Chaos, Self similarity −
Domes, Planetariums, Fisheye, Spherical Mirror −
Stereoscopy, 3D Projection −
Panorama, 360 Video −
Photographic Reconstruction −
Miscellaneous: Projection, Modelling, Rendering −
Data Formats: 3D, Audio, Image −
Texture Library −
Fun, Puzzles, Travel
(All pages in one place)
Recent:
Preparing video from the Canon RF 5.2mm f/2.8L Dual Fisheye lenses for screen display −
Cortical Development in the Structural Model and Free Energy Minimization −
Digitising the Murten Panorama. The story behind the highest resolution
scan of an artwork −
Vertical Panoramas −
Symmetry in Chaos −
Tools for Spherical Mirror Projection
Copyright:
The contents of this web site are © Copyright Paul Bourke or
a third party contributor where indicated.
You may print or save an electronic copy of parts of this web site for personal use,
permission must be sought for any other use.
|
|