Rotate a point
about an arbitrary axis
(3 dimensions)
Written by Paul Bourke
December 1992, Updated August 2002
Illustrative C code that implements the following algorithm is
given here.
A closed solution attributed to Ronald Goldman is presented as this
C function.
A contribution by Bruce Vaughan in the form of a Python script
for the SDS/2 design software: PointRotate.py.
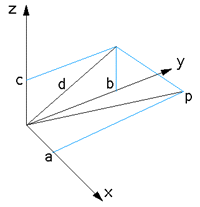
Rotation of a point in 3 dimensional space by theta
about an arbitrary axes defined by a line between
two points P1 =
(x1,y1,z1) and P2 =
(x2,y2,z2) can be achieved by
the following steps
(1) translate space so that the rotation axis passes through the
origin
(2) rotate space about the x axis so that the rotation axis lies in the
xz plane
(3) rotate space about the y axis so that the rotation axis lies along
the z axis
(4) perform the desired rotation by theta about the z axis
(5) apply the inverse of step (3)
(6) apply the inverse of step (2)
(7) apply the inverse of step (1)
Note:
If the rotation axis is already aligned with the z axis then
steps 2, 3, 5, and 6 need not be performed.
In all that follows
a right hand coordinate system is assumed and rotations are positive
when looking down the rotation axis towards the origin.
Symbols representing matrices will be shown in bold text.
The inverse of the rotation matrices below are particularly
straightforward since the determinant is unity in each case.
All rotation angles are considered positive if anticlockwise looking
down the rotation axis towards the origin.
Step 1
Translate space so that the rotation axis passes through the origin.
This is accomplished by translating space by
-P1 (-x1,-y1,-z1).
The translation matrix T and the inverse T-1
(required for step 7) are given below
| T = |
 |
| 1 | 0 | 0 | -x1 |
| 0 | 1 | 0 | -y1 |
| 0 | 0 | 1 | -z1 |
| 0 | 0 | 0 | 1 |
|
 |
|
|
| T-1 = |
 |
| 1 | 0 | 0 | x1 |
| 0 | 1 | 0 | y1 |
| 0 | 0 | 1 | z1 |
| 0 | 0 | 0 | 1 |
|
 |
|
Step 2
Rotate space about the x axis so that the rotation axis lies in the xz plane.
Let U = (a,b,c) be the unit vector along the rotation axis.
and define d = sqrt(b2 + c2)
as the length of the projection onto the yz plane.
If d = 0 then the rotation axis is along the x axis and no
additional rotation is necessary.
Otherwise rotate the rotation axis so that is lies in the xz plane.
The rotation angle to achieve this
is the angle between the projection of rotation axis in
the yz plane and the z axis. This can be calculated from the dot product of the
z component of the unit vector U and its yz projection.
The sine of the angle is determine by considering the cross product.
| |
(0,0,c) dot (0,b,c) |
|
| cos(t) = |
|
= c/d |
| |
c d |
|
|
|
| |
|| (0,0,c) cross (0,b,c) || |
|
| sin(t) = |
|
= b/d |
| |
c d |
|
|
The rotation matrix Rx and the inverse
Rx-1 (required for step 6) are given below
| Rx = |
 |
| 1 | 0 | 0 | 0 |
| 0 | c/d | -b/d | 0 |
| 0 | b/d | c/d | 0 |
| 0 | 0 | 0 | 1 |
|
 |
|
|
| Rx-1 = |
 |
| 1 | 0 | 0 | 0 |
| 0 | c/d | b/d | 0 |
| 0 | -b/d | c/d | 0 |
| 0 | 0 | 0 | 1 |
|
 |
|
Step 3
Rotate space about the y axis so that the rotation axis lies along the
positive z axis.
Using the appropriate dot and cross product relationships as before the cosine
of the angle is d, the sine of the angle is a.
The rotation matrix about the y axis Ry
and the inverse Ry-1
(required for step 5) are given below.
| Ry = |
 |
| d | 0 | -a | 0 |
| 0 | 1 | 0 | 0 |
| a | 0 | d | 0 |
| 0 | 0 | 0 | 1 |
|
 |
|
|
| Ry-1 = |
 |
| d | 0 | a | 0 |
| 0 | 1 | 0 | 0 |
| -a | 0 | d | 0 |
| 0 | 0 | 0 | 1 |
|
 |
|
Step 4
Rotation about the z axis by t (theta) is Rz and is
simply
| Rz = |
 |
| cos(t) | -sin(t) | 0 | 0 |
| sin(t) | cos(t) | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
|
 |
The complete transformation to rotate a point (x,y,z) about the rotation
axis to a new point (x`,y`,z`) is as follows, the forward transforms
followed by the reverse transforms.
 |
|
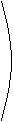 |
= |
T-1
Rx-1
Ry-1
Rz
Ry
Rx
T
|
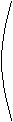 |
|
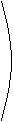 |
Using quaternions
To rotate a 3D vector "p" by angle theta about a (unit) axis "r" one forms the
quaternion
Q1 = (0,px,py,pz)
and the rotation quaternion
Q2 = (cos(theta/2), rx sin(theta/2),
ry sin(theta/2), rz sin(theta/2)).
The rotated vector is the last three components of the quaternion
Q3 = Q2 Q1 Q2*
It is easy to see that rotation in the opposite direction (-theta) can be
achieved by reversing the order of the multiplication.
Q3 = Q2* Q1 Q2
Note also that the quaternion Q2 is of unit magnitude.
| 