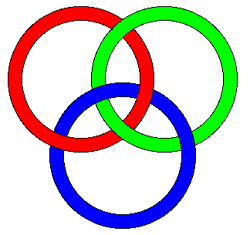
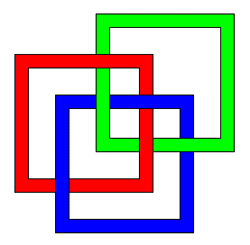
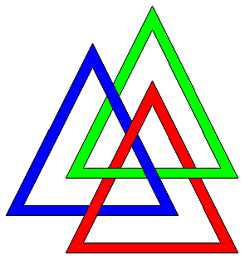
Borromean Rings Written by Paul Bourke October 1997 Borromean rings are three interlinked rings such that no two rings are linked. In other words, the three rings cannot be separated and yet no two of them are linked. It can be shown that there is no solution for flat rings, it can only be constructed by perturbing the rings in a third dimension. The rings can be formed with various base geometries including rectangles and triangles as shown below.

One way (as shown below) to create the rings mathematically is with the following three parametric equations, one for each ring.

           (cos(u)       , sin(u) + r   , cos(3u) / 3)
           (cos(u) + 0.5 , sin(u) - r/2 , cos(3u) / 3)
           (cos(u) - 0.5 , sin(u) - r/2 , cos(3u) / 3)

This is illustrated below for r = sqrt(3)/3, the radius of the spheres placed along the path is 0.2

It is possible to make the rings out of elliptical rings, it does require 3 dimensions. The parametric equations for the three "rings" are

           (     0     , r1 cos(u) , r2 sin(u) )
           ( r2 cos(u) ,     0     , r1 sin(u) )
           ( r1 cos(u) , r2 sin(u) ,     0     )

This is illustrated below for r1 = 2, r2 = 1, and the radius of the tubes = 0.2

Featured on the cover of the HPC (High Performance Computing) magazine, 20 July 2001.

And finally, using box geometry...

Contribution by Robert McGrego

Contribution by Lindsay Taylor. "Each of the 3 links was created using a mesh supertoroid script and is an interlocked pair of (4, 3) torus knots."