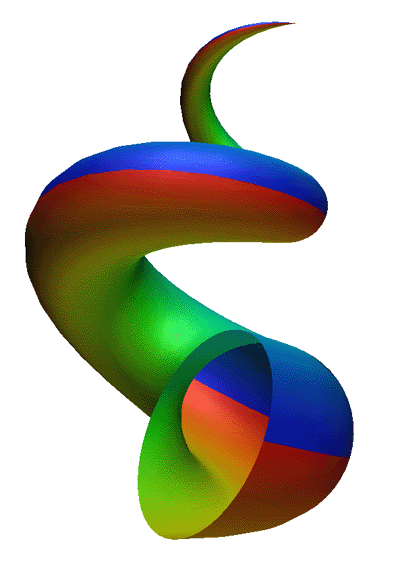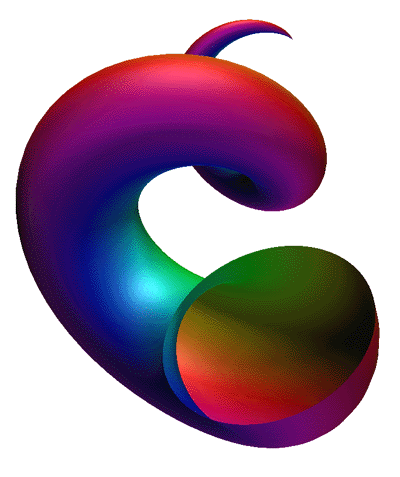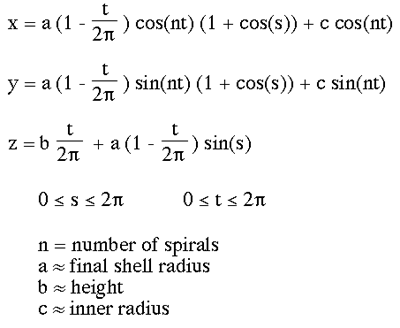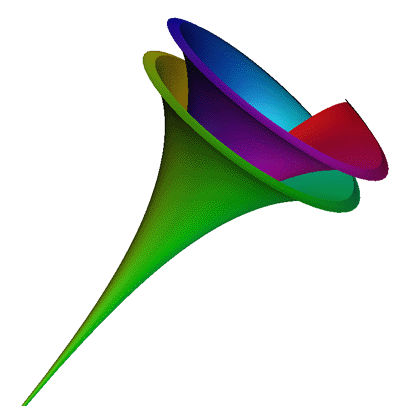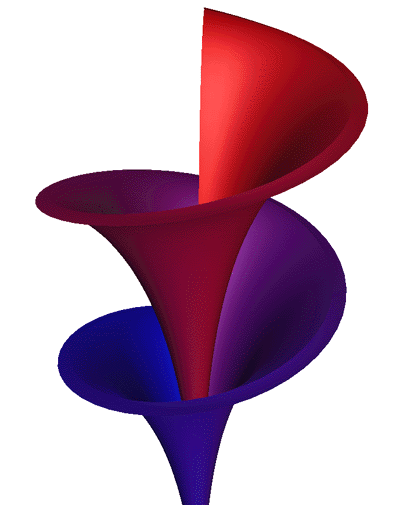HornGraphics by Paul BourneMarch 2002
y = (2 + u cos(v)) cos(2 pi u) + 2 u z = u sin(v) 0 <= u <= 1, 0 <= v <= 2π

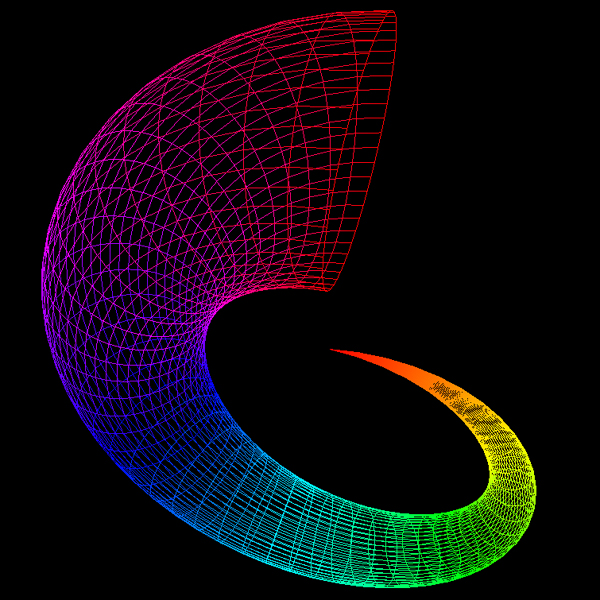
CrescentBy Paul BurkeAugust 2002
y = (2 + sin(2 π u) sin(2 π v)) cos(3 π v) z = cos(2 π u) sin(2 π v) + 4 v - 2 0 <= u <= 1, 0 <= v <= 1




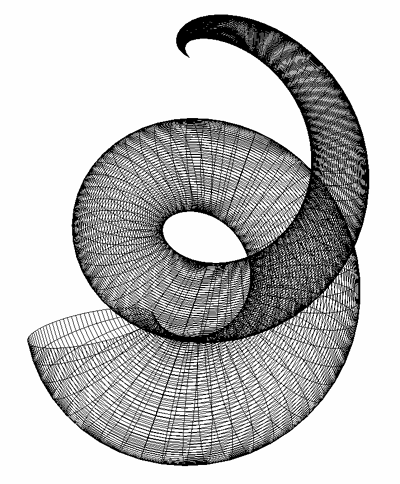
Mathematical Sea ShellCreated by Paul BourkeMay 1989
Modelling SpringsWritten by Paul BourkeNovember 2000 r1 = 0.25, r2 = 0.25, periodlength=3.0, cycles = 4 Introduction This note describes one of many ways to describe a spring. The method used here is chosen because of the ease in which it can be used to describe a spring in a format suitable for computer modelling and rendering packages. 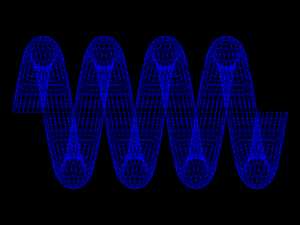
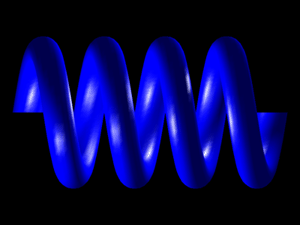
r1 = 0.5, r2 = 0.5, periodlength=1.5, cycles = 3 Formula The formula below gives a point on the surface of a spring in Cartesian coordinates. It is a parametric equation in terms of parameters u and v. Both range from 0 to 2 pi, increasing u will give multiple windings. y = [1 - r1 * cos(v)] * sin(u) z = r2 * [sin(v) + periodlength * u / pi] Using these formula to create the 4 vertices of facets is fairly straightforward, see the C source code given below. Basically one evaluates the function for the parameters (u,v), (u+du,v), (u+du,v+dv), (u,v+dv) where du and dv are small increments, the exact amount depends on how smoothly one wants the surface to be represented. 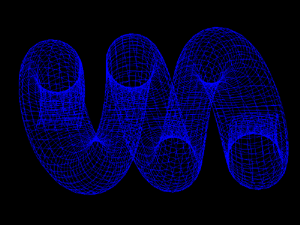
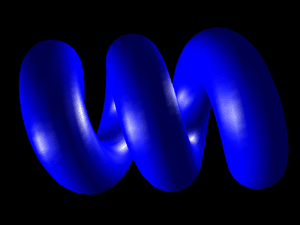
r1 = 0.2, r2 = 0.2, periodlength=1.0, cycles = 3 Examples The examples below illustrate a small subset of the springs that can be created using the above formula. The parameters shown in red beside each example should make sense. For example, the number of cycles can be counted on the springs. The length of one winding is called the periodlength. The two radii determine the cross-section of the spring, circles for when r1 = r2 and squashed rings when r1 != r2. 

r1 = 0.2, r2 = 0.5, periodlength=1.5, cycles = 3 Extensions Some exercises for the reader.....(1) this can easily be turned into a spring spiral by scaling the x and y values by some function of u. (2) Many rendering programs might insist on descriptions of solid objects in which case a cap will be needed on the ends of the spring. (3) The resolution of the facet approximation could be automatically determined by the number of cycles. 

r1 = 0.5, r2 = 0.2, periodlength=1.5, cycles = 5
Source code A simple piece of C code is given here: spring.c. It creates a faceted approximation to a spring including the calculation of unit normals for smooth shading. In this example the facets are written in geom format, it should be easy to modify the code to export in a format suited to your application. The images given here were rendered using OpenGL. 

It is pointed out that a distortion occurs for large values of periodlength. The proposed correction for the value of z is as follows: z = r2 * sin(v) * sqr(1+(periodlength / pi)*(periodlength / pi)) + periodlength * u / piAlternatively reformulated as follows
x = [R - r * cos(v)] * cos(u) where h = periodlength / pi Or alternatively
x = [R + r * cos(v)] * cos(u) + h * r * sin(v) * sin(u) / w Dini's Surface or Twisted Pseudo-sphereWritten by Paul BourkeOctober 1995
Surface of constant curvature (negative).
Equiangular spiralAlso known as the logarithmic spiral

Fermat's spiral
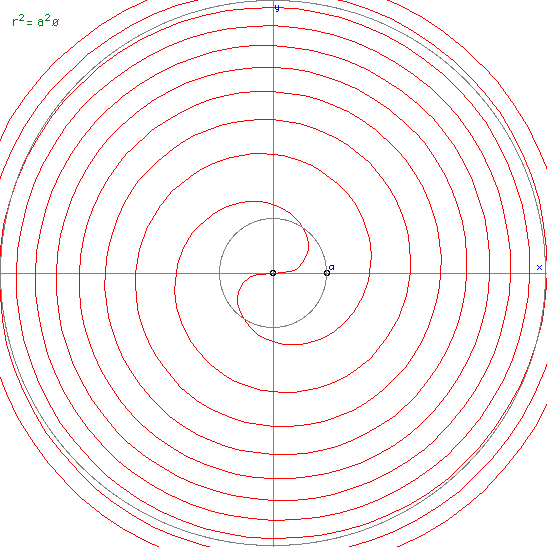
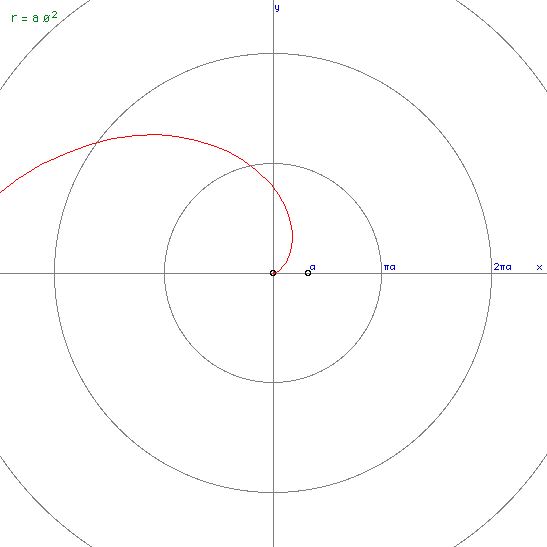
Parabolic spiral

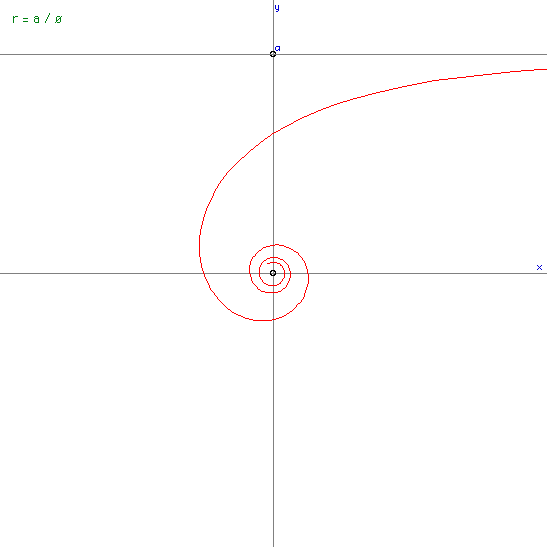
Hyperbolic spiralAlso known as the reciprocal spiral
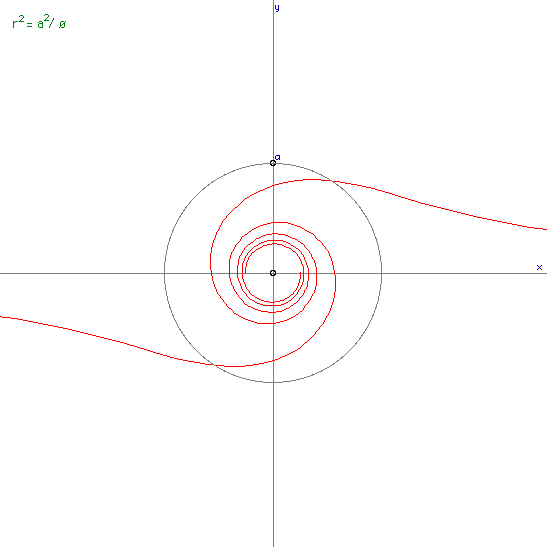
Lituus spiral
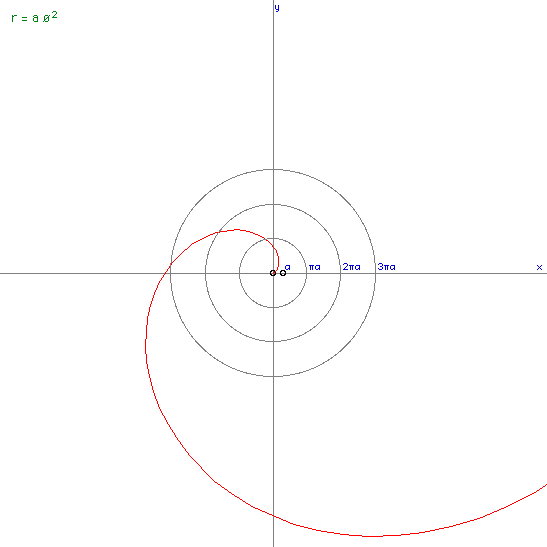
Sinusoidal spiral

Square Archimedes spiral
Cornu SpiralAlso known as Clothoid and Eulers Spiral
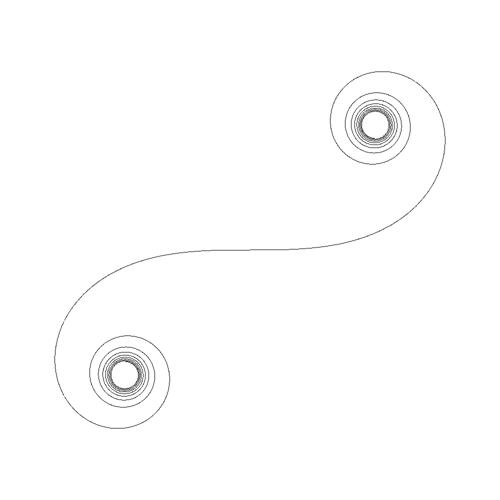
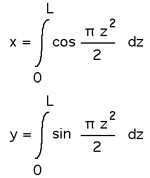
These curves were most likely first studied Johann Bernoulli in the 1690's.
Tanh SpiralBy Paul BourkeJanuary 2001
y = sin(2 a t) / (cos(2 a t) + cosh(2 t)) -π/2 <= t <= π/2, a > 0 (eg: 2)

Coth SpiralBy Paul BourkeJanuary 2001
y = sin(2 a t) / (cos(2 a t) - cosh(2 t)) -π/2 <= t <= π/2, a > 0 (eg: 4)

HelixBy Paul BourkeJanuary 2001
y = sin(t) z = a t 0 < t < 4 π, a = 0.2 (for example)
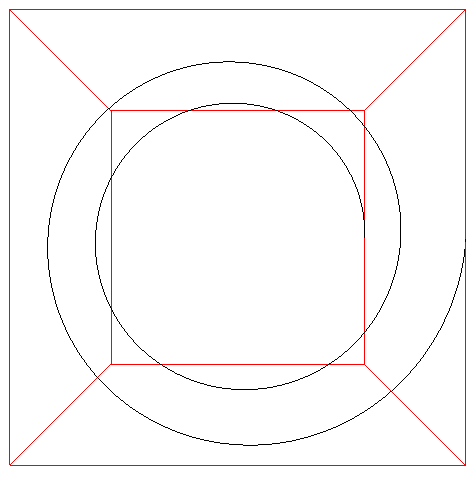
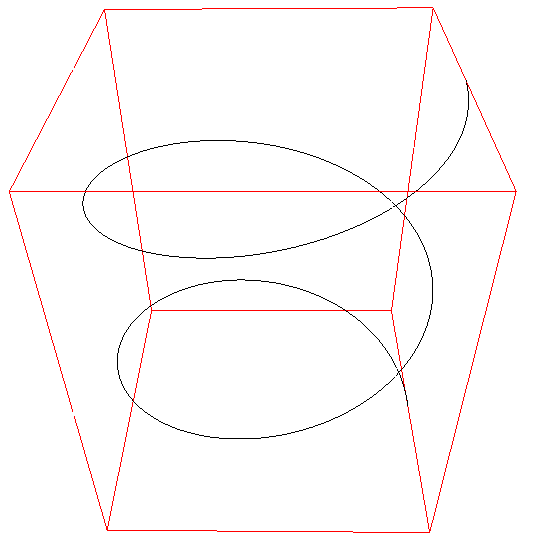
|