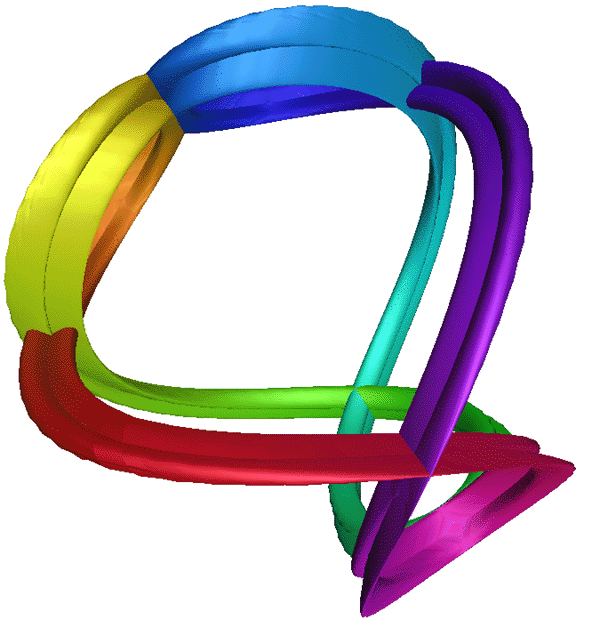Klein Cycloid

Banchoff's Kleinbottle
Reference: C. Pickover's "Mazes for the Mind" Page 100
Converted into a cycloid by Roger Bagula © (July 1997)

Graphics by Paul Bourke
September 1998

Parametric definition

x = cos(u/c) * cos(u/b) * (a + cos(v)) + sin(u/b) * sin(v) * cos(v)
y = sin(u/c) * cos(u/b) * (a + cos(v)) + sin(u/b) * sin(v) * cos(v)
z = -sin(u/b) * (a + cos(v)) + cos(u/b) * sin(v) * cos(v)
Where
0 <= u <= 2 b c π and 0 <= v <= 4 π

Appeared on the October 5, 2001 (Vol 10 No 40) issue of HPC magazine.

C source, generating an OOGL file

#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "paulslib.h"

int main(int argc,char **argv)
{
   int i,j,nu=200,nv=50;
   double u,v;
   double a=10.0,b=3,c=2;
   XYZ p;
   COLOUR colour;
   COLOUR black = {0.0,0.0,0.0};

   if (argc < 4) {
      fprintf(stderr,"Usage: %s a b c\n",argv[0]);
      exit(0);
   }
   a = atof(argv[1]);
   b = atof(argv[2]);
   c = atof(argv[3]);

   printf("CMESH\n%d %d\n",nv+1,nu+1);
   for (i=0;i<=nu;i++) {
      for (j=0;j<=nv;j++) {

         u = i * 2 * b * c * PI / nu;
         v = j * 4 * PI / nv;

         p.x = cos(u/c) * cos(u/b) * (a + cos(v)) + sin(u/b) * sin(v) * cos(v);
         p.y = sin(u/c) * cos(u/b) * (a + cos(v)) + sin(u/b) * sin(v) * cos(v);
         p.z = -sin(u/b) * (a + cos(v))           + cos(u/b) * sin(v) * cos(v);

         colour = GetColour(u,0.0,2*b*c*PI,4);
         printf("%g %g %g %g %g %g 0.5\n",p.x,p.y,p.z,
            colour.r,colour.g,colour.b);
      }
   }
}

Mathematica code

(by R. L. Bagula, 2 July 1997)

a=10;
b=3;
c=2;
X=Cos[u/c]*Cos[u/b]*(a+Cos[v])+Sin[u/b]*Sin[v]*Cos[v];
Y=Sin[u/c]*Cos[u/b]*(a+Cos[v])+Sin[u/b]*Sin[v]*Cos[v];
Z=-Sin[u/b]*(a+Cos[v])+Cos[u/b]*Sin[v]*Cos[v];

ParametricPlot3D[{X, Y, Z}, {u, 0, 2*b*c*Pi}, {v, 0, 4 Pi},
        PlotPoints -> {120,10}, Axes -> False, Boxed -> False,
                 ViewPoint->{5.265, -6.828, 2.580}];