Tetrakaidecahedron and Pyritohedron

Introduction

The following presents some results around experiments with the Tetrakaidecahedron and Pyritohedron solids. These solids arise from finding a packing for soap bubbles that have minimal shared surface area (minimum energy), these are known as Wearie-Phelan bubbles.

A minimal packing involving a single shape is a truncated octahedron shown below. Such a minimal surface energy requires 3 bubbles to meet at every edge and 4 to meet at every vertex. It is also required that the tetrahedral angle is the same which turns out to be impossible for polyhedra. So in the minimal energy state the edges are not straight nor the faces flat, both curve slightly.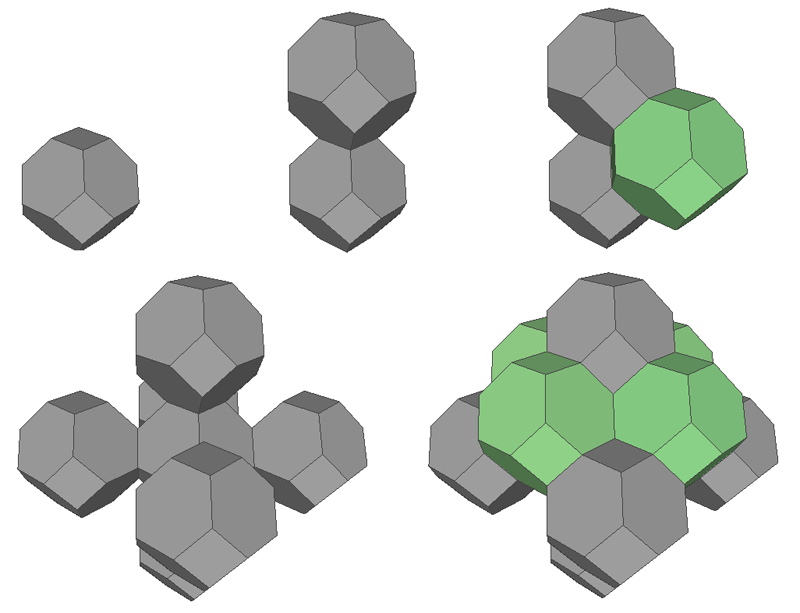

A lower energy solution requires two differently shaped, but equal size, bubbles. These are the tetrakaidecahedron (top) and pyritohedron (bottom) solids illustrated below. Unlike the truncated octahedron the faces are not necessarily regular. The is often also called a tetradecahedron but that generally refers to a whole family of solids, some of which are regular.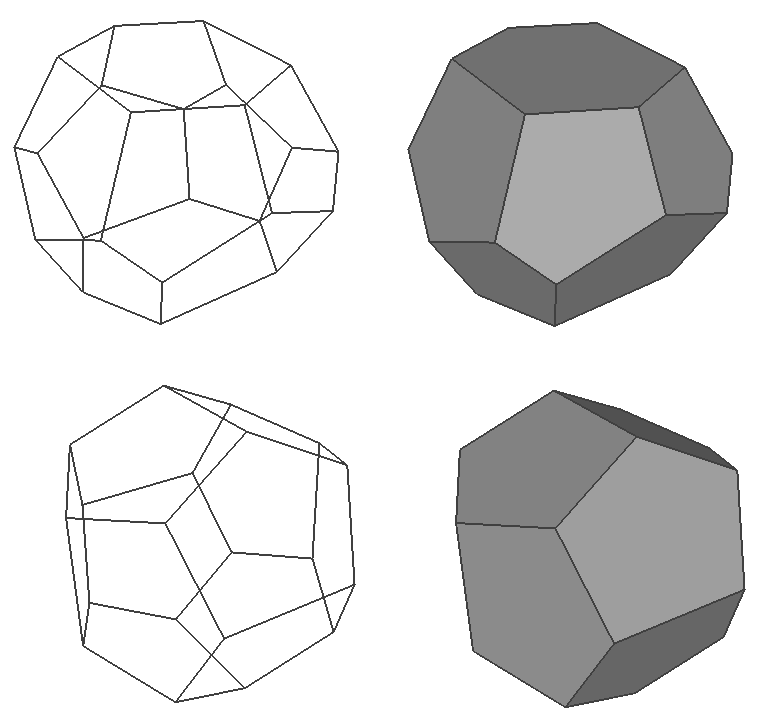

Examples of the tiling is shown below.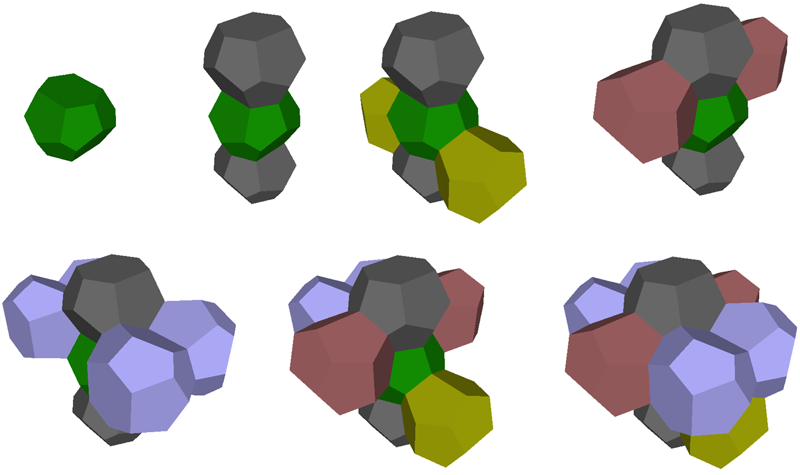

The tetrakaidecahedras form straight line chains along three axes.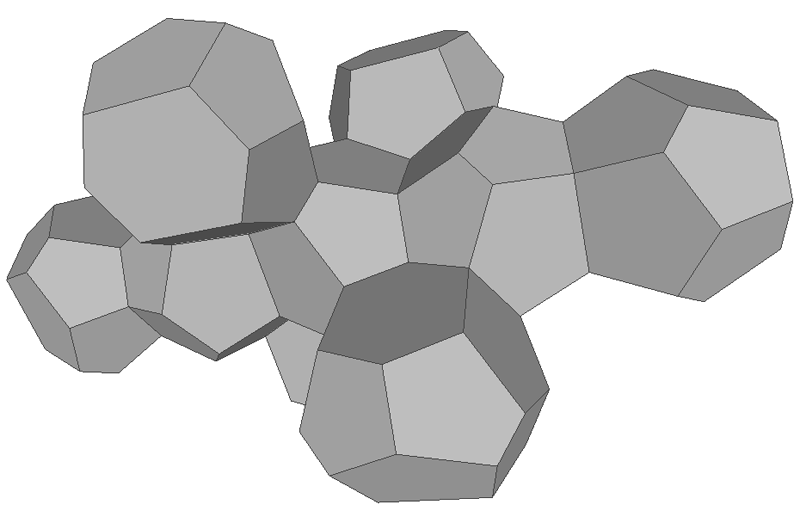

Models

OBJ files for each solid are provided so the reader can play along at home. These include the vertices, faces (decomposed into triangles) and all faces have a consistent normal orientations. The vertices have been scaled such that tiling occurs using translations that are integer multiples of 5 (or 10).

• Tetrakaidecahedron
  
• Pyritohedron
  
• TruncatedOctahedron
  
• Single 5 or 6 vertex polygons (for software that is OK with that): Tetrakaidecahedron.
  
• Single 5 or 6 vertex polygons: Pyritohedron.
  

Notes

• The pyritohedron has 12 mirror symmetric irregular pentagons, 30 edges and 20 vertices.
  The tetrakaidecahedron has 14 faces, two are hexagonal and the remainder pentagonal. It has 24 vertices and 36 edges.

• The pyritohedron is similar to the dodecahedron in that it consists of entirely pentagonal faces, but differs in that the edge lengths are not all the same. The name is derived from the pyrite crystal which has the same shape.

• It turns out that in the tiling the pyritohedra do not touch each other but are rather totally surrounded by the tetrakaidecahedra.