Many projection environments require images that are not simple perspective projections that are the norm for flat screen displays. Examples include geometry correction for cylindrical displays and some new methods of projecting into planetarium domes or upright domes intended for VR. The standard approach is to create the image in a format that contains all the required visual information and distort it (from now on referred to as "warping") to compensate for the non planar nature of the projection device or surface. For both realtime and offline warping the concept of a OpenGL texture is used, that is, the original image is considered to be a texture that is applied to a mesh defined by node positions and corresponding texture coordinates, see figure 1. The following describes a file format for storing such warping meshes, it consists of both an ascii/human readable format and a binary format.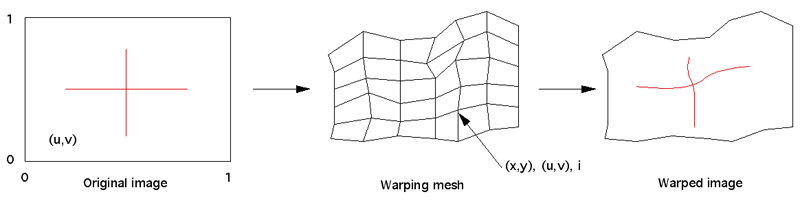

Figure 1. Image applied as a texture to a mesh, each node is defined by a position (x,y) and texture coordinate (u,v).

The warping can be performed in either the x,y coordinates (Figure 2) or in the u,v coordinates (Figure 4) or in both. This flexibility allows the method used to be chosen that best matches the way the mesh is derived, sometimes it is easier to derive the u,v coordinates given the x,y coordinates, other times the reverse is so.

Full panoramic image.

Warping mesh.

Resulting warped image.

Figure 2. Example warping a panoramic image for a cylindrical display.
The warping is encoded in the x,y node positions, the u,v coordinates are a regular grid.

File format

• First line contains the mesh type, currently rectangular (2) and polar (1) are supported, see figure 3. The only significant difference between these two is the mesh continuity that occurs for the polar mesh across the 0 and 360 degree boundary.

• Second line contains two integers indicating the mesh dimensions, nx and ny.

• The subsequent lines define the nodes, there should be nx times ny lines. These lines contain 5 values defined as follows.

  • Position x and y of the node in normalised coordinates. The mesh need not exactly match the projected image, in figure 2 it actually extends off the projected region while in figure 4 it matches the 4:3 aspect exactly. In the later case the horizontal range (x) will be +- the aspect ratio and the vertical range (y) will be +- 1 (ie: OpenGL style normalised coordinates).

  • Texture coordinate u and v, these should each range from 0 to 1, they refer to the original input image. Values outside the 0 to 1 range indicate that the node is not to be used, this usually means the mesh cells sharing that node are not used but sometimes it is appropriate to triangulate the mesh for such cells.

  • A multiplicative intensity value applied to each r,g,b colour value. The can be used for simple edge blending and to compensate for brightness variation due to different light path lengths from projector to projection surface. This intensity correction should range from 0 to 1, negative values indicate that the node should not be drawn. So 0 indicates none of the corresponding colour, 1 indicates fully saturated. Nodes with intensities outside this range should not be used. Note that per colour, gamma corrected edge blending requires three separate intensity scale factors, one for each r,g,b. While this is a simple extension to the format it is not included here and left to the reader to implement if required.

The binary format is a direct representation of the above information. The mesh type and dimensions are stored in the same order as 2 byte unsigned ints, the mesh type can be used to decide whether big or small endian is being used, translators should deal with byte swapping appropriately. The remaining information, 5 values for each node are stored as floating point (4 bytes) each.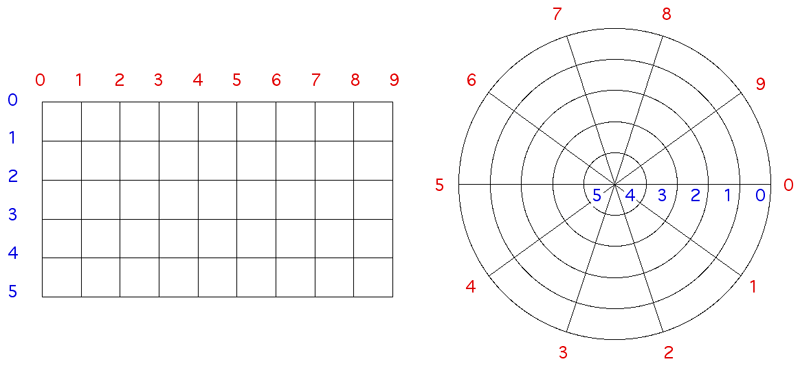

Figure 3. Rectangular and polar mesh topologies, 10x6.
Note that while the mesh appears regular in these examples this is not necessarily
the case, rectangular or polar only indicates the topology and node connectivity.

An example of a mesh file (ascii format) is given here (xyuv.txt). It is rectangular (type 2), the mesh dimensions are 40 x 30. This is the mesh used in figure 4. Note that in this case the warping information is contained within the u,v coordinates, the x,y coordinates form a regular grid over the intended 4:3 aspect ratio of the projector.

Fisheye image.

Warping mesh.

Resulting warped image.

Figure 4. Image warping for dome projection using a spherical mirror.
Image from full dome show called "Origins"

Sample code to draw the mesh

Note that triangle meshes can't be used (in a straightforward way at least) because of the possibility of missing mesh cells. This isn't a serious performance concern because the meshes are normally not that large and they would normally reside in a display list. Of course if there are no missing cells then the mesh can be draw as a triangle strip. In this example the camera (orthographic projection) is assumed to be one unit along the z axis looking at the origin. Note that in some case it may be desirable to find the midpoint of each mesh cell and draw triangles, this can be for performance reasons or to get smoother boundaries when there are unused nodes.

   glBegin(GL_QUADS);
   for (i=0;i<nx-1;i++) {
      for (j=0;j<ny-1;j++) {
         if (mesh[i][j].i < 0 || mesh[i+1][j].i < 0 || mesh[i+1][j+1].i < 0 || mesh[i][j+1].i < 0)
            continue;

         glColor3f(mesh[i][j].i,mesh[i][j].i,mesh[i][j].i);
         glTexCoord2f(mesh[i][j].u,mesh[i][j].v);
         glVertex3f(mesh[i][j].x,mesh[i][j].y,0.0);

         glColor3f(mesh[i+1][j].i,mesh[i+1][j].i,mesh[i+1][j].i);
         glTexCoord2f(mesh[i+1][j].u,mesh[i+1][j].v);
         glVertex3f(mesh[i+1][j].x,mesh[i+1][j].y,0.0);

         glColor3f(mesh[i+1][j+1].i,mesh[i+1][j+1].i,mesh[i+1][j+1].i);
         glTexCoord2f(mesh[i+1][j+1].u,mesh[i+1][j+1].v);
         glVertex3f(mesh[i+1][j+1].x,mesh[i+1][j+1].y,0.0);

         glColor3f(mesh[i][j+1].i,mesh[i][j+1].i,mesh[i][j+1].i);
         glTexCoord2f(mesh[i][j+1].u,mesh[i][j+1].v);
         glVertex3f(mesh[i][j+1].x,mesh[i][j+1].y,0.0);

       }
   }
   glEnd();

The code to draw the polar mesh is similar and the same comments above apply.

   glBegin(GL_QUADS);
   for (i=0;i<nx;i++) {
      for (j=0;j<ny-1;j++) {
         i2 = (i+1) % nx; // Wrap around, i = nx = 0

         if (mesh[i][j].i < 0 || mesh[i2][j].i < 0 || mesh[i2][j+1].i < 0 || mesh[i][j+1].i < 0)
            continue;

         glColor3f(mesh[i][j].i,mesh[i][j].i,mesh[i][j].i);
         glTexCoord2f(mesh[i][j].u,mesh[i][j].v);
         glVertex3f(mesh[i][j].x,mesh[i][j].y,0.0);

         glColor3f(mesh[i2][j].i,mesh[i2][j].i,mesh[i2][j].i);
         glTexCoord2f(mesh[i2][j].u,mesh[i2][j].v);
         glVertex3f(mesh[i2][j].x,mesh[i2][j].y,0.0);

         glColor3f(mesh[i2][j+1].i,mesh[i2][j+1].i,mesh[i2][j+1].i);
         glTexCoord2f(mesh[i2][j+1].u,mesh[i2][j+1].v);
         glVertex3f(mesh[i2][j+1].x,mesh[i2][j+1].y,0.0);

         glColor3f(mesh[i2][j+1].i,mesh[i2][j+1].i,mesh[i2][j+1].i);
         glTexCoord2f(mesh[i2][j+1].u,mesh[i2][j+1].v);
         glVertex3f(mesh[i2][j+1].x,mesh[i2][j+1].y,0.0);

      }
   }
   glEnd();

For prewarping or off-line warping where images are permanently warped (eg: for movie playback) the usual approach is to find the mesh cell for each pixel (x,y) in the final image. The exact (u,v) coordinate is estimated by linear interpolation across the mesh cell, this (u,v) coordinate gives the desired pixel in the input image. In reality supersampling antialiasing also needs to be applied for the highest quality result.