The following discusses the relative merits of tiling conventional displays in order to achieve a high resolution display. The main use of such displays in visualisation is to be able to see detail as well as the big picture. On a lower resolution display one is required to zoom in to see the detail at which point the context is lost. Similarly, when the whole image is visible the detail is smaller than a single pixel and thus lost.

An intentional design criteria in the installation discussed here was the use of a single computer in order to maximise the support across commercially available software, at the cost of performance compared to using a cluster. This can be partly justified by the expectation of increased graphics performance in time.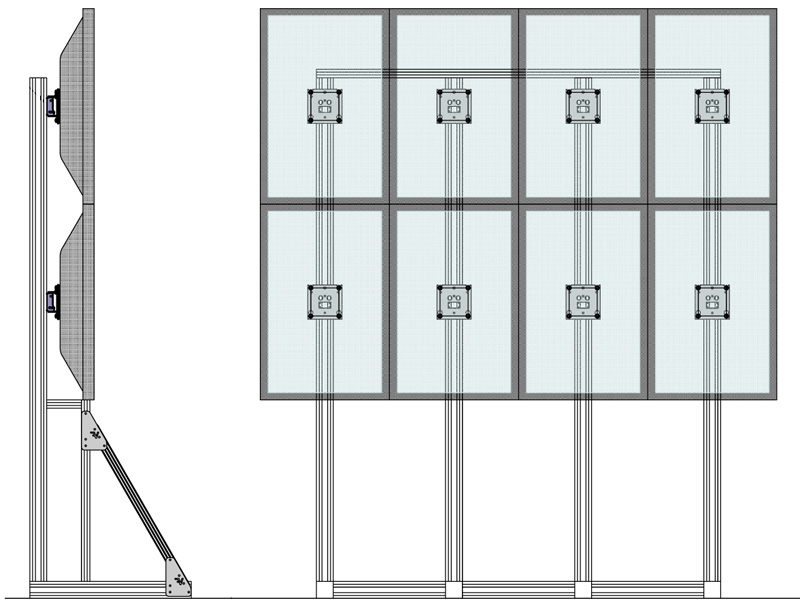

The design is based upon the Apple or DELL 30 inch displays, each one 2560x1600 pixel resolution, the highest on the market at the time. The displays are from the same factory, unfortunately the frame is about the same thickness for both and cannot readily be removed. The DELL displays were chosen simply because of the dark frame vs the lighter frame for the Apple version. The maximum number of dual pipe dual link DVI graphics cards that could be installed in the machine of choice (Apple Mac Pro) was 4, in other words 8 displays. The 2x4 arrangement with the panels on their sides gives the most convenient aspect ratio of 5:4 (6400 x 5120).

While the gaps between each frame is an obvious disadvantage, in order to achieve the raw pixel resolution it is more cost effective than using tiled data projectors. Not only is there the cost benefit but also the software complexity dealing with edge blending between tiled projector displays (assuming a seamless display is the target). It should be noted that these 30 inch monitors at 2560x1600 pixels have almost twice the pixels of a HD projector (2560x1600 compared to 1920x1080).

The colour depth of these displays would seem to be better than what one can achieve with data projectors, this includes the black levels. The first two images are fresh from the repaired Hubble Space Telescope, these first offerings at the time of writing were in the range of 3K and 4K square. The total resolution of the display is 4*1600 pixels horizontally by 2*2560 pixels vertically, a total of 6400 by 5120 (32MPixels).

The following image is a high definition photograph of the Boolardy station in West Australia and the site of the ASKAP (Australia Square Kilometer Array Pathfinder), the site of the proposed SKA. The image is 32,000 by 32,000 pixels.

An example of a tiling of high resolution images, courtesy of Florian Fusseis. Notice the second display from the top left is a different colour, this is due to it being a replacement screen where the displays were originally a running sequence of serial numbers. Colour space adjustments on the panels have subsequently been made to create consistent colours across all panels.

A further example from the recent high resolution images from the Hubble Space Telescope.

The above were all using standard Mac applications (eg: PhotoShop and Preview), the main issue with this is the inability to take account of the gaps between the displays giving quite an unnatural sensation as one tracks content between displays. A particularly elegant way to deal with this is the Quartz Visualiser. The following example uses a Quartz Composer composition to display the image, allow the user to scale, pan, and rotate. Quartz Visualiser then takes that are handles the image across the tiled display and automatically adjusts for a user specified interdisplay gap. While perhaps not evident here, the way the image disappears behind the frames between the display area results in a much more believable result, not surprising perhaps since we are accustomed to viewing scenery through frames windows. The only slight complication is that Quartz Visualiser ignores mouse and keyboard IO, this simply means a separate QC composition is created that runs on a separate computer and controls the translation, zooming, and rotation through a network patch. The two QC compositions are provided to give an idea of how this is achieved.

At the time of writing (Snow Leopard 10.6.1) seems to have a number of bugs when it comes to supporting this number of displays. Serious bugs such as the display preferences for arranging the displays runs very slowly and often fails to display the panels at all.

Application to interactive viewing of cosmological simulation data, 15 million points.

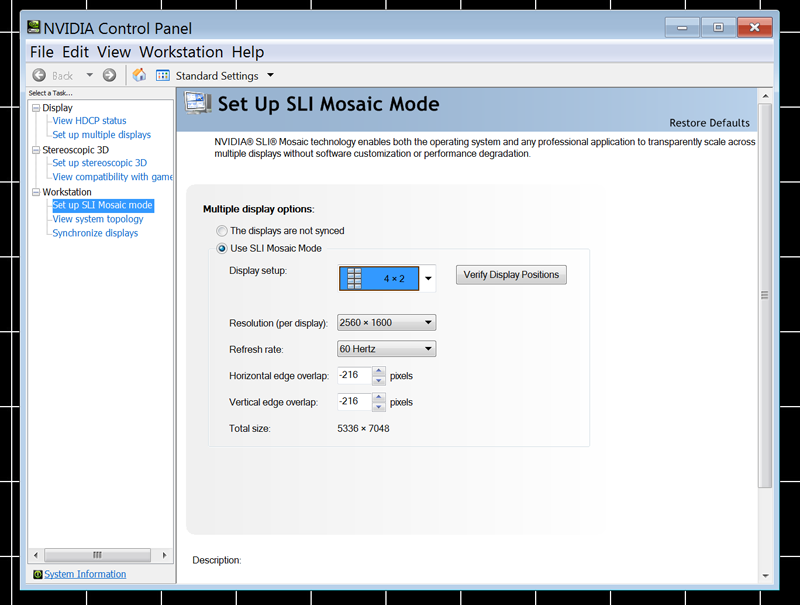
The display has been upgraded from a single Mac with 4 graphics cards to a single MSWindows (and Linux) box with a pair of nVidia Quadraplex units. These, in SLI mode present a single large canvas to any application. The result is a considerable increase in performance while retaining the desired ability to run any software.

Australia

The nVidia drivers take care of the bezel width and in the latest version (at the time of writing) just started supporting portrait mode.

Perth City

This is different to the Google "Liquid Galaxy" on a few points.

• The Liquid Galaxy is "only" 16MPixels whereas this is 33MPixels.

• These panels are aligned flat rather than curved around the users. The curved approach gives a more immersive feeling, this display was targeted more at data visualisation.

• The approach used here is certainly simpler but, depending on what is spent on each Linux box, probably a bit more expensive due to the QuadraPlex boxes.

• As with the OptiPortal system, the Liquid Galaxy is limited in the software it can support.

Mt Cook, New Zealand

Configuration

At the time of writing (February 2011), the nVidia drivers leave a lot to be desired. They don't "naturally" support portrait mode, the work-around is set SLI as a 4x2 landscape and then switch to portrait in the MS display preferences.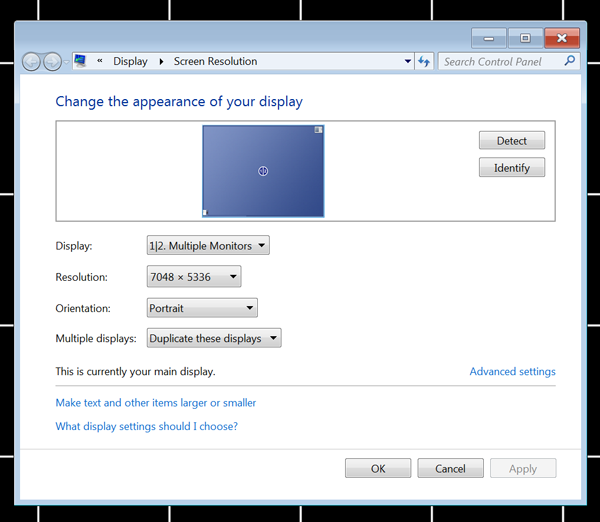

6400 x 5000 pixels	Approximately 12000 x 10000 pixels across the whole image
Approximately 24000 x 20000 pixels across the whole image	Approximately 100000 x 80000 pixels across the whole image

Update: May 2013

This display is made up from lower resolution (just HD, 1920x1080) panels, the obvious difference is the small size of the bezels. Rated at 5.5mm pixel to pixel, in reality it is more like 7mm. The panels used here are from Samsung, each 46 inches diagonal, that is just over 1m wide. The array comes ready to assemble in almost any desired configuration.

Sales pitch: "Such displays can be beneficial when studying high resolution datasets, typically images or high density 2D and 3D graphics. The large number of available pixels allows one to see more of the data thus reducing the need to pan and zoom. The larger physical scale of the display also facilitates collaborative use by more than one person, compared to a single small display."

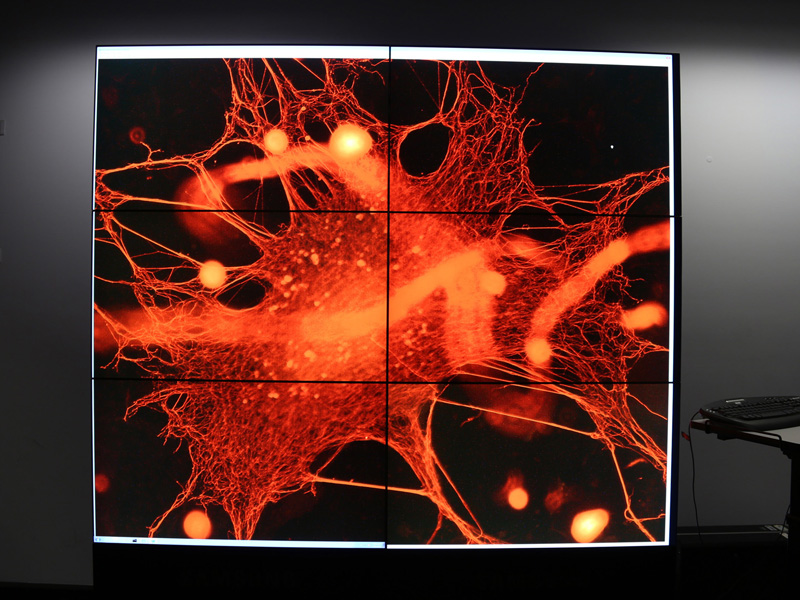
As before, this is driven by a single computer, in this case a FirePro W9000. The unique feature of this card are the 6 DisplayPort outputs allowing one to drive the 6 displays directly. Of course this installation is only about 12 MPixels, much less than the previous version.

AMD control panel shown below, called the "Catalyst Pro Control Centre". Certainly a significantly more stable and elegant interface than the nVidia driver control panels.

The following will present the relative resolution of different displays. A relatively straight forward exercise but as a frequently asked question it warrants some consideration. The first thing to realise is the perceived resolution is not just about the technical resolution of the display or projector. It also depends on the size of the display and the distance of the viewer. The best measure of the perceived resolution is the angle a pixel subtends at the eye, so for a device with a certain number of pixels the perceived resolution increases as the device becomes smaller or as the viewer get closer. In what follows it will be assumed the pixels are square, the vast majority of the cases these days, this allows us to only consider the horizontal angle a pixel subtends at the eye, the vertical angle will be the same. It should be noted that the discussion here assumes a perfect device displaying content with independent pixels, this is rarely the case (see later for degrading effects).

If N is the number of horizontal pixels, W the physical width of the display or projected image, and D the distance the viewer is from the display, then the angle A in radians of a single pixel subtended at the eye is simply

The following table gives some representative subtended angles for commonly encountered display panels or projected images.

What might ask what the resolving power of the human eye is, there is not one definition. 20/20 vision is defined as the ability to resolve two points of light separated by a visual angle of 0.016 degrees. Alternatively the maximum angular resolution of the human eye at a distance of 1 km is typically 30 to 60cm, this gives an angular resolution of between 0.02 to 0.03 degrees.

It should be noted that the above considerations relate to the idealised situation, in reality the actual perceived resolution of a digital image presentation can be less. Some factors reducing the effective resolution are listed below.

• The lens quality of a projector based display.

• The screen door effect around pixels of a display panel or projector.

• Lossy compression of the digital movies being presented, most notably compression such as mpg, H264, and similar. To a lesser extent lossy compression of image formats such as JPEG.

• For projected images the projection surface can degrade the image quality. Similarly for panels the layers of transparent glass/plexiglass in front of the raw pixels diffuse/scatter some light.

Angles marked on a figure from PQM: A New Quantitative Tool for Evaluating Display Design Options. Software, Electronics, and Mechanical Systems Laboratory 3M Optical Systems Division Jennifer F. Schumacher, John Van Derlofske, Brian Stankiewicz, Dave Lamb, Art Lathrop.

Planetariums domes

One might extend this to planetariums although in this case the true resolution is influenced by other things. In what follows it will be assumed that the rated dome projection is real where in fact it is not, for example the use of the words "4K" and "8k" to refer to dome resolution have no meaning in reality but are purely marketing terms. This is due to the following factors.

• How much edge blending is there? Any edge blending can drastically reduce the resolution across the blend, especially as components drift.

• Planetariums with multiple projectors have image warping (geometry correction) occurring so pixels are no longer independent.

• There are lenses on the projectors with blurring and chromatic error effects increasing towards the rim of the lens, especially so for wide angle or fisheye lenses.

• As mentioned before most, if not all, movie playback in planetariums is done using very lossy codecs, such as mpeg and its variants. As such there is significant degradation occurring that again removes any pixel independence, indeed adds even nastier long range effects.

In the following table it is assumed that the observer is in the center of the dome and located at the spring line (the ideal viewing position). For viewers off center the angle a pixel subtends at the eye increases for the most distant side of the dome and decreases for the close side. Note that in the scenario discussed here the radius of the dome is not a factor, on a larger dome the pixels are larger but further away so the perceived resolution remains the same.

Introduction

360 degree video capture has a long history but with a renewed interest in immersive displays and in particular commodity head mounted displays such as the Oculus, the question is often asked how does one capture video at sufficient resolution. Indeed, what is sufficient resolution? The following will provide one way to evaluate the resolution of various 360 degree video capture devices. It should be pointed out that while an idealised capture system will be considered, that is in practice far from the reality. Some of the factors that further degrade the actual capture quality are listed at the end of this document.

One way to evaluate what resolution one needs is to consider the size of a pixel on the final 360 video frame and what area that covers in the scene. In what follows only resolution in the horizontal axis will be considered, that is, cylindrical projections. Similar arguments can be extended vertically for cameras that capture spherical projections such as the LadyBug range.

Imagine a camera that captures cylindrical or spherical projections with N pixels across, these pixels are spread around the 360 degrees and therefore a single pixels subtends 360/N degrees. One can then project this angle into the world and compute the size of the pixel at different ranges R. The width of a pixel W at range R is then simply:

This then provides an upper limit on the resolving ability for a camera that results in N pixel across 360 degrees. This assumes perfect optics, no sensor noise, no image compression, no multiple camera blending/stitching and a raft of other effect that will limit the effective resolution.

In the following table the pixel width at 2m, 5m and 20m are presented for various 360 camera solutions. Please note that the optimal resolution of some of these devices is a "best guess" or based upon manufacturers specifications (often dubious).

Confounding factors

In the above it has been assumed that if a device can capture N pixels horizontally, then those pixels are "pure", this is never the case. Further degradation can occur and some sources are listed below.

• Many of the camera solution do not result in a uniform resolution across the cylindrical or spherical projection. This is particularly true of single camera solutions based upon conical mirrors.

• In the case of many commodity devices, while they may contain the same sensor as more expensive versions, there can be a poorer quality lens in front of the sensor. This generally means that pixels are no longer independent (they receive light over a wider region of the world) and generally an increase in chromatic error. This is particularly true of many of the mobile phone based options.

• Different sensors have different levels of random noise, especially in low light.

• Digital video capture is often limited by the bandwidth to the recording device. To maintain a recording resolution and frame rate the video is generally compressed with corresponding artefacts. The slower the recording device, the more compression and video degradation that occurs. Particularly so with SD storage medium in the GoPro, and others.

• While the only scalable means of increasing the resolution is to use multiple cameras, this introduces potential resolution degradation across the overlap and blending zone. While there are multiple camera configurations, that with the use of mirrors, can create a single projection point, the majority have an offset projection point. For very fundamental reasons this means that a perfect stitch/blend across all depths is impossible.

The resolution of a digital display is a key component of the perceived quality. There are a number of factors that affect the resolution, such as: projector lens quality, interpixel leakage, surface properties, compression codes, geometry distortion, keystone, colour space, and so on. However one can calculate the upper quality possible by the display system by assuming a perfect system where the above have no degrading effect and considering just the pixel resolution. The figure of merit proposed is the angle a pixel subtends at the eye, convenient units for the scale of most current displays is arc seconds. This definition of resolution for some common devices is shown in the chart below, there is a bias/interest in displays the author has been involved in.

Display type	Projection resolution	Dimensions	Viewing distance	Resolution (arc seconds)
Apple 30" display	2560x1600	30 inch diagonal	600mm	86
Standard 17" display	1280x1024	17 inch diagonal	600mm	92
iPod video	320x240	2.5 inch diagonal	300mm	109
Flat screen projection (VROOM)	XGA (1024x768) projector	2m wide	2m	201
Flat screen projection	SXGA+ (1400x1050) projector	2m wide	2m	149
Flat screen projection	HD (1920x1080) projector	2m wide	2m	109
Dome	Full fisheye, XGA (1024x768) projector	*	Located at center	539
Dome	Full fisheye, SXGA+ (1400x1050) projector	*	Located at center	395
Dome	Truncated fisheye, SXGA+ (1400x1050) projector 75% coverage	*	Located at center	292
Dome	Truncated fisheye, HD (1920x1080) projector 56% coverage	*	Located at center	218
Dome	Spherical mirror** and HD (1920x1080) projector Full dome coverage and 2/3 of the pixels used	*	Located at center	309
Dome	Spherical mirror** and HD (1920x1080) projector 80% dome coverage and 3/4 of the pixels used	*	Located at center	264
Dome (planetarium)	6 projectors, each SXGA+ (1400x1050) Assume each projector contributes 2/3 of its pixels to the final image	*	Located at center	149
Dome (planetarium)	6 projectors, each HD (1920x1080) Assume each projector contributes 2/3 of its pixels to the final image	*	Located at center	126
Dome (planetarium)	Full dome using two SONY 4kx2k projectors	*	Located at center	103
Cylinder (AVIE)	6 projectors, each SXGA+ (1400x1050) Assume 200 pixel edgeblend	*	Located at center	178
Neptune			From Earth	2.5
Mars			From Earth	20

Notes

• ^*For the dome and cylindrical environments the resolution is independent of the size of the display assuming the observer is at the central sweet spot. As the dimensions of the surface get larger the observer gets further away.

• For the multiple projector domes it is assumed that 2/3 of the display area of each projector contributes to the final image. This does depend on the aspect ratio of the projectors being used but is the upper limit for standard geometry corrected and edge blended frames.

• ^**The spherical mirror projection does not result in equal size pixels across the dome and it is possible to vary the dome coverage from the same as a truncated fisheye to 100%. Some parts of the dome will be higher resolution, others lower.

In what follows the following symbols are used.
x y are the physical linear dimensions, width and height
r is the radius
w h are the pixel dimensions, width and height
d is the viewing distance
n is the number of projectors

A small angle approximation is used, namely tan(x) = x for small values of x.

Planar display, single projector

If the pixels are square and all are used then this reduces to

Cylindrical display
Take the edge blend width in pixels into account for "w", the pixel width of each projector.

If the viewer is standing in the center this reduces to

Multiprojector Dome eg: planetarium
Assume each projector contributes 2/3 of its pixels to the final image.

If the viewer is located in the center then this reduces to

Dome projection with a single full fisheye

For the observer at the center of the dome this reduces to

Dome projection with a 3/4 truncated fisheye

For the observer at the center of the dome this reduces to

Dome projection using a single projector and spherical mirror

Assume p% of the pixels end up on the dome that is q% covered.

For the observer at the center of the dome this reduces to