Field of view and focal lengthWritten by Paul BourkeApril 2003
Camera and photography people tend to talk about lens characteristics in terms of "focal distance" while those involved in synthetic image generator (such as raytracing) tend to think in terms of field of view for a pinhole camera model. The following discusses (an idealised at least) way to estimate the field of from the focal distance. view The focal length of a lens is an inherent property of the lens, it is the distance from the center of the lens to the point at which objects at infinity focus. Note: this is referred to as a rectilinear lens. 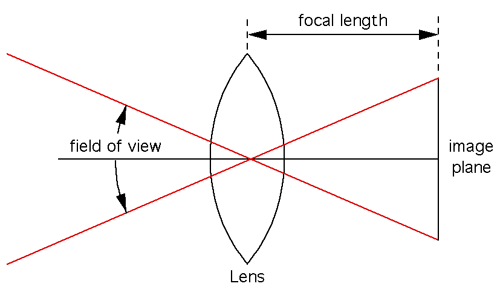
That there are three possible ways to measure field of view: horizontally, vertically, or diagonally. The horizontal field of view will be used here, the other two can be derived from this. From the figure above, simple geometry gives the horizontal field of view where "width" is the horizontal width of the sensor (projection plane). So for example, for a 35mm film (frame is 24mm x 36mm), and a 20mm (focal length) lens, the horizontal FOV would be almost 84 degrees (vertical FOV of 62 degrees). The above formula can similarly be used to calculate the vertical FOV using the vertical height of the film area, namely: So for example, for 120mm medium format film (height 56mm) and the same 20mm focal length lens as above, the vertical field of view is about 109 degrees.
Changing to/from vertical/horizontal field of viewWritten by Paul BourkeMarch 2000 See also: Field of view and focal length
PovRay measures its field of view (FOV) in the horizontal direction, that is, a camera FOV of 60 is the horizontal field of view. Some other packages (for example OpenGL gluPerspective()) measure their FOV vertically. When converting camera settings from these other applications one needs to compute the corresponding horizontal FOV if one wants the views to match. It isn't difficult, here's the solution. By calculating the distance from the camera to the center of the screen one gets the following: Solving this gives
Or going the other way
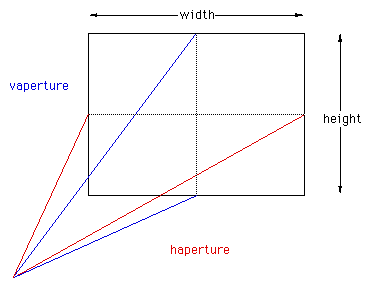
Where width and height are the dimensions of the screen. For example, a camera specification to match an OpenGL camera FOV of 60 degrees might be:
camera {
location <200,3600,4000>
up y
right -width*x/height
angle 60*1.25293
sky <0,1,0>
look_at <200+10000*cos(-clock),3600+2500,4000+10000*sin(-clock)>
}
Lens Depth of FieldWritten by Paul BourkeJune 2005 The depth of field of a lens is given by the following expression where "F" is the F-stop value, "d" is the distance to the subject from the sensor plane, "c" is the circle of confusion taken here to be the width of a pixel on the sensor, and "f" is the focal length of the lens. 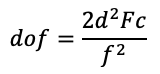
Things that follow directly from the equation
Worked example: Canon R5 (full frame), 50mm lens, F11 and distance of 10m.
Lens Correction and DistortionWritten by Paul BourkeApril 2002
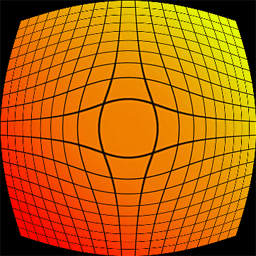
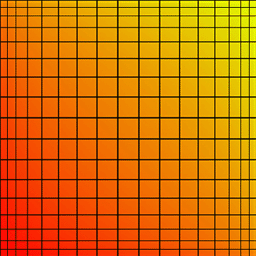
The following describes how to transform a standard lens distorted image into what one would get with a perfect perspective projection (pin-hole camera). Alternatively it can be used to turn a perspective projection into what one would get with a lens. To illustrate the type of distortion involved consider a reference grid, with a 35mm lens it would look something line the image on the left, a traditional perspective projection would look like the image on the right.
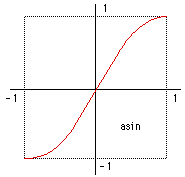
The equation that corrects (approximately) for the curvature of an idealised lens is below. For many lens projections ax and ay will be the same, or at least related by the image width to height ratio (also taking the pixel width to height relationship into account if they aren't square). The more lens curvature the greater the constants ax and ay will be, typical value are between 0 (no correction) and 0.1 (wide angle lens). The "||" notation indicates the modulus of a vector, compared to "|" which is absolute value of a scalar. The vector quantities are shown in red, this is more important for the reverse equation. 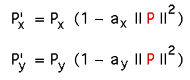
Note that this is a radial distortion correction. The matching reverse transform that turns a perspective image into one with lens curvature is, to a first approximation, as follows. 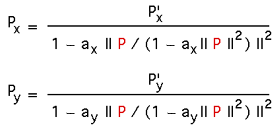
In practice if one is correcting a lens distorted image then one actually wants to use the reverse transform. This is because one doesn't normally transform the source pixels to the destination image but rather one wants to find the corresponding pixel in the source image for each pixel in the destination image. Note that in the above expression it is assumed one converts the image to a normalised (-1 to 1) coordinate system in both axes.
Example code "Proof of concept code" is given here: map.c As with all image processing/transformation processes one must perform anti-aliasing. A simple super-sampling scheme is used in the above code, a better more efficient approach would be to include bi-cubic interpolation. Adding distortionThe effect of adding lens distortion to the image is shown below for a perspective projection of a Menger sponge by Angelo Pesce. The image on the left is the original from PovRay, the image on the right is the lens affected version. (distort.c)
References
F. Devernay and O. Faugeras.
SPIE Conference on investigative and trial image processing.
SanDiego, CA, 1995.
Automatic calibration and removal of distortion from scenes of structured environments.
H. Farid and A.C. Popescu.
Journal of the Optical Society of America, 2001.
Blind removal of Lens Distortion
R. Swaminatha and S.K. Nayer.
IEEE Conference on computer Vision and pattern recognition, pp 413, 1999.
Non-metric calibration of wide angle lenses and poly-cameras
G. Taubin.
Lecture notes EE-148, 3D Photography, Caltech, 2001.
Camera model for triangulation
Non-linear Lens DistortionWith an example using OpenGL (lens.c, lens.h)
Written by Paul Bourke
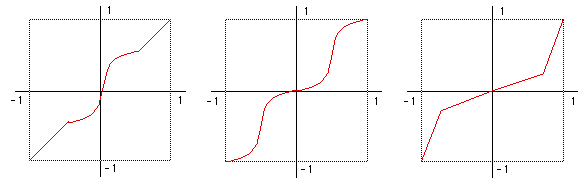
The following illustrates a method of forming arbitrary non linear lens distortions. It is straightforward to apply this technique to any image or 3D rendering, examples will be given here for a few mathematical distortion functions but the approach can use any function, the effects are limited only by your imagination. At the end an OpenGL application is given that implements the technique in real-time (given suitable OpenGL hardware and texture memory).
Notes on resolution Some parts of the image are compressed and other parts inflated, the inflated regions need a higher input image resolution in order to be represented without aliasing effects. The above transformations cope with the input and output images being different sizes, normally the input image needs to be much larger than the output image. To minimise aliasing the input image should be larger by a factor equal to the maximum slope of the distorting function. There are no noticeable artefacts in these example because the input image was 10 times larger than the output image. OpenGL
This OpenGL example implements the distortion functions above
and distorts a grid and a model of a pulsar. It can readily be modified
to distort any geometry. The guts of the algorithm can be found in the
HandleDisplay() function. It renders the geometry as normal, then copies the
resulting image and uses it as a texture that is applied to a regular
grid. The texture coordinates of this grid are formed to give the
appropriate distortion.
(lens.c, lens.h)
The left button rotates the camera around the model, the middle button
rolls the camera, the right button brings up a few menus for changing the
model and the distortion type. It should be quite easy for you to add
your own geometry and to experiment with other distortion functions.
Feedback from Daniel Vogel One thing you might want to consider is using glCopyTexSubImage2D instead of doing a slow glReadPixels. Using the first allows me to play UT smoothly with distortion enabled. glReadPixels is a very slow operation on consumer level boards. And until there is a "rendering to texture" extension for OpenGL taking the texture directly from the back buffer is the fastest way - and it even is optimized.
Computer Generated Camera Projections and Lens DistortionWritten by Paul BourkeSeptember 1992 See also Projection types in PovRay
Most users of 3D modelling and rendering software are familiar with parallel and perspective projections when they generate wire frame, hiddenline, simple shaded or highly realistic rendered images. It is possible to mathematically describe many other projections some of which may not be available, feasible, or even possible with conventional photographic equipment. Some of these techniques will be illustrated and discussed here using as an example a computer based model of Adolf Loos' Karntner bar. The 3D model was created by Matiu Carr in 1992 at the University of Auckland's School of Architecture, using Radiance.
The following is a 180 degree (vertically) by 360 degree (horizontally) angular fisheye. It unwraps a strip around the projection sphere onto a rectangular area on the image plane. The distance from the centre of the image is proportional to the angle from the viewing direction vector.  Figure: Fisheye 180
90 degree (vertically) by 180 degree (horizontally) angular fisheye.  Figure: Fisheye 90
A panoramic view is another method of creating a 360 degree view, it removes vertical bending but introduces other forms of distortion. This is created by using a virtual camera that has a 90 degree vertical field of view and a 2 degree horizontal field of view. The virtual camera is rotated about the vertical axis in 2 degree steps, the resulting 180 image strips are pasted together to form the following image.  Figure: Panoramic 360 Some other "real" examples
 180 degree panoramic view of Auckland Harbour.
 360 by 180 degree panoramic view created by a camera developed at Monash University, Melbourne. | ||||||||||||||||||||||||||||||||