Toward an Integrated Continuum Model of Cerebral Dynamics: The Cerebral Rhythms, Synchronous Oscillation and Cortical Stability.Journal of Biological and Information Processing Sciences, Volume 63, Issue 1-3, pp 71-88, December 2001.Doi: 10.1016/S0303-2647(01)00148-4
C.L Chapman1, N. Hawthorn1,4, G.J Lees4, D. Alexander1
Keywords:
Continuum models of cerebral cortex with parameters derived from physiological data, provide explanations of the cerebral rhythms, synchronous oscillation, and autonomous cortical activity in the gamma frequency range, and suggest possible mechanisms for dynamic self-organisation in the brain. Dispersion relations and derivations of power spectral response for the models, show that a low frequency resonant mode and associated travelling wave solutions of the models' equations of state can account for the predominant 1/f spectral content of the electroencephalogram (EEG). Large scale activity in the alpha, beta, and gamma bands, is accounted for by thalamocortical interaction, under regulation by diffuse cortical excitation. System impulse responses can be used to model Event-Related Potentials. Further classes of local resonance may be generated by rapid negative feedbacks at active synapses. Activity in the gamma band around 40 Hz, associated with large amplitude oscillations of pulse density, appears at higher levels of cortical activation, and is unstable unless compensated by synaptic feedbacks. Control of cortical stability by synaptic feedbacks offers a partial account of the regulation of autonomous activity within the cortex. Synchronous oscillation occurs between concurrently excited cortical sites, and can be explained by analysis of wave motion radiating from each of the co-active sites. These models are suitable for the introduction of learning rules - most notably the coherent infomax rule. 1. Introduction.The operation of the brain requires the coordinated interplay of billions of neurones via their synapto-dendritic couplings. The development of a concise mathematical description of this interplay is a major goal of neuroscience, but attempts to attain this goal encounter problems of a fundamental nature. What are the essential cellular properties needed to account for the local cell pulse characteristics, and the macroscopic fields (notably the electroencephalogram (EEG)) emitted by the working brain? How are the observable pulses and fields related to information processing in the brain? Which are the essential features of the brain's gross anatomy which need to be taken into consideration? How do the dynamics of neurones interact with growth and other plastic modifications, to enable adaptative learning? Accounts of interactions within populations of neurones have generally utilised neural network methods, in which the elementary units considered are the neurones (eg, Amit et al 1990; Arbib et al 1998; Traub et al 1996; Whittington et al 1995; Lumer et al 1997a,b; Wilson and Bower 1991). Despite their many virtues, such models are limited by the rapid increase in their numerical complexity as the scale and detail of simulation is increased. This complexity also generally makes them unsuited to mathematical analysis. This paper describes the current attempts being made by our group to account for the dynamics of the brain in as simple a way as possible. We utilise continuum modelling methods pioneered in the works of Freeman (1975), Wilson and Cowan (1973), Nunez (1981, 1995) , Lopes da Silva (van Rotterdam et al 1982 and subsequent), Haken (eg, Jirsa and Haken 1996), Zhadin (1994) and others. Our work has been guided also by the following principles:
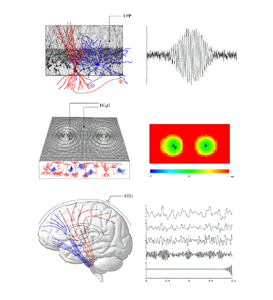
Figure 1 shows the basic aspects of the brain's operation we seek to analyse. Three principal scales of organisation need to be considered. Firstly, at the microscopic scale in any locale of cortex, local interactions between a mixed population of excitatory and inhibitory cells take place. Interactions are largely mediated by fast neurotransmitters. The existence of synaptic and dendritic delays, and synapto-dendritic feedbacks, means that local oscillations of mean dendritic potential and pulse density are likely in response to any perturbation. The properties of such local oscillation determine the signal transfer characteristics and attractor dynamics exhibited by local neural networks. Secondly, at a scale from fractions of a millimeter to many centimeters of cortex, patches of active cells have been experimentally observed to enter into synchronous oscillation. That is, cross-correlations of pulse density, or of mean local field potential at the separated locii are maximal at zero lag. This phenomena has been widely, although controversially, considered to act as a substrate for association processes in the cortex. (eg, Eckhorn et al 1998; Singer 1994; Singer and Gray 1995; Stryker 1989; Bressler et al 1993; Livingston 1996; Miltner et al 1999; Neuenschwander and Singer 1996; Palm and Wennekers 1997; Steriade et al 1996; Gray and Singer 1989; Gray et al 1989). Such interactions depend particularly upon excitatory cortico- cortical fibres of medium to large scale. Thirdly, at the scale of the whole brain, the total cortical system interacts with the subcortical systems. These interactions include reciprocal interactions of thalamus and cortex, and limbic and cortical projections to the basal ganglia and elsewhere. These descending pathways ultimately exert return controls via the reticular arousal system and related fibres, back upon the cortex (eg Steriade et al 1990; Alexander et al 1990; Posner and Petersen 1990). By these means the cortex is capable of self-control of both its mean level of activity (cortical arousal) and spatial pattern of activity (an aspect of attention), as indirectly observed experimentally (eg, Gevins et al 1983; Munk et al 1996; John et al 1969; Walter et al 1967; Xu et al 1997). 3. State equations
Figure 2 summarises the elementary physiological properties considered basic in our recent models, and their mathematical expression (Robinson et al 1997, 1998a,b; Rennie et al 1999, 2000a; Wright 1999; Wright et al 2000). A field of mixed excitatory and inhibitory neurones are considered as a continuum approximating the cortex in two dimensions. The control parameter for cortical activity is the diffuse excitation delivered by the reticular formation of the brain stem. The response of dendritic membranes to synaptic inputs is nonlinear, because of the influences of reversal potentials, Rqp. Thus the gross post synaptic potential (PSP size) is a function of afferent synaptic inputs, modified by reversal potentials and further synaptic feedback processes, which may be included in the term H(t). The time course of average dendritic potentials (the PSP shape, as measured at the neuronal soma) is modelled by a biexponential function with fixed time constants, alpha and beta. Mean soma potential, V, (considered linearly proportional to the population local field potential) is related to mean efferent pulse rate, Q, by a sigmoidal function which takes its form from the distribution of cell action potential thresholds. The propagation of action potentials in the continuum of surrounding neurones is expressed as a linear wave equation, which relates afferent and efferent pulses in time and space, and a spatial damping term, gamma. Gamma is determined by the velocity of axonal conduction and the geometry of axonal projections. Inhibitory cells we have for the most part considered as wholly local in their action, with long range cortical interactions occurring by excitatory connections. To these basic state equations we have subsequently added consideration of co-resonance of cortex with the thalamic system (Robinson et al 2000), and more complex feedback processes operating at synaptic level, as will be discussed in later sections. The basic state equations enable direct calculation of steady state fixed points for the system, dispersion relations for the medium, and the power spectrum of local field potential (EEG) in response to white noise inputs. They also permit simulation of an extended field of cortex, enabling inspection of time series and spatial properties of activity in the medium. 4. Parameters
Table 1 lists the basic parameters of the state equations, with current values applied in our work. Values for these parameters have been obtained largely from the work of Braitenberg and Schuz, Thomson et al, Liley and Wright, and Rennie et al, cited in the introduction. There is some sensitivity of emergent system properties, even with parameter variation within the approximate physiological range. To aid in melding cellular physiological parameters with experimental observations on EEG, we have partly relied upon initial numerical simulations with a nondimensional model (eg,Wright 1999) and partly upon analytical explorations of the basic state equations (Robinson et al 1998a; Rennie et al 1999) Parameters have been subsequently set with some "tuning" within the physiological range, so as to better fit observed EEG frequencies, etc (Rennie et al 2000a). 5. Microscopic dynamicsFigure 3 shows the roots of dispersion relations calculated from our basic state equations, with the parameter values listed in table 1 (Rennie et al 2000a). Dispersion relations encapsulate the system's favoured modes of resonance when driven by white noise inputs, and thus act as an analytic adjunct to numerical simulations. Resonance occurs at specific combinations of frequency and wavenumber. Frequency of resonance (omega) is measured by the horizontal distance of a root from the origin. Temporal damping is estimated by the value on the imaginary axis. Shown here are only those roots which are relatively lightly damped. For each root the squares show the resonance associated with a wavenumber (k) of zero, and the tails indicate the root values as wavenumber increases. The two cases shown are those obtained for relatively low (10/s) and relatively high (350/s) input pulse rates of cortical activation delivered by the nonspecific reticular activation system. Two relatively lightly damped roots are apparent - a low frequency resonance at k=0, which is also associated with a travelling wave system, and a high frequency resonance which becomes less damped as cortical activation is increased, until it becomes unstable, as indicated by the root's placement above the horizontal (real) axis. These two roots give rise to spectral content of 1/f character, and activity associated with a sharp spectral peak in the gamma range (around 40Hz +), respectively. The occurrence of a potentially unstable root in the gamma range immediately suggests a basis for autonomous cortical activity at this frequency range. This is in keeping with the many experiments on synchronous oscillation cited in section 2, which reveal powerful local pulse and local field potential oscillations around this frequency, during processing of inputs. Obviously, sustained unstable activity as illustrated in figure 3, is unphysiological. For this reason we are presently modifying the basic state equations to include negative feedbacks at synaptic junctions. Table 2 lists some of the more prominent of the factors known to modify synaptic neurotransmission. Of particular importance in this context are the fast feedbacks, operating in the 1-5 ms time range. These complement the fast negative feedback actions induced by membrane reversal potentials. Probably the dominant fast effect of this type arises from the post-synaptic activation and deactivation of glutamate receptors (eg, Tones and Westbrook 1996). When fast negative feedbacks are introduced to the basic state equations, two major influences on system dynamics are apparent. Firstly, synaptic feedbacks can introduce local resonances. Figure 4 shows time series and power spectra associated with increasing cortical activation in the presence of one kind of fast inhibitory feedback. Similar patterns of resonance also arise when strong negative feedback is present at excitatory synapses. It can be seen that as cortical activation increases (down figure 4) EEG-like activity appears which exhibits multiple peaks in the power spectrum, progressively moving to higher frequencies, approximately imitating activity in the the theta, alpha, beta, and gamma bands. At sufficiently high cortical activation runaway unstable activity, in the 40 Hz range, appears. These results were obtained from our non-dimensional model (Wright 1999). The values of the parameters in this version have been tuned to optimise the resemblance to EEG. Although preliminary, these results serve to show that rapid synaptic feedbacks enhance local resonances not apparent as lightly damped roots in the basic state equations. Thus resonances in the EEG range, including resonances near the frequencies of the great cerebral rhythms, may arise locally within the cortex, as a consequence of synaptic feedbacks. As will be discussed in section 7 the major cerebral rhythms can be quantitatively well accounted for at macroscopic scale, by cortico-thalamic mechanisms. There is thus no need to appeal to local cortical low-frequency resonances, to account for macroscopic EEG in the sub-gamma range. But co-resonance of microscopic and macroscopic neuronal fields is an implied mechanism for interaction between scales, in our models. Secondly, sufficiently strong negative feedback operating at excitatory synapses, or positive feedback at inhibitory synapses, or various combinations, can act as a time-varying control upon otherwise unstable resonance in the gamma range. With appropriate choice of the time constants of these feedbacks, autonomous generation of activity develops, yet remains locally controlled at pulse rates within the physiological range. To illustrate the impact of this feedback control, figure 5 shows snapshots from a small scale cortical simulation which includes first approximations to these strong synaptic feedbacks. The continuous emergent activity invites comparison to the dynamics within the gamma range of spontaneously firing pools of neurones, in which bursting patterns of action potentials are observed. Chaotic and limit cycle types of activity may be present within various basins of attraction, but as of yet little work on their classification has been undertaken. In contrast, at lower levels of cortical activation, only point attractors are present. 6. Synchronous oscillation - mesoscopic interactions at longer range.During the development of these simulations it became apparent that synchronous oscillation, with close analogy to that observed physiologically appeared as a property of the simulations without any additional assumptions (Wright 1997a). We have since developed analytical and numerical treatments of zero-lag cross correlation (Robinson et al 1998a, Chapman et al 2000), and matched the phenomenon we observe to some physiological results (Wright et al 2000). The following account of synchronous oscillation applies to all frequencies, but, as is the case in physiological experiments, large oscillations in the gamma band, at about 40 Hz, are associated with the largest amplitudes, and occur when the cortex is excited by higher levels of input. If two points on the simulated cortical surface are driven by separate, completely uncorrelated, inputs (or if uncorrelated autonomous local cortical activity emerges at two seperated points) then, within a few milliseconds cross-correlated activity, maximal at zero lag, appears in the neighbourhood of both active sites. For this effect to occur, the two points must be relatively strongly coupled, and axonal delay must be small compared to the rise and fall time of the dendritic response. The speed of onset depends mainly on the axonal delay. This effect does not depend upon system nonlinearity , as is frequently assumed by those familiar with stochastic resonance in other situations. It is instead associated with linear wave transmission in the simulated cortex. Figure 6 sums up our current understanding of the mechanism of synchronous oscillation. In the top frames of figure 6 it can be seen how a large field of zero-lag synchrony surrounds both sites of uncorrelated input. In the middle frames eigenmode decomposition shows that the first eigenmode of the wave activity radiating from both driven sites is predominant, and this eigenmode defines the field of synchrony. The bottom frames attempt to convey the essence of the physical process, and can be explained as follows: The uncorrelated inputs can be decomposed into their even and odd components roughly, the parts of each driving signal which are in phase with the other, and those parts of reversed phase. Wave activity radiates from both sites as outwardly propagating, dissipative, linear waves, creating a small local field of "self-synchrony" about each site, by the summation of signals transmitted by pathways of similar lag. The travelling waves obey simple superposition rules subject to dissipation - but interactions of afferent signals at summing junctions (dendrites) in the surrounding field dissipate even and odd components in their inputs selectively. Even components reinforce one another, while odd components tend to cancel about the signal mean. Thus, in the field of both driven sites, the activity induced by the even components in the driving signals dominates, and a field of zero-lag correlated activity emerges as the first eigenmode of the wave activity. It can be shown that the magnitude of this zero-lag correlated field is sensitive to dendritic delay time, axonal conduction lag between sites, and the relative strengths of couplings in the field. Figure 7 gives an example of how the results produced in simulation can be made to qualitatively reproduce those seen in physiological experiments on synchronous oscillation (Wright et al 2000). Cross-correlation of pulses from a pair of recording sites is greatest when the stimulus is a single large bar, next for two smaller bars moving in the same direction, and least for smaller bars moving in opposite directions. We believe the match to experimental data might be rendered quantitatively precise if relative coupling strengths, coherence within signals in the input pathways, and strengths of overlying noise, were more closely matched between simulation and experiment. 7. The macroscopic EEG field. A thalamo-cortical resonance model.When spectral responses of the simulations applied in figures 4 and 5 are compared to the spectral content of the macroscopic EEG, the simulations prove to be inadequate with regard to both relative amplitude and width of spectral peaks. A purely cortical account ignores the role long ascribed to thalamic sources in generation of the EEG - to which other models of the alpha rhythm have been directed - notably that of van Rotterdam et al (1982). On the other hand no models attempting to account for the origin of the cerebral rhythms have been able at the same time to account for the predominant background 1/f spectral content of EEG and magnetoencephalogram (Novikov et al 1997). It turns out that the addition of a simple feedback loop to the basic state equations, while retaining parameters close to those listed in table 1, gives a good account of the entire macroscopic EEG spectrum over low to high levels of cortical activation (Robinson et al 2000). The loop time required is consistent with an interaction between cortex and a subcortical system (assumed to be the thalamus) with a synapto-dendritic delay appropriate for 1-2 synapses. The background 1/f1 spectral content of EEG at low frequencies, with a "knee" around 15 Hz above which power decays as 1/f5, is well accounted for by the low frequency root system, similar to that seen in figure 3. The thalamocortical resonance then accounts for the occurrence of spectral peaks at the alpha, beta, and gamma ranges, as shown in figure 8. These resonances are associated with low wavenumbers and can be thought of as global resonances, as opposed to the local resonances associated with fast synaptic feedback described in section 5. We have found that the spectral progression with increasing cortical activation is well fitted by this model, for all experimental data obtained over a wide variety of states of cortical activation, from sleep to high alerting. These results will be later reported (Robinson et al, in preparation). Finally it can be observed that the thalamocortical spectral model also permits the simulation of the cortical event related potential (ERP), by treating the ERP as the cortical impulse response to brief sensory stimuli, with subsequent modulations imposed by the cortex upon the cortico-thalamic resonance (Rennie et al 2000b). Examples are shown in figure 9. These serve to emphasise that a fuller account of cortical dynamics must take into account interactions of cortex with subcortical systems, over a multitude of pathways. 8. Some wider implications.
The classes of dynamics seen in our models suggest the prospect of a future unification of brain dynamic models with some aspects of computational and information-theoretic approaches to understanding brain function. * "Edge of chaos" and universal computation, versus locally autonomous firing and synchronous oscillations in the gamma range. In several controversial papers Langton (1986, 1990) has drawn upon the work of Wolfram (1984) and von Neumann (1949) to propose that physical systems undergoing local second- order phase transitions may include universal computation as a potential property. Such systems exhibit prolonged transitional states, and have been termed "edge of chaos". Langton has suggested the brain may exploit the "edge of chaos" to achieve cognition, in ways he has not stated in physiological terms. In conformity with this suggestion, local phase transitions in the gamma band are implied by our findings. With these local transitions stabilised in the large by rapid synaptic feedbacks and/or adiabatic actions of slower neurotransmitters and polysynaptic cortical- subcortical interactions, the regulation of cerebral phase transitions on all spatio-temporal scales is implicit. * Cortical dynamics, coherent infomax and storage of information in cortical networks. Kay and Phillips (1997) and Phillips and Singer (1997) have described a learning rule related to the Hebb principle, which they believe is physiologically realistic and which exploits the occurrence in the brain of synchronous oscillation. Synchrony between separate sites of input in an abstract passive-filter neural network is imposed by assuming the existence of hypothetical "Contextual Field" (CF) fibres. The learning rule operates to maximise the storage in synaptic connections, of relations among the information streams introduced at separate "Receptor Field" (RF) sites of input. This information storage principle they term "coherent infomax".The physiological validity of the learning rule seems further confirmed by its application to learning of connectivity in models of cortical anatomy (Alexander et al 2000) where we have found this rule more efficient than simpler Hebb formulations in generating realistic visual cortex connectivities. In these simulations of cortical connectivity we have shown that the learning rule results in a mapping of the visual field onto cortex such that the visual field becomes tiled with small homotypic maps of the visual field - each tile about the size of a macrocolumn. This property may explain the way that contextual information is introduced into local cortical information processing (Phillips and Singer 1997; Phillips and Pflieger 1999). Our account of the mechanism of synchronous oscillation appears to obviate the need for the special assumption of CF connections giving rise to synchrony. It can be shown that our model of synchrony can account for the transfer of information about stimulus properties to synapses distributed widely in the cortical field (Wright et al 2000). Further, as indicated in another paper in the Agora Symposium, the 1/f background activity of the less excited cortex may enable optimum information transfer among the active cortical sites, in accord with the coherent infomax requirement that passive- filter information transfer take place between active RF sites. There appears to be no reason why the coherent infomax principle might not include the extraction of informational relations among activity patterns in autonomously active patches of cortex, as well as among discrete external sources of input. (Wright 1997b). That is, locally autonomous, "edge of chaos", attractor dynamics would give rise to an internal type of RF input. These internal RF inputs, and RF inputs from sensory pathways, linked into fields of coherent oscillation by the cortical wave medium would act to store informational relations between RF's of both internal and external origins. Applying these considerations to an imaginary organism interacting with an environment, the coherent infomax rule would thus allow association of environmental stimuli with the organism's internally generated cognitive and motor activity. As the organismıs motor activity, sensory and cognitive activity would all bring about rewarding and punishing reinforcement influences mediated by hard-wired, survival selected, subcortical systems (eg Olds and Milner 1954), we may conjecture that adaptive learning could result. This conjecture depends upon the further assumption that the reward and punishment systems act to preferentially select the synaptic storage of information over appropriate time scales. 9. ConclusionIt appears that a relatively simple set of state equations with parameter values close to those determined by independent physiological measurements, accounts for observed dynamics of cortical neurones at microscopic, mesoscopic and macroscopic scales. At microscopic level, fast synaptic feedbacks appear to be crucial to the stability of the excited cortex. At mesoscopic scale interactions via dissipative wave transmission between excited cortical areas create fields of synchrony, and at macroscopic scale low- frequency resonances and travelling waves generate the 1/f background spectrum of the cortex. When this intracortical dynamic is supplemented by resonance between cortex and thalamus, much of the spectral content of the EEG is accounted for. The emerging picture of cerebral dynamic organisation is different to that envisaged in alternate models - notably those of Nunez (1981) - and much may be gained by future experimental comparison of competing formulations. Our models are testable in a number of ways - for example, we predict dependence upon brain size, axonal conduction velocity and dendritic delays, of the "knee" frequency between 1/f and 1/f5 limbs of the background spectrum. The present work offers the prospect that dynamical brain events taking place across a wide range of scales might be unified within a single account. It also offers the more remote prospect of unification of dynamics with specific learning rules. Whether such a unified account is truly possible should be revealed as progressively greater anatomical and physiological detail, and more exact specifications of parameters are included. As indicated in the text, at the time of writing we are attempting several lines of development of this kind. These include simulations with more realistic anisotropic cortical connectivity at macroscopic and microscopic scales, the simulation of cortical evoked potentials and the improved specification of synaptic feedback mechanisms. References. Alexander, D.M., Bourke, P.D., Sheridan, P., Konstandatos, O., Wright, J.J. 2000. Emergence under Hebbian learning of local maps in the primary visual cortex: Orientation Preference in the Tree Shrew. (in preparation) Alexander, G.E., Crutcher, M.D., DeLong, M.R. 1990. Basal ganglia-thalamocortical circuits: parallel substrates for motor, oculomotor, "prefrontal" and "limbic" functions. In: Uylings, H.B.M., van Eden, C.G., de Bruin, J.P.C., Feenstra, M.G.P. (Eds.), Progress in Brain Research. Elsevier, Amsterdam. Amit, D.J., Evans, M.R., Abeles, M. 1990. Attractor neural networks with biological probe records. Network 1, 381-405. Arbib, M.A., Erdi, P., Szentagothai, J. 1998. Neural Organisation: Structure, Function and Dynamics. MIT Press, Cambridge Mass., London. Braitenberg, V., Schuz, A.1991. Anatomy of the Cortex: Statistics and Geometry. Springer, Berlin. Bressler, S.L., Coppola, R., Nakamura, R. 1993. Episodic multiregional cortical coherence at multiple frequencies during visual task performance. Nature 366,153-156. Chapman, C.L., Bourke, P.D., Wright, J.J. 2000. Spatial eigenmodes and synchronous oscillation: coincidence detection in simulated cerebral cortex. (submitted) Eckhorn, R., Bauer, B., Jordon, W., Brosch, M., Kruse, W., Munk, M., Reitboeck, H.J. 1988. Coherent oscillation: a mechanism of feature linking in visual cortex? Biol. Cybern. 60,121-130. Freeman, W.J. 1975. Mass Action in the Nervous System. Academic Press, New York. Gevins, A.S., Schaffer, R.E., Doyle, J.C., Cuttilo, B.A., Tannehill, R.S., Bressler, S.L. 1983. Shadows of thought: shifting lateralisation of human brain electrical patterns during a brief visuomotor task. Science 220, 97-99. Gray, C.M., Singer, W. 1989. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natn. Acad. Sci. 86, 1698-1702. Gray, C.M., Konig, P., Engel, A.K., Singer, W. 1989. Oscillatory responses in cat visual cortex exhibit intercolumnar synchronisation which reflects global stimulus properties. Nature 388, 334-337. Jirsa, V.K., Haken, H. 1996. Field theory of electromagnetic brain activity. Physical Review Letters 77, 960-963. John, E.R., Shimokochi, M., Bartlett, F. 1969. Neural readout from memory during generalisation. Science 164, 1534-1536. Kay, J. , Phillips, W.A. 1997. Activation functions, computational goals and learning rules for local processors with contextual guidance. Neural Computation 9,763-768. Langton, C.D. 1986. Studying artificial life with cellular automata. Physica D 22, 120-149. Langton, CD. 1990. Computation at the edge of chaos: phase transitions and emergent computation. Physica D 42, 12-37. Liley, D.T.J., Wright, J.J. 1994. Intracortical connectivity of pyramidal and stellate cells: estimates of synaptic densities and coupling symmetry. Network 5, 175-189. Livingstone, M.S. 1996. Oscillatory firing and interneuronal correlations in squirrel monkey striate cortex. J. Neurophysiol. 75, 2467-2485. Lumer, E.D., Edelman, G.M., Tononi, G. 1997a. Neural dynamics in a model of the thalamocortical system. I. Layers, loops, and the emergence of fast synchronous rhythms. Cerebral Cortex 7, 207-227. Lumer, E.D., Edelman, G.M., Tononi, G. 1997b. Neural dynamics in a model of the thalamocortical system. II. The role of neural synchrony tested through perturbations of spike timing. Cerebral Cortex 7, 228-236. Miltner, W.H., Braun, C., Arnold, M,, Witte, H., Taube, E. 1999. Coherence of gamma-band EEG activity as a basis for associative learning. Nature 397, 434-436. Munk, M.H.J., Roelfsema, P.R., Konig, P., Engel, A.K., Singer, W. 1996. Role of reticular activation in the modulation of intracortical synchronisation. Science 272, 271-273. Neuenschwander S., Singer, W. 1996. Long range synchronisation of oscillatory light responses in the cat retina and lateral geniculate nucleus. Nature 379, 728-733. von Neumann, J. 1949. Theory of self-reproducing automata. In: A.W. Burkes (Ed.) University of Illinois Lectures on the Theory and Organisation of Complicated Automata. University of Illinois Press, Urbana, Il. 1966. Novikov, E., Novikov, A., Shannahof-Khalsa, D., Schwartz, B., Wright, J. 1997. Scale-similar activity in the brain. Physical Review E 56, R2387- R2389. Nunez, P.L. 1981. Electric Fields of the Brain. Oxford University Press.New York. Nunez, P.L 1995. Neocortical Dynamics and Human EEG Rhythms. Oxford University Press, New York. Olds, J., Milner, P. 1954. Positive reinforcement produced by electrical stimulation of the septal area and other regions of the rat brain. J. Comp. Physiol. Psychol. 47, 419-427. Palm, G., Wennekers, T. 1997. Synchronicity and its use in the brain. Behavioral and Brain Sciences 20, 695-696. Phillips, W.A., Singer, W. 1997. In search of common foundations for cortical computation. Behavioral and Brain Sciences 20, 657-722. Phillips, W.A., Pflieger, M.E. 1999. EEG studies of interactions that coordinate cortical activity. In: T. Nakada (ed.) Human Higher Function I: Advanced methodologies. Smith- Gordon/Nishuma. Posner, M.I., Petersen, S.E. 1990. The attention system of the human brain. Annual Review of Neuroscience 13, 25-42. Rennie, C.J., Robinson, P.A., Wright, J.J. 1999. Effects of local feedback on dispersion of electrical waves in the cerebral cortex. Physical Review E. 59, 3320-3329. Rennie, C.J., Wright, J.J., Robinson, P.A. 2000a. Mechanisms of cortical electrical activity and the emergence of gamma rhythm. J. Theoretical. Biol., (in press) Rennie, C.J., Robinson, P.A., Wright, J.J. 2000b. Mechanisms for modelling of evoked potentials in the brain. (in preparation) Robinson, P.A., Rennie, C.J., Wright, J.J. 1997. Propagation and Stability of Waves of Electrical Activity in the Cerebral Cortex. Physical Review E. 56, 826-840. Robinson, P.A., Wright, J.J., Rennie, C.J. 1998a. Synchronous Oscillations in the Cerebral Cortex. Physical Review E. 57, 4578-4588. Robinson, P.A., Rennie, C.J., Wright, J.J., Bourke, P.D. 1998b. Steady states and global dynamics of electrical activity in the cerebral cortex. Physical Review E 58, 3557- 3571. Robinson, P.A., Rennie, C.J., Wright, J.J., Gordon, E., Bahramali, H. 2000. Direct prediction of EEG spectra from physiology. (submitted) Robinson, P.A., Rennie, C.J., Wright, J.J., Gordon, E. Neurophysiological prediction of electroencephalographic spectra in sleeping and waking states. (in preparation) van Rotterdam, A., Lopes da Silva, F.H., van den Ende, J., Viergever, M.A., Hermans, A.J. 1982. A model of the spatio- temporal characteristics of the alpha rhythm. Bulletin of Mathematical Biology 44, 283-305. Singer, W. 1994. Putative functions of temporal correlations in neocortical processing. In: Koch C. and Davis JL (Eds.) Large Scale Neuronal Theories of the Brain. MIT Press, Cambridge Mass., London. Singer, W., Gray, C.M. 1995. Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 18, 555-586. Steriade, M., Gloor, P., Llinas, R.R., Lopes da Silva, F.H., Mesulam, M.M. 1990. Basic mechanisms of cerebral rhythmic activities. Electroenceph. clin. neurophysiol. 76, 481-508. Steriade, M., Amzica, F., Contreras, D. 1996. Synchronisation of fast (30-40 Hz) spontaneous cortical rhythms during brain activation. Journal of Neuroscience 16, 392-417. Stryker, M.P. 1989. Is grandmother an oscillation? Nature 388, 297-298. Thomson, A.M. 1997. Activity dependent properties of synaptic transmission at two classes of connections made by rat neocortical pyramidal neurons in vitro. J. Physiol. 502, 131- 147. Thomson, A.M., West, D.C., Hahn, J., Deuchars, J. 1996. Single axon IPSP's elicited in pyramidal cells by three classes of interneurones in slices of rat neocortex. J. Physiol. 496, 81-102. Tones, M.V., Westbrook, G.L. 1996. The impact of receptor desensitization on fast synaptic transmission. Trends in Neuroscience 19, 96-101. Traub, R.D., Whittington, M.A., Stanford, I.M., Jeffereys, J.G.R. 1996. A mechanism for generation of long range synchronous fast oscillations in the cortex. Nature 383, 621- 624. Walter, D.O., Kado, B.S., Rhodes, J.M., Adey, W.R. 1967. Electroencephalographic baselines in astronaut candidates estimated by computation and pattern recognition techniques. Aerospace Medicine 38, 371-379. Whittington, M.A., Traub, R.D., Jefferys, J.G.R. 1995. Synchronised oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature 373, 612- 615. Wilson, M.A., Bower, J.M. 1991. A computer simulation of oscillatory behaviour in primary visual cortex. Neural Computation 3, 498-509. Wilson, H.R., Cowan, J.D. 1973. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13, 55-80. Wolfram, S. 1984. Universality and complexity in cellular automata. Physica D 10, 1-35. Wright, J.J. 1990. Reticular activation and the dynamics of neuronal networks. Biol. Cybern. 62, 289-298. Wright, J.J., Liley, D.T.J. 1996. Dynamics of the brain at global and microscopic scales. Neural networks and the EEG. Behavioral and Brain Sciences 19, 285-320. Wright ,J.J. 1997a. EEG simulation: variation of spectral envelope, pulse synchrony and approx. 40Hz oscillation. Biol. Cybern. 76,181-194. Wright, J.J. 1997b. Local attractor dynamics will introduce further information to synchronous neuronal fields. Behavioural and Brain Sciences 20, 701-702. Wright, J.J. 1999. Simulation of EEG: Dynamic changes in synaptic efficacy, cerebral rhythms, and dissipative and generative activity in cortex. Biological Cybernetics 81,131- 147. Wright, J.J., Bourke, P.D., Chapman, C.L. 2000. Synchronous oscillation in the cerebral cortex and object coherence: simulation of basic electrophysiological findings. Biological Cybernetics (in press) Xu, J.H., Liu, Z.R., Liu, R., Yang, Q.F. 1997. Information transmission in human cerebral cortex. Physica D 106, 363- 374. Zhadin, M.N. 1994. Formation of rhythmic processes in the bioelectrical activity of the cerebral cortex. Biophysics 39, 133-150. Images and Figures
Figure 1 The middle panels of figure 1 show how at a larger scale, these foci of excited cortex generate waves of cortical electrical activity spreading into the less excited surrounding cortical tissue (middle left panel). The resulting wave activity can be analysed by cross-correlation, as shown in the middle right panel. Here the lag time for maximally correlated activity (with reference to the recording site shown in the left middle panel) is displayed for the extended field. It is seen that the foci of activity have entered "synchronous oscillation". The lower panels in figure 1 show the overall brain, and EEG activity as generated in simulations - from low frequency "theta" activity, through the alpha, beta and gamma ranges, to 40Hz. These progressive changes in frequency content reflect the overall level of cortical excitation. At the highest levels of excitation, the self-excited cortical state described in the top panels has been reached. 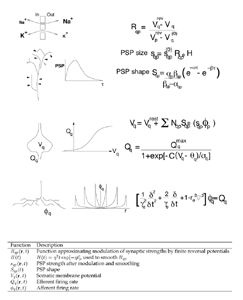
Figure 2 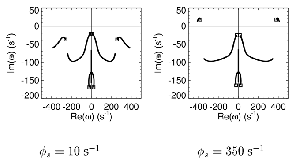
Figure 3 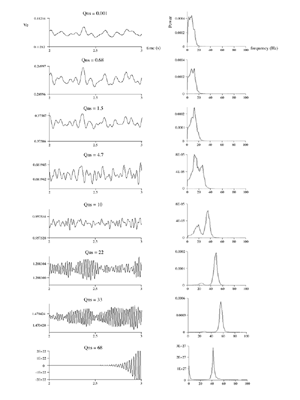
Figure 4 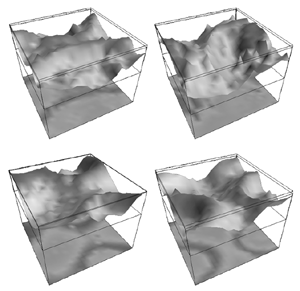
Figure 5 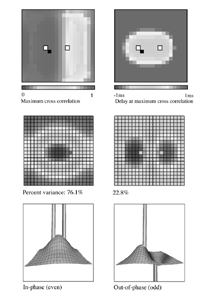
Figure 6 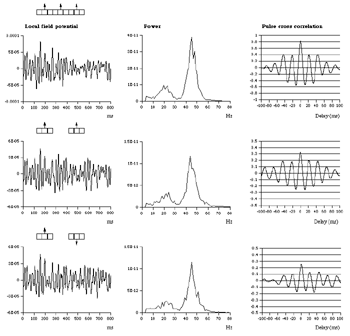
Figure 7 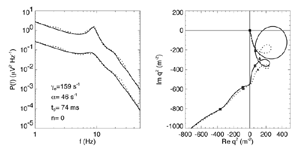
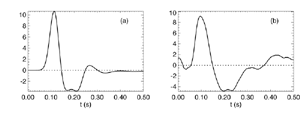
Figure 8 Fits were achieved by varying only the fraction of thalamocortical feedback and the general level of cortical gain, including cortical activation. Right hand figure: Complex loci of the wavenumber-independent part of the spectral content attributable to the thalamo- cortical resonance alone. Solid line eyes closed - dashed, eyes open Figure 9Simulation of the ERP based upon impulse response of the thalamocortical resonance model.
Figure 9a 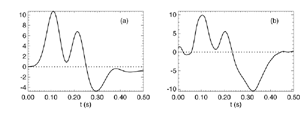
Figure 9b 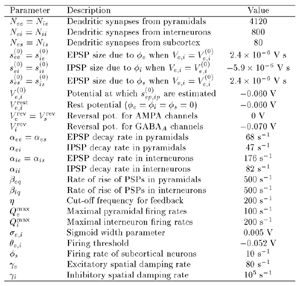
Table 1 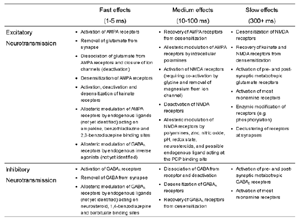
Table 2 |