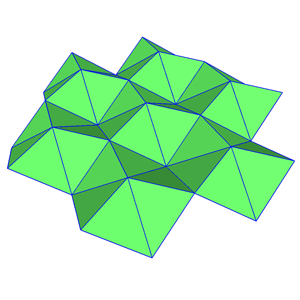
Plexagon - Pleated Hexagon
(hexagonal dipyramidal scanelohedra)
Written by Paul Bourke
Based upon concepts/work by Ron Evans
February 2000
Quote
|
A new modular building geometry--Plexagon is a new modular geometry
based on the radial pleating of polygonal plates, and their joining or
co-bracing into 3D modules. This engineering approach can form a very
practical basis for modular greenhouses (using recycled plastic sheeting)
and modular homes (using fibrous and metal sheeting) for the world's
homeless and refugees. The word Plexagon is an abbreviation of
"pleated hexagon". Plexagon is a newly-identified family of
hexagonal dipyramidal scanelohedra.
Ron Evans
|
Construction
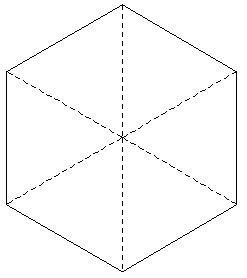
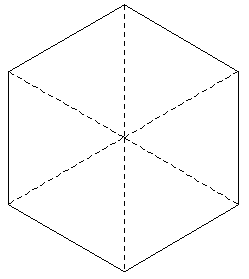
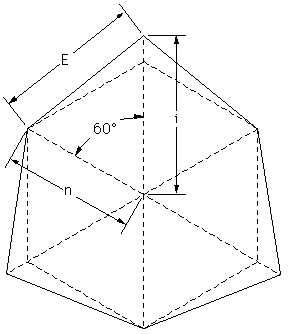
The construction of a plexagon is illustrated below. Start with two
hexagons with radius and edge length "n", extend every second radial
length to "i", fold the radial edges in the appropriate direction,
and finally join the two halves together.
| |
"Bottom" face |
"Top" face |
Hexagon
(2D) |
 |
 |
Extend
alternate
vertices
(2D) |
 |
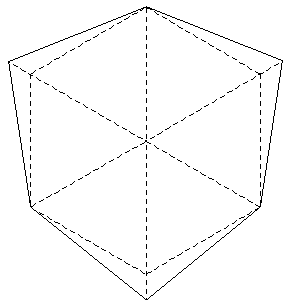 |
| |
E2 = n2 - n i + i2 |
|
Fold
edges
above
or
below
plane
(2D) |
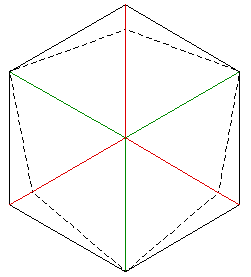 |
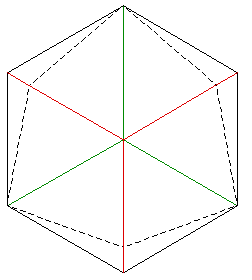 |
Join
"top"
and
"bottom"
sheets
(3D view) |
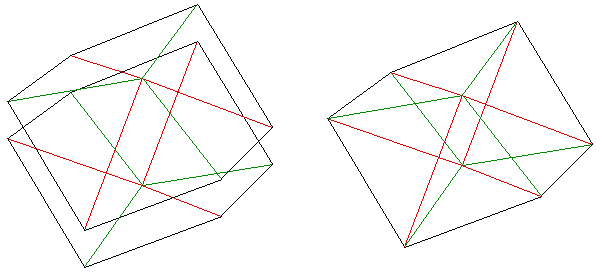 |
Animation illustrating plexagon formation
Templates for making your own plexagon
The instructions above make it easy to measure and cut the top and bottom
plexagon pieces from stiff paper. To make it easier for two specific
plexagons the following two files can be printed, they represent the
T90 and T120 plexagons.
You should be able to print these directly from your browser, they will
fit onto both A4 and US-Letter paper sizes.
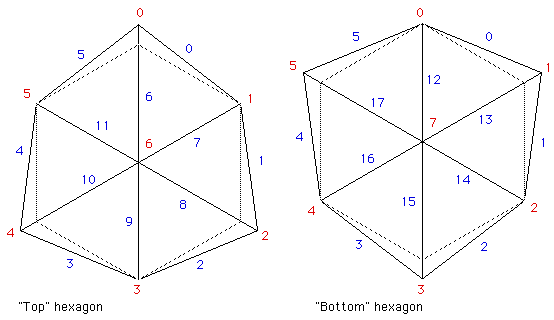
Vertex and edge numbering conventions
Numbering conventions for vertices and edges in the computer model.
|
Two plexagon panels can be joined by taking the "sawtooth" edge
of one, reversing it, and joining it at some angle to the "sawtooth"
edge of another panel. The angle (T) the panels need to be rotated by
in order to form a perfect seal depends upon the ratio of "i" and "n".
This is illustrated on the right.
As the ratio i/n (pleat ratio)
is increased the rotation angle T decreases. T is
at a maximum (180) as i approaches n (a flat sheet). As i/n increases
the plexagon panels will eventually intersect each other at about i/n
equal to 1.31.
Animation illustrating T angle
|
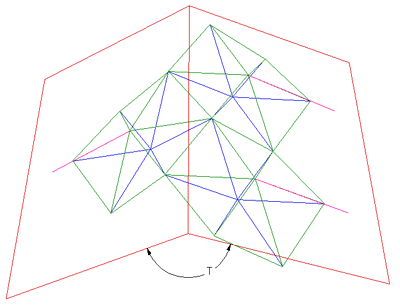 |
Table of n, i, E, and T (degrees)
n i E T
======== ======== ======== ==========
1.000000 1.866760 Golden ratio dxf, pov, vision3d, OBJ
1.000000 1.700000 1.479865 46.233918
1.000000 1.690000 1.471768 46.659752
1.000000 1.680000 1.463694 47.093682
1.000000 1.670000 1.455644 47.535952
1.000000 1.660000 1.447619 47.986815
1.000000 1.650000 1.439618 48.446535
1.000000 1.640000 1.431642 48.915387
1.000000 1.630000 1.423692 49.393660
1.000000 1.620000 1.415768 49.881654
1.000000 1.610000 1.407871 50.379684
1.000000 1.600000 1.400000 50.888078 dxf, pov, vision3d, OBJ
1.000000 1.590000 1.392157 51.407180
1.000000 1.580000 1.384341 51.937350
1.000000 1.570000 1.376554 52.478966
1.000000 1.560000 1.368795 53.032424
1.000000 1.550000 1.361066 53.598140
1.000000 1.540000 1.353366 54.176549
1.000000 1.530000 1.345697 54.768111
1.000000 1.520000 1.338058 55.373307
1.000000 1.510000 1.330451 55.992646
1.000000 1.500000 1.322876 56.626663
1.000000 1.490000 1.315333 57.275922
1.000000 1.480000 1.307823 57.941019
1.000000 1.470000 1.300346 58.622583
1.000000 1.460000 1.292904 59.321280
1.000000 1.450520 1.285880 60.000000 dxf, pov, vision3d, OBJ
1.000000 1.450000 1.285496 60.037814
1.000000 1.440000 1.278124 60.772933
1.000000 1.430000 1.270787 61.527428
1.000000 1.420000 1.263487 62.302141
1.000000 1.410000 1.256225 63.097968
1.000000 1.400000 1.249000 63.915861
1.000000 1.390000 1.241813 64.756839
1.000000 1.380000 1.234666 65.621985
1.000000 1.370000 1.227559 66.512462
1.000000 1.360000 1.220492 67.429513
1.000000 1.350000 1.213466 68.374472
1.000000 1.340000 1.206482 69.348774
1.000000 1.330000 1.199542 70.353962
1.000000 1.320000 1.192644 71.391702
1.000000 1.310000 1.185791 72.463794
1.000000 1.300000 1.178983 73.572190
1.000000 1.290000 1.172220 74.719007
1.000000 1.280000 1.165504 75.906551
1.000000 1.270000 1.158836 77.137338
1.000000 1.260000 1.152215 78.414123
1.000000 1.250000 1.145644 79.739929
1.000000 1.240000 1.139122 81.118086
1.000000 1.230000 1.132652 82.552277
1.000000 1.220000 1.126233 84.046586
1.000000 1.210000 1.119866 85.605564
1.000000 1.200000 1.113553 87.234305
1.000000 1.190000 1.107294 88.938542
1.000000 1.184000 1.103565 90.000000 dxf, pov, vision3d, OBJ
1.000000 1.180000 1.101090 90.724759
1.000000 1.170000 1.094943 92.600334
1.000000 1.160000 1.088853 94.573726
1.000000 1.150000 1.082820 96.654702
1.000000 1.140000 1.076847 98.854642
1.000000 1.130000 1.070934 101.186934
1.000000 1.120000 1.065082 103.667510
1.000000 1.110000 1.059292 106.315585
1.000000 1.100000 1.053565 109.154694
1.000000 1.090000 1.047903 112.214204
1.000000 1.080000 1.042305 115.531598
1.000000 1.070000 1.036774 119.156064
1.000000 1.067800 1.035567 120.000000 dxf, pov, vision3d, OBJ
1.000000 1.060000 1.031310 123.154476
1.000000 1.050000 1.025914 127.622055
1.000000 1.040000 1.020588 132.703231
1.000000 1.035924 1.018437 135.000000 dxf, pov, vision3d, OBJ
1.000000 1.030000 1.015332 138.638092
1.000000 1.020000 1.010149 145.888603
1.000000 1.010000 1.005037 155.630794
|
|
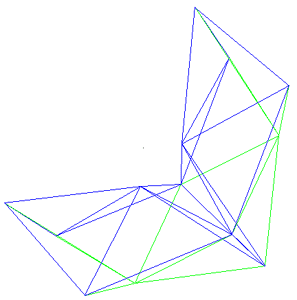
The turning angle T defined in this way is the same as the interior
angle if two plexagons are joined as shown in the diagram on the right.
That is, joining two plexagons such that they share two "E" length edges,
(there is only one way to do this).
|
|
Radius (R)
|
The plexagon radius R is the maximum radius of the plexagon if it is
projected onto its radial plane. Note that this is not simply the length
of the longest hexagonal rib because the ribs are angled in the dimension
perpendicular to the radial plane.
The value of R given a plexagon "i"
and "n" can be found by solving the following:
E2 = R2 + [
sqrt(i2 - R2) - sqrt(n2 - R2)
]2
E was given earlier in terms of i and n as
E2 = n2 - n i + i2
|
|
Photographic contribution by Gayla Chandler
|