Gaussian EliminationSolving simultaneous equationsWritten by Paul BourkeAugust 1997
The following note will briefly discuss the standard method of solving simultaneous equations. It will also present C source which implements the so called "partial pivoting" algorithm. An example of 3 simultaneous equations with 3 unknowns x0, x1, x2 is shown below
We wish to determine the values of the 3 unknowns. The solution basically relies on us being able to multiply a row by a constant, and add (or subtract) two rows. So for example the first row above could be multiplied by -2 and then the second row could be added to it to give a new set of equations (but with the same solution)
The rows and factor chosen was designed to eliminate the first unknown x0 from the second equation. If we now take -1 times the first row and add the last row we get
And finally, adding the last two rows gives
The above is known as the elimination phase, the aim is to turn all the elements below the diagonal into zeros. The solution can now be determined by so called "back substitution". From the last equation we see that x2 is -16. Substituting this value into the second equation gives x1 = 15, and finally substituting these two values into the first equation gives the last unknown x0 = 1. In general a series of simultaneous equations can be written in matrix notation. If we have n equations with n unknowns (x0, x1, x2, ... xn-1) this can be written as 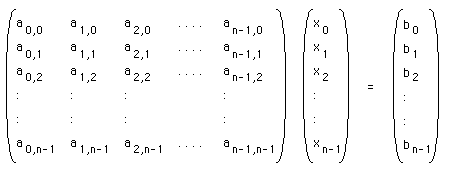
This is often written in a more compact way as A x = b, where
A is a matrix, x and b are vectors.
The Gaussian elimination process consists of two steps, first reducing
the elements below the diagonal to 0 and second, back substituting
to find the solutions.
In order to eliminate the appropriate element it is not sufficient to
simply use a ratio based automatically on the values on the elements
column as this may result in a divide by zero. The usual
solution is to swap the rows around so that the element being removed
has the largest magnitude. The following source code implements the above algorithm in a straightforward way, there are improvements that could be made especially for sparse systems of equations (a large number of equations with mostly zero elements). C source example
/*
Solve a system of n equations in n unknowns using Gaussian Elimination
Solve an equation in matrix form Ax = b
The 2D array a is the matrix A with an additional column b.
This is often written (A:b)
A0,0 A1,0 A2,0 .... An-1,0 b0
A0,1 A1,1 A2,1 .... An-1,1 b1
A0,2 A1,2 A2,2 .... An-1,2 b2
: : : : :
: : : : :
A0,n-1 A1,n-1 A2,n-1 .... An-1,n-1 bn-1
The result is returned in x, otherwise the function returns FALSE
if the system of equations is singular.
*/
int GSolve(double **a,int n,double *x)
{
int i,j,k,maxrow;
double tmp;
for (i=0;i<n;i++) {
/* Find the row with the largest first value */
maxrow = i;
for (j=i+1;j<n;j++) {
if (ABS(a[i][j]) > ABS(a[i][maxrow]))
maxrow = j;
}
/* Swap the maxrow and ith row */
for (k=i;k<n+1;k++) {
tmp = a[k][i];
a[k][i] = a[k][maxrow];
a[k][maxrow] = tmp;
}
/* Singular matrix? */
if (ABS(a[i][i]) < EPS)
return(FALSE);
/* Eliminate the ith element of the jth row */
for (j=i+1;j<n;j++) {
for (k=n;k>=i;k--) {
a[k][j] -= a[k][i] * a[i][j] / a[i][i];
}
}
}
/* Do the back substitution */
for (j=n-1;j>=0;j--) {
tmp = 0;
for (k=j+1;k<n;k++)
tmp += a[k][j] * x[k];
x[j] = (a[n][j] - tmp) / a[j][j];
}
return(TRUE);
}
A simple calling program which solves the example earlier is
#define ABS(x) (x < 0 ? -(x) : (x))
#define EPS 0.00001
#define TRUE 1
#define FALSE 0
int main(int argc,char **argv)
{
int i,n = 3;
double x[3] = {0.0,0.0,0.0};
double **a;
a = (double **)malloc((n+1)*sizeof(double *));
for (i=0;i<n+1;i++)
a[i] = (double *)malloc(n*sizeof(double));
a[0][0] = 1; a[1][0] = 1; a[2][0] = 1; a[3][0] = 0;
a[0][1] = 2; a[1][1] = 1; a[2][1] = 1; a[3][1] = 1;
a[0][2] = 1; a[1][2] = 2; a[2][2] = 1; a[3][2] = 15;
GSolve(a,n,x);
WriteSolution(a,n,x);
}
void WriteSolution(double **a,int n,double *x)
{
int j,k;
for (j=0;j<n;j++) {
for (k=0;k<n+1;k++) {
printf("%10.3f ",a[k][j]);
}
printf(" | %10.3f\n",x[j]);
}
printf("\n");
}
|