Histogram Matching

Histogram matching is a process where a time series, image, or higher dimension scalar data is modified such that its histogram matches that of another (reference) dataset. A common application of this is to match the images from two sensors with slightly different responses, or from a sensor whose response changes over time.

Histogram of reference time series	Histogram of time series to be adjusted
The example given here is a synthetically generated time series. The reference series is just a uniform random distribution, the second series is a Gaussian random distribution.	Histogram of the adjusted time series

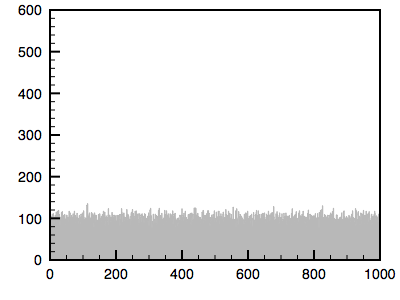
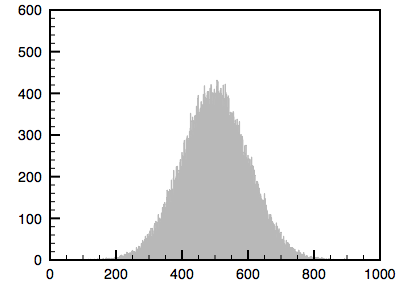
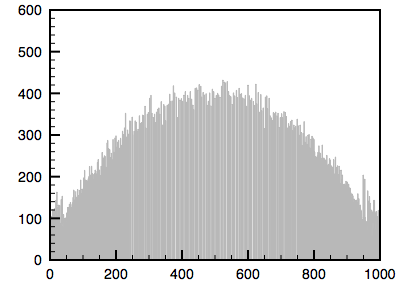
The algorithm is as follows. The cumulative histogram is computed for each dataset, see the diagram below. For any particular value (x_i) in the data to be adjusted has a cumulative histogram value given by G(x_i). This in turn is the cumulative distribution value in the reference dataset, namely H(x_j). The input data value x_i is replaced by x_j.

In practice for discrete valued data one does not step through data values but rather creates a mapping to the output state for each possible input state. In the case of an image this would be a mapping for each of the 256 different states.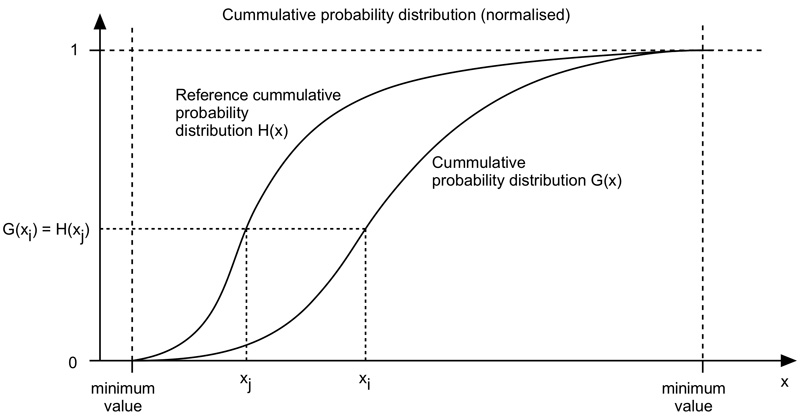

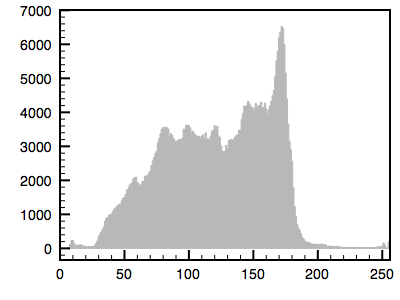
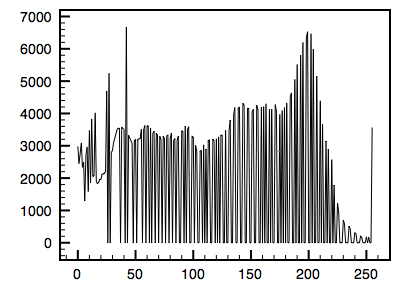
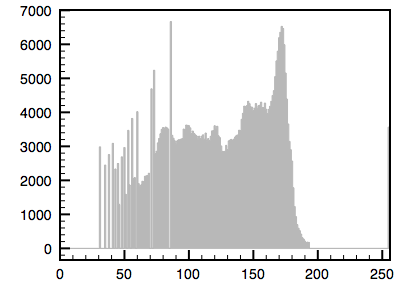
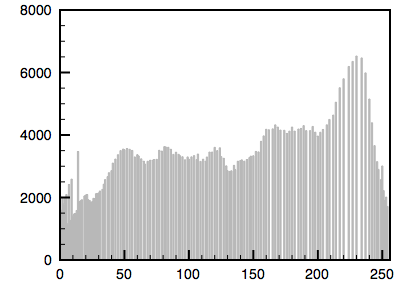
The following is an example using a greyscale image. The first image is the reference image and the histogram is given. The second image is the one whose histogram will be matched to the first. The third shows the resulting matched image.

Reference image	Histogram of reference image
Image to be adjusted	Histogram of image to be adjusted
Histogram matched image	Histogram of matched image

Notes

• In the discussion here the two datasets are assumed to have the same range of values. The size of the two datasets do not need to be the same.

• As can be seen in the examples above, the matching introduces gaps in the histograms. This is to be expected since the histograms are being distorted. This is especially so for discrete datasets such as images, it can often be reduced for continuous data by creating finer histogram bins.

• For RGB images the histogram matching can be applied in one of two ways: it can be applied to each colour channel independently or a single mapping applied to all channels. In the later case this single mapping can be derived from a greyscale version of the image, the intensity, luminance, or other similar single measures. In the case where the matching is applied on a per channel basis, colouration effects can occur particularly if one or more channels has a narrow distribution.

• histmatch.sh by Fred Weinhaus matches one image to another and is based upon functions installed with Imagemagik.

Histogram normalisation (called "equalisation" in PhotoShop) is a similar process where the reference histogram is a uniform distribution (the cumulative distribution is a constant slope). The effect is to spread the data values over the available dynamic range.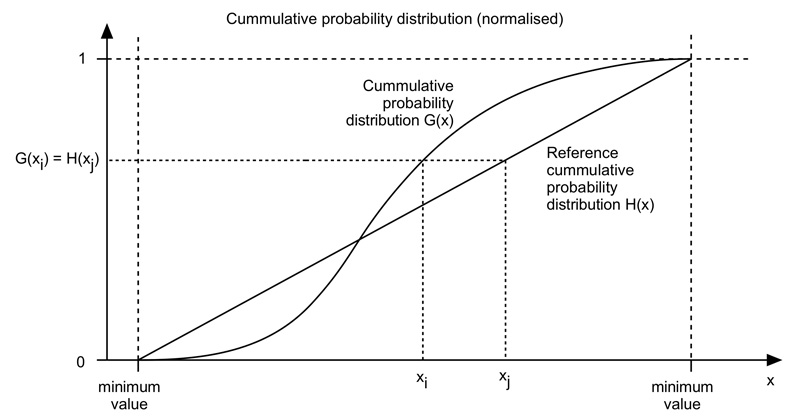

The figure illustrating the process is given above, it is the same as the earlier diagram except the reference cumulative probability distribution is a straight line rather than defined by a reference image. An example using the reference image used earlier is given below.

Normalised version of reference image above

Histogram of normalised image