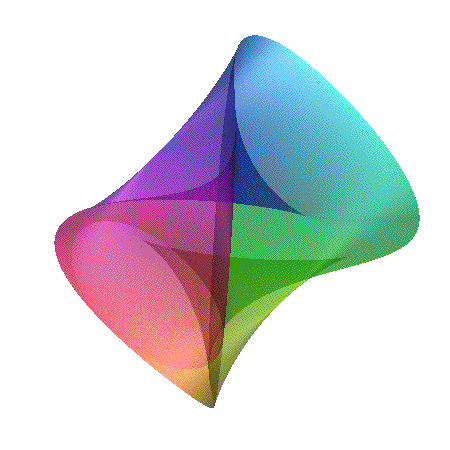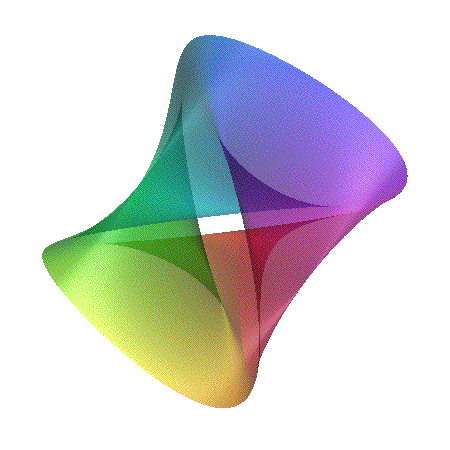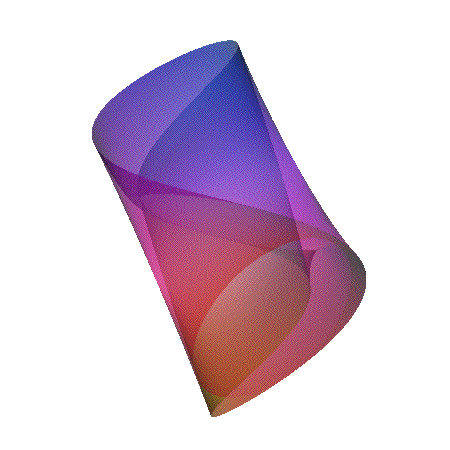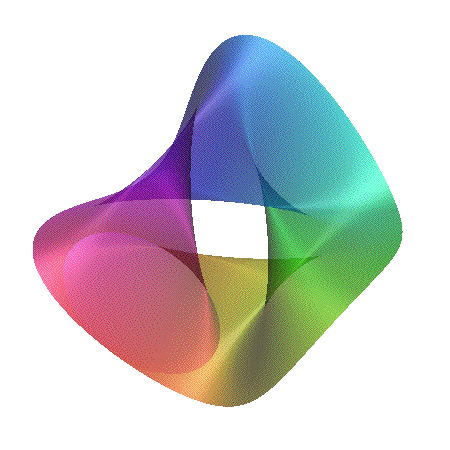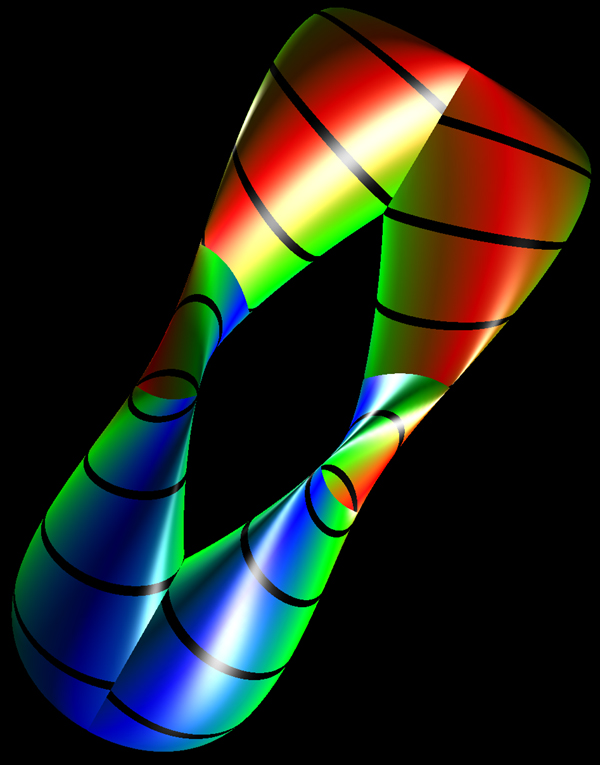The Torus and Super-torusWritten by Paul BourkeMay 1990
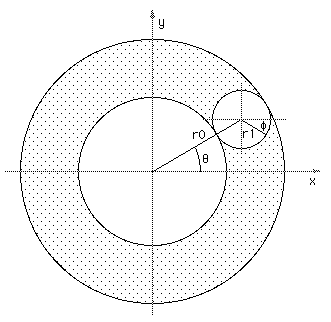
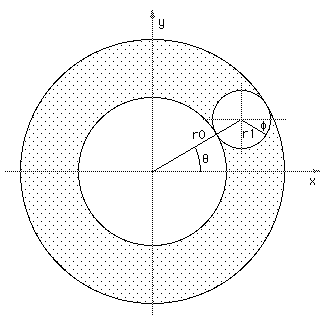
The torus is perhaps the least used object in real modelling applications but it still appears as a standard form in modelling and rendering packages ahead of far more useful geometric primitives. In any case, given the conventions below, that is, defining the radius (r0) from the center to the middle of the ring of the torus and the radius (r1) of the cross section of ring of the torus.
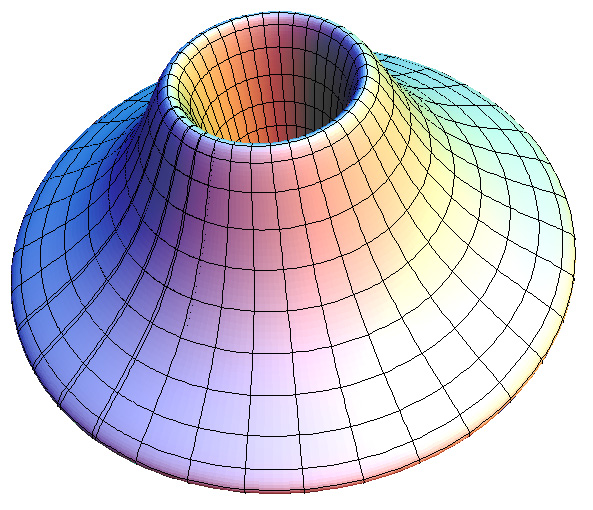
where theta and phi range from 0 to 2π. Using the above formulation a torus with center radius r0 = 1 and outer radius r1 = 0.25 will look something like this 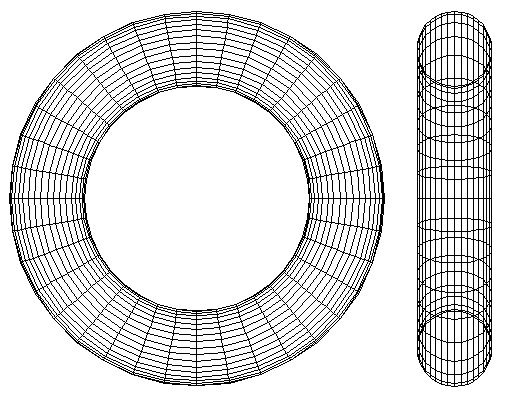 
The code for generating a facet approximation to a torus as described later involves creating facets with vertices defined by
If a facet approximation to a torus is required then a large number of facets are generally necessary to produce a smooth rendered surface. In the wire frame example above dphi and dtheta were 10 degrees, this results in 36x36=1296 facets. Another approach is to create a torus from a number of spheres which rendering packages often support more efficiently. This is achieved by simply packing spheres around a circular path, radius r0. The radius of the sphere being the radius r1. For example, the following shows the same torus dimension as in the earlier example created with 50 and 100 spheres.
C Source
This C code generated the facet representation shown above, the planar facets are exported in DXF for this example. Super-toroid - A Geometric Primitive for Computer Aided Design
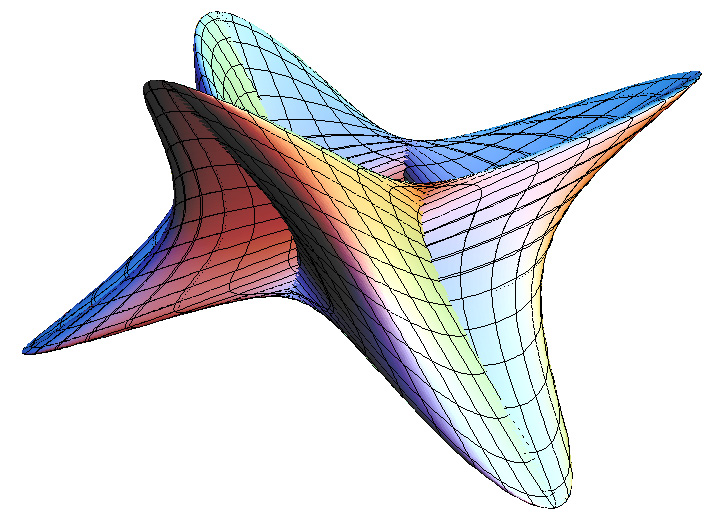
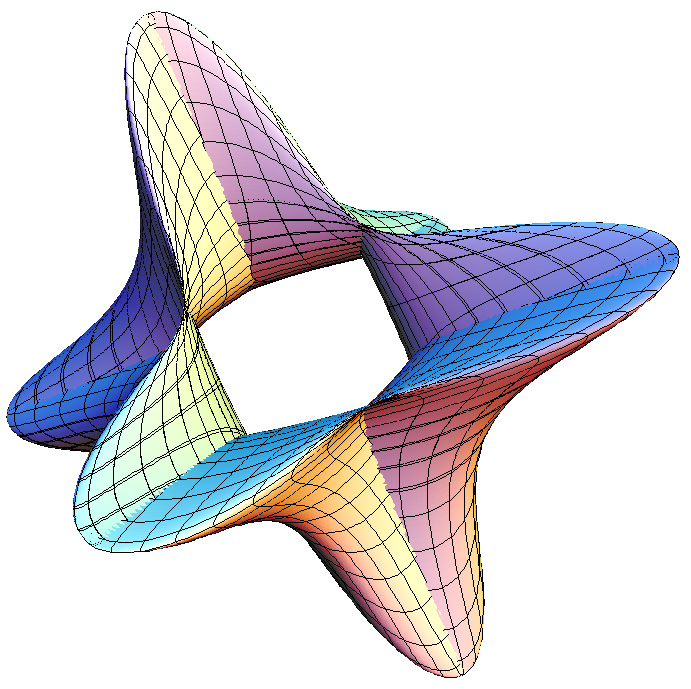
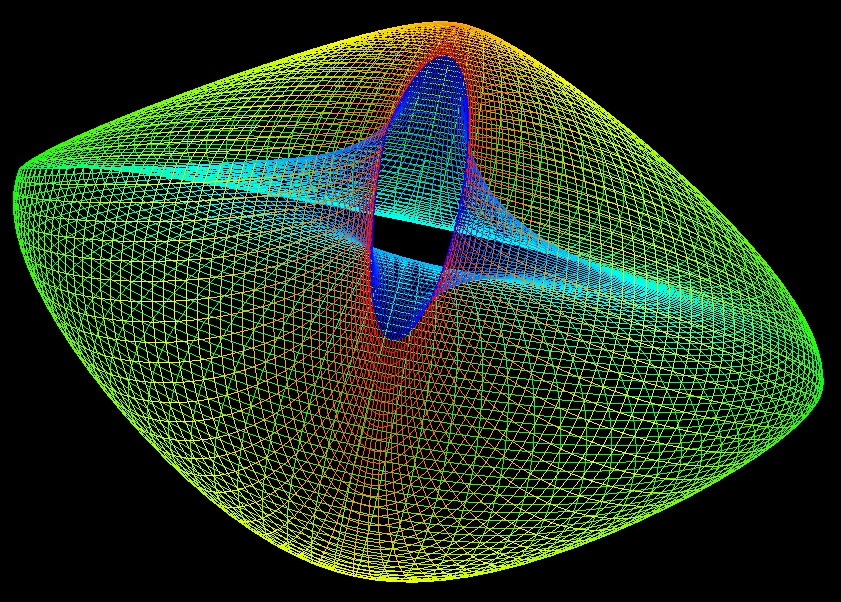
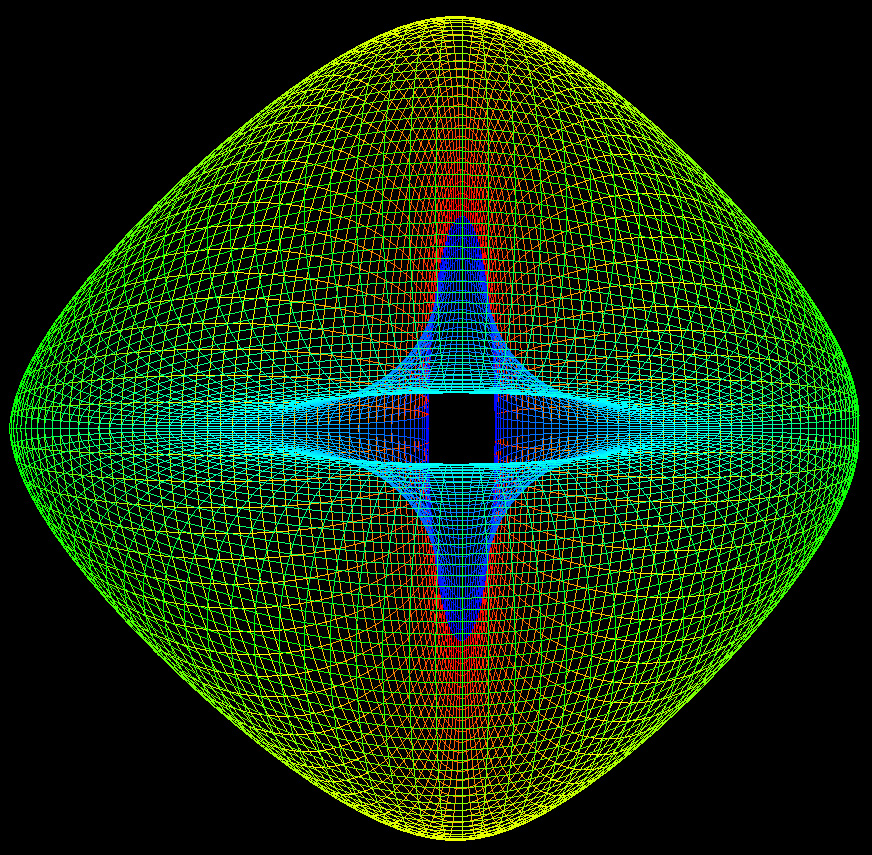
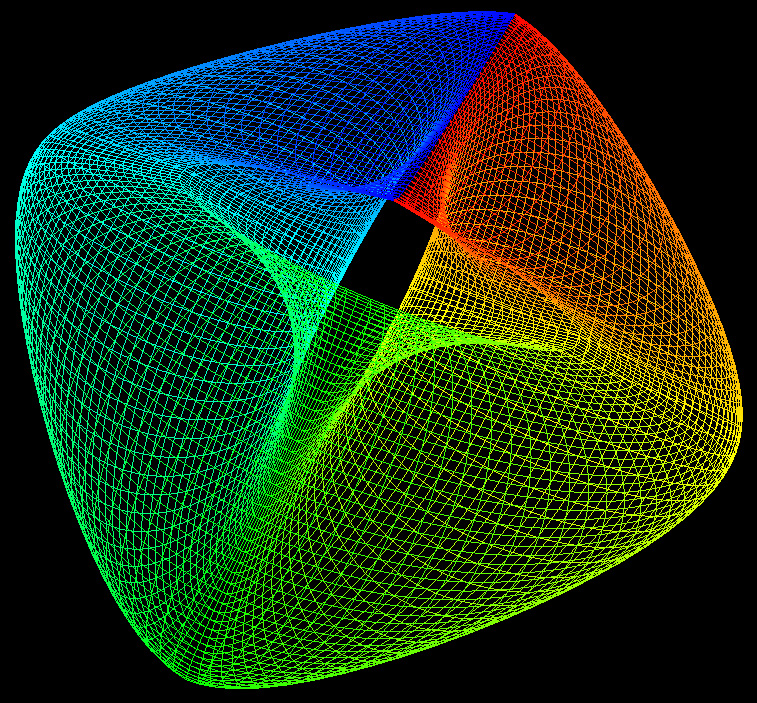
It is different values of these powers which give rise to a family of 3D shapes all basically toroidal in shape. The value of n1 determines the shape of the torus ring, n2 determines the shape of the cross section of the ring. Note that with the normal definition of power the above equations are only defined for a single quadrant, namely that where the cosine and sine terms are positive. When creating the super-torus in practice one has two choices, either replicate the result in the one quadrant to the other three with the correct mirror operations, or define xn = sign(x) * abs(x)n. Examples of the super-toroid generated for different values of n1 and n2 are shown below, of course, the legal values of n1 and n2 form a continuum of values from 0 to infinity (although there are representation issues near 0 and above 4). 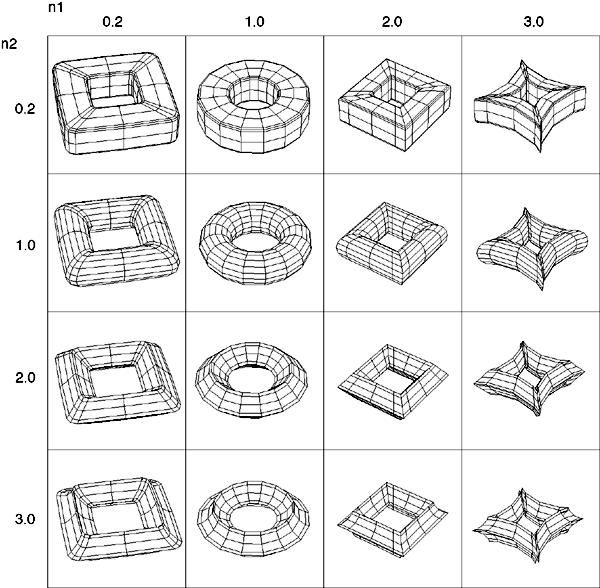
An idea of the continuum of cross sectional shapes offered by squaring the sin() and cosine() terms consider the following 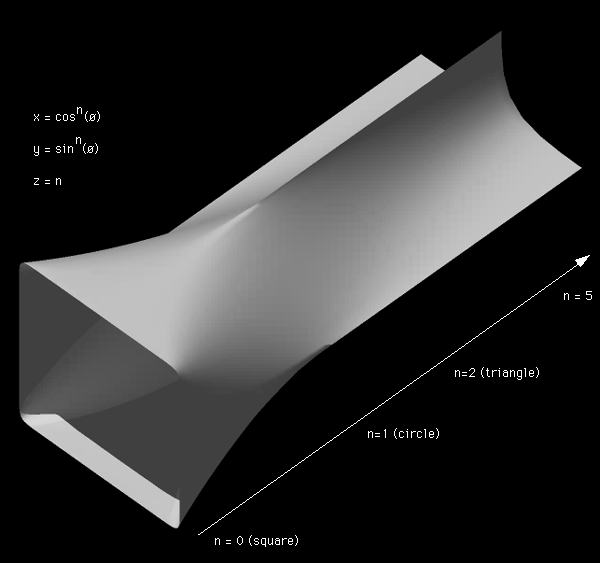 C source
Code which generates a facet based super-toroid in DXF format is given here. (Written for clarity not efficiency). Something similar for stl is here. 
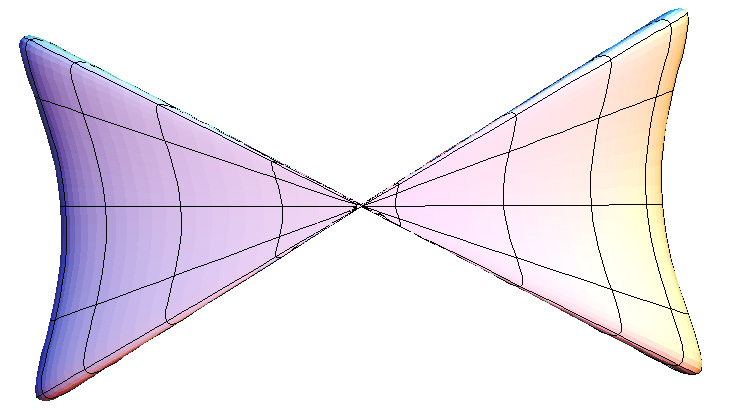
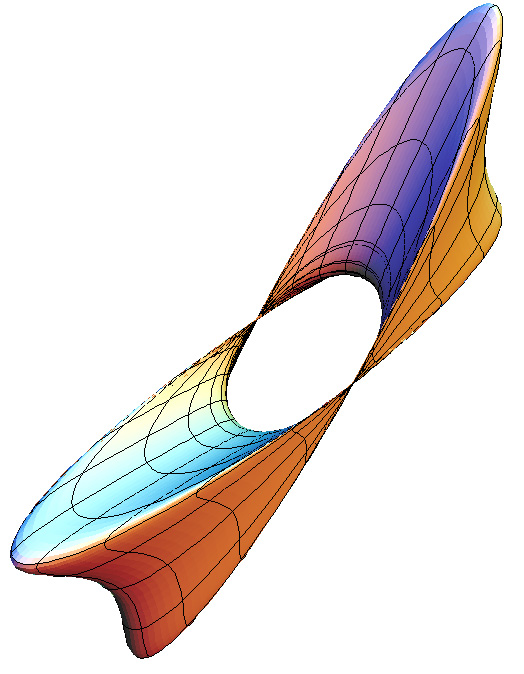
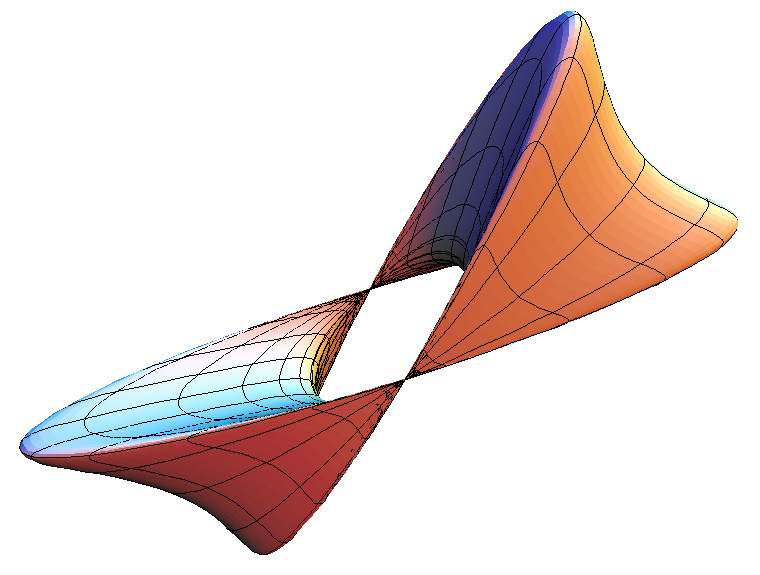
The surface doesn't intersect itself for c > 1. c = 0.5
c = 1.0
c = 1.5
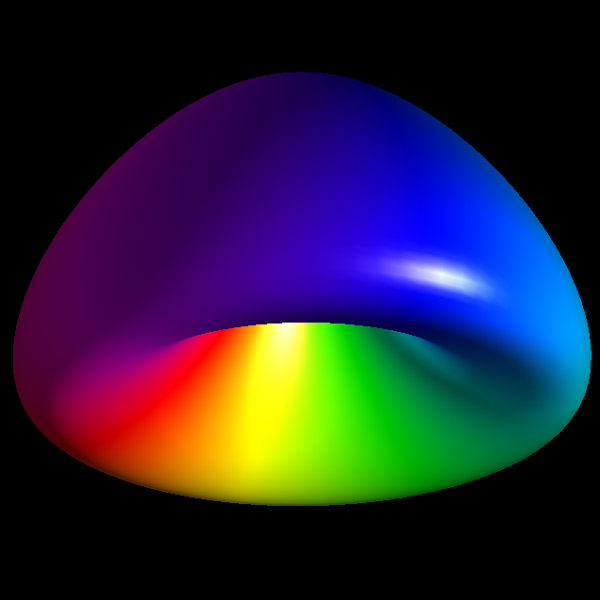
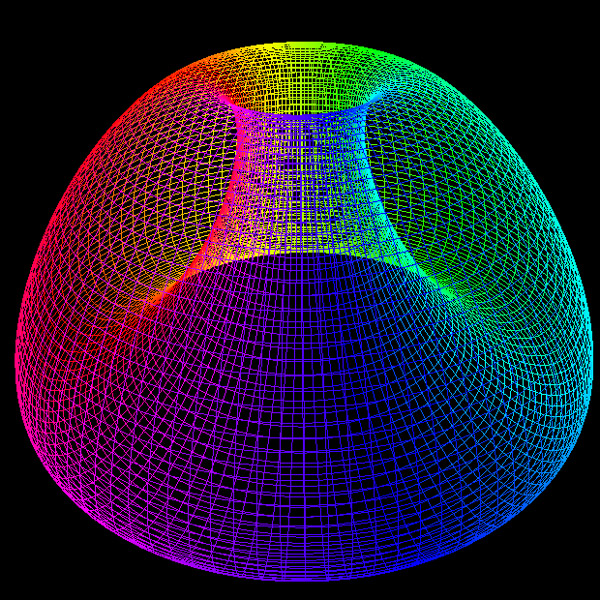

c = 2.5

Solid 
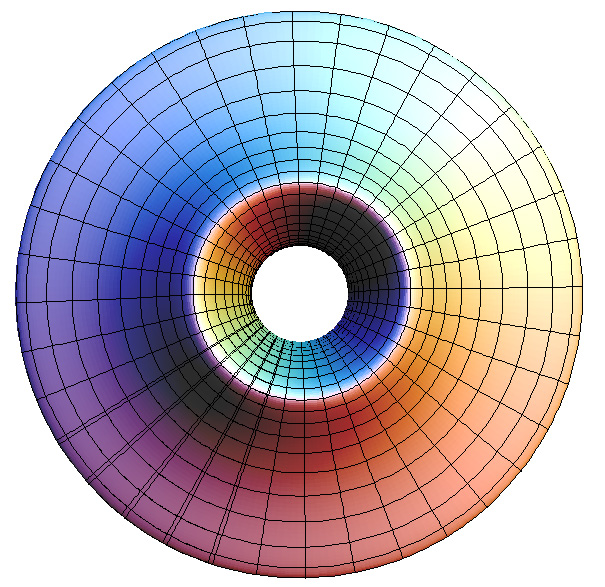
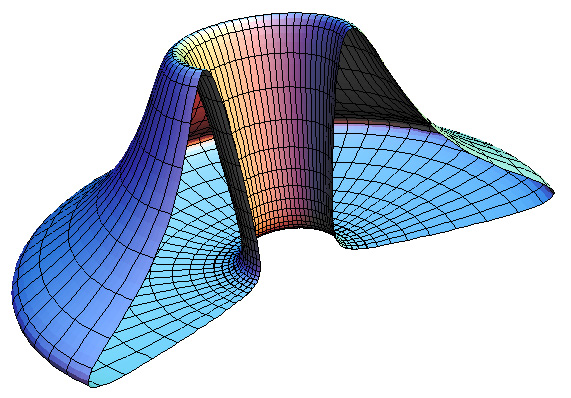
Gumdrop torusGraphics by Paul BourkeMarch 2003
PovRay scene: gumdrop.pov



c = 1


c = 1.5


c = 0.5




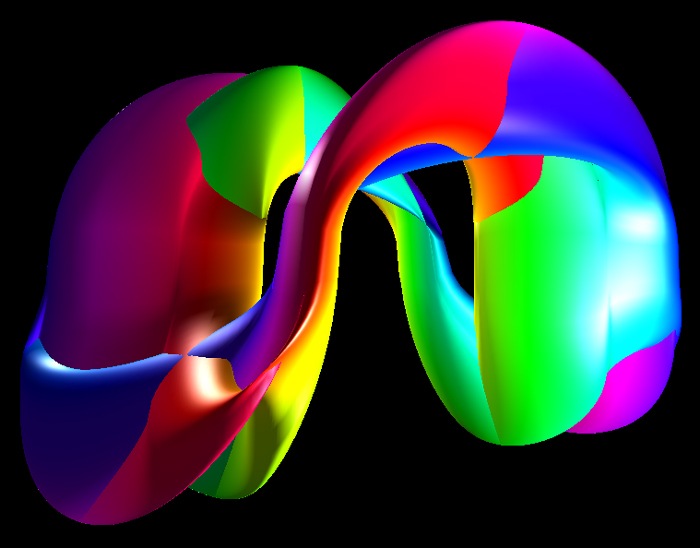


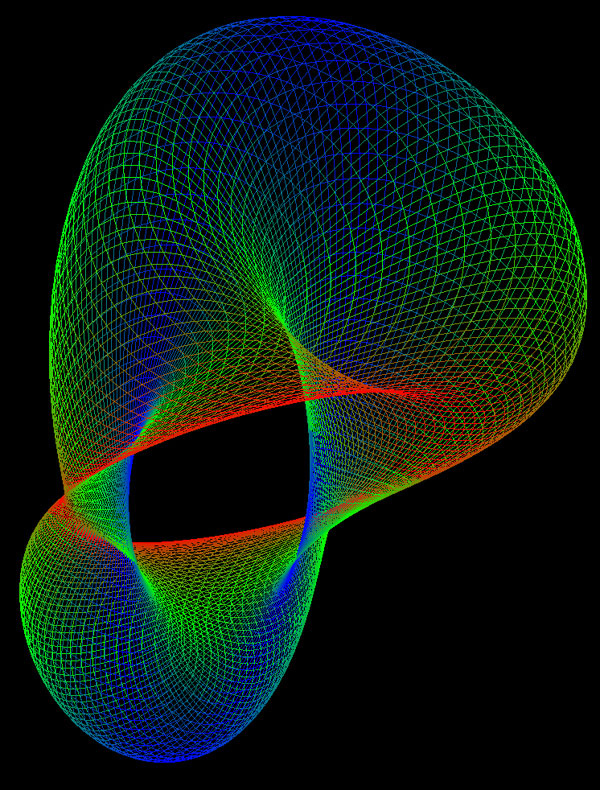
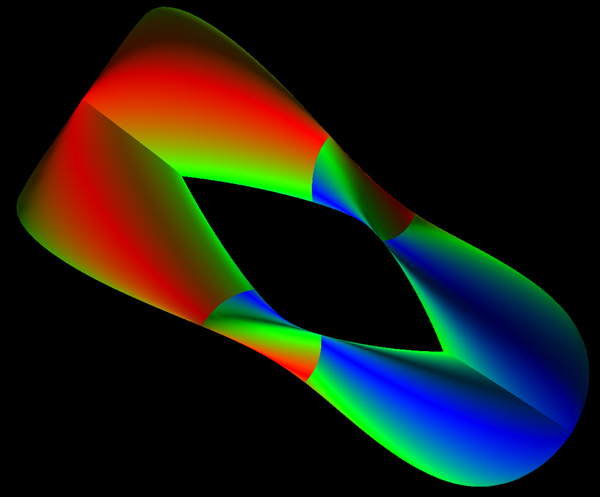
A German topologist named Klein
Most containers have an inside and an outside,
a Klein bottle is a closed surface with no interior
and only one surface. It is unrealisable in 3 dimensions
without intersecting surfaces. It can be realised in 4
dimensions. The classical representation is shown below.
The parametric equations to produce the above are:
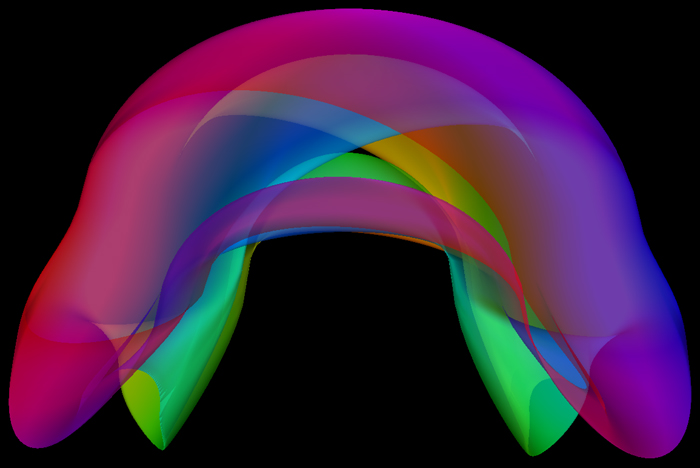
A Klein bottle can be formed by taking two Möbius strips
and join them along their boundaries, this so called
"Figure-8 Klein Bottle" can be parameterized as follows:
Source code
This source code creates geometry files
in the "geom" format. For a description of this file format see the
specifications in the 3D file formats
section. You may choose to translate the resulting geom file into your
favourite file format or modify the code to create the format of your
choice, all you need to do is modify the bit where the polygon is
written to a file. This source code creates
the classical Klein bottle shape as described at the top of this
document.
If you are used to using GeomView then
this code creates a CMESH
that can be opened directly in that package. Alternatively if you have
a package that allows plotting of regular meshes then this is the code
to grab and modify.
If you would like to create a Klein bottle for a CAD package, this
source code creates a DXF file of the classical
Klein bottle. Alternatively, here is a sample DXF file
created using the above program and tessellating the bottle by a 50x50 mesh.
September 2012
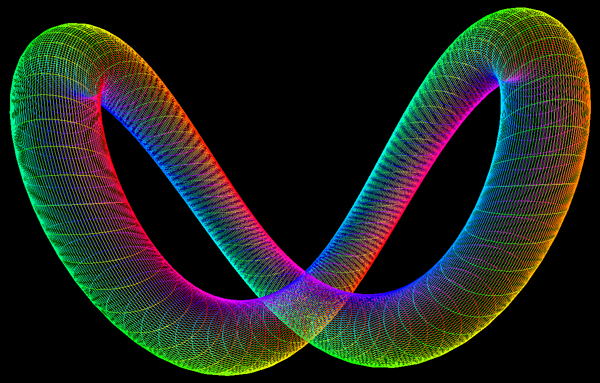
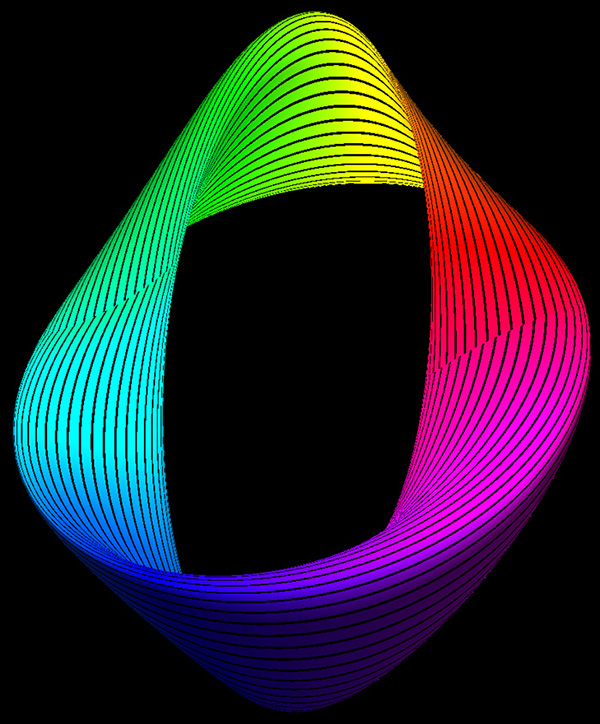
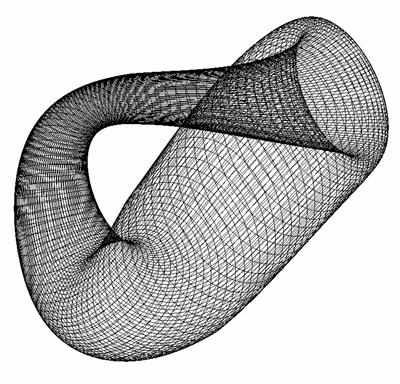
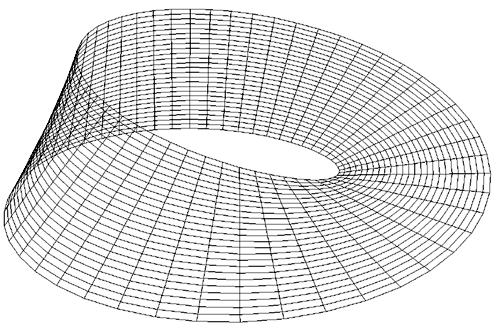
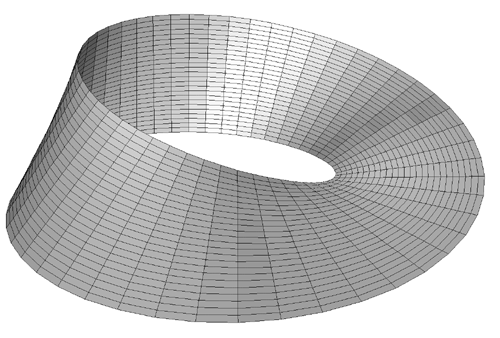
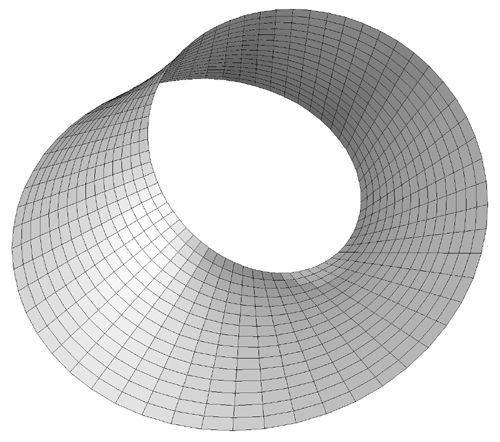
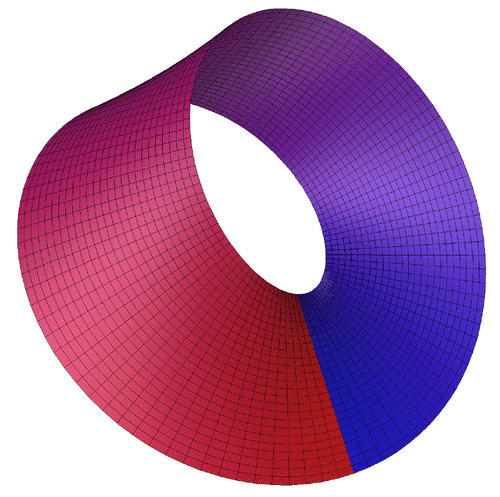
The Möbius strip is the simplest geometric shape which has only one surface
and only one edge. It can be created by taking a strip of paper, giving it a half
twist along its long axis, and then joining the two narrow ends together.
The Möbius strip in 3 dimensions can be represented parametrically f(s,t)
as follows
where s ranges from 0 to 2*π and t ranges typically from -0.4 to 0.4
An example of such a strip is shown below.
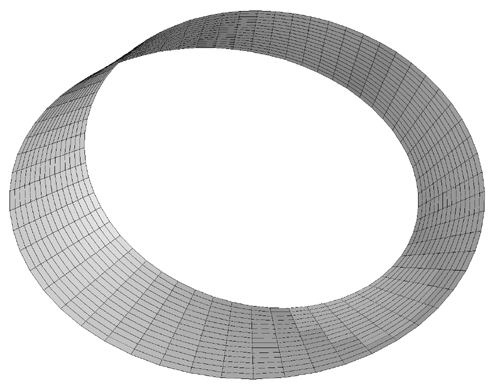
The band for different values of t are illustrated below.
t = -1 -> 1
t = -0.1 -> 0.1
t = -0.5 -> 0.5
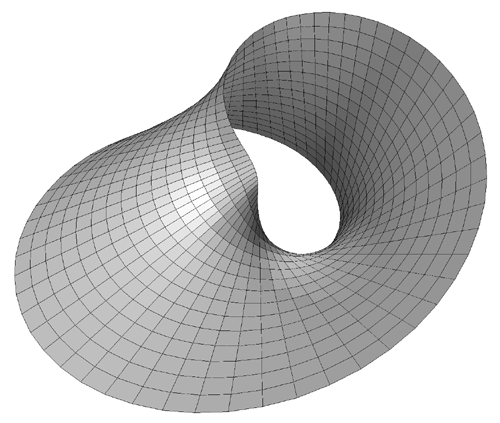
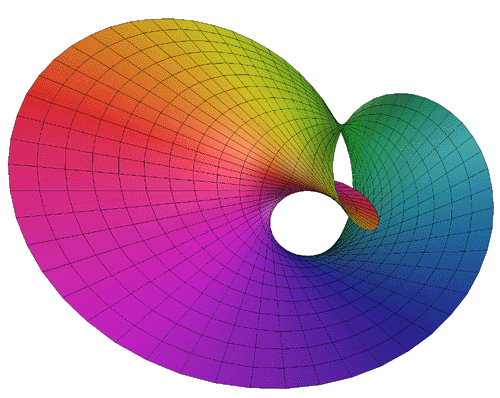
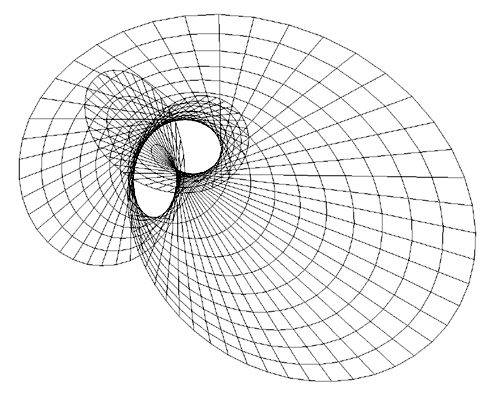
Increasing the range of t even further yields interesting folded
and increasingly convoluted forms.
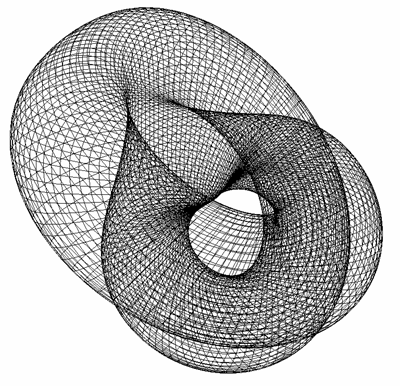
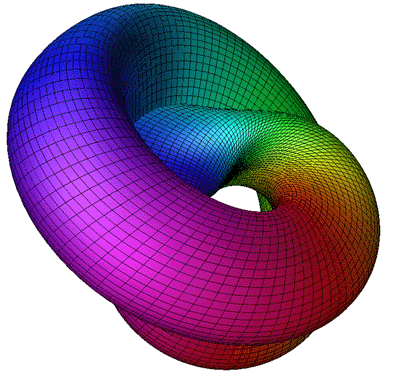
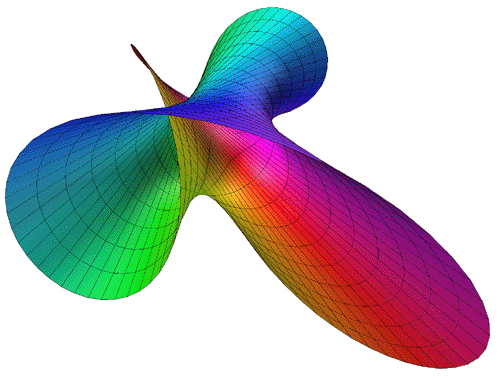
Attributed to Roger Bagula
Graphics by Paul Bourke
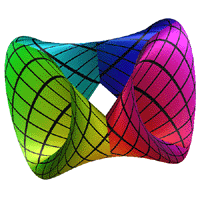
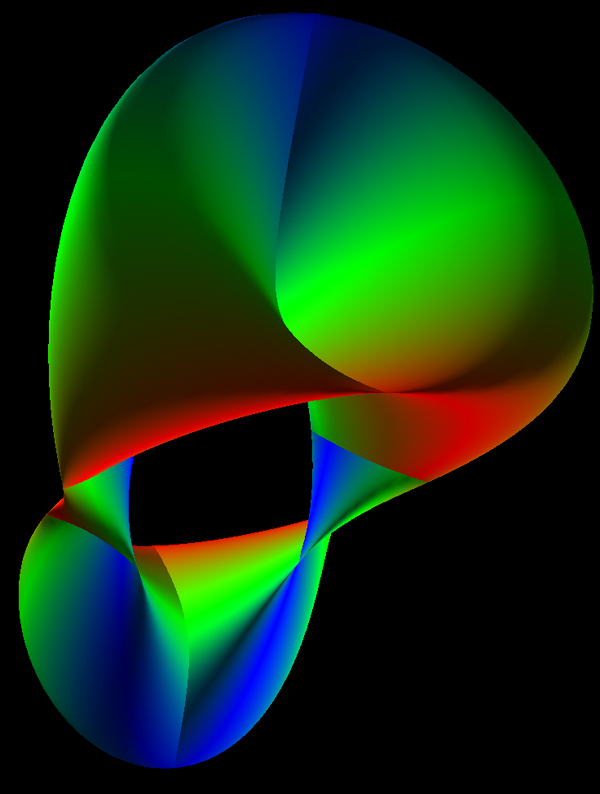
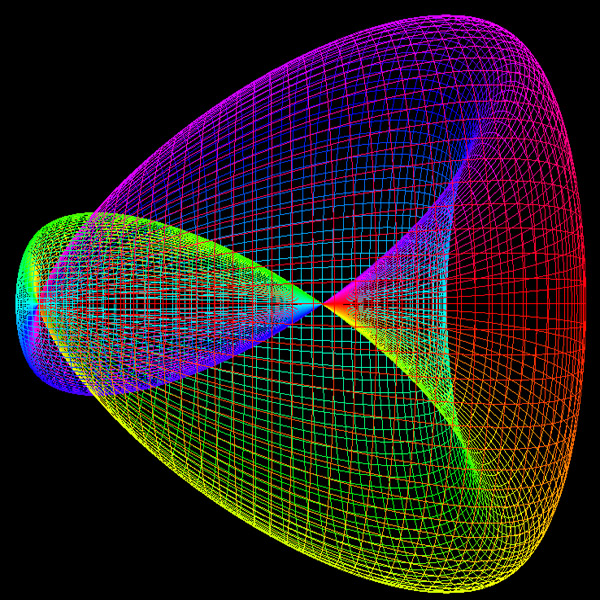
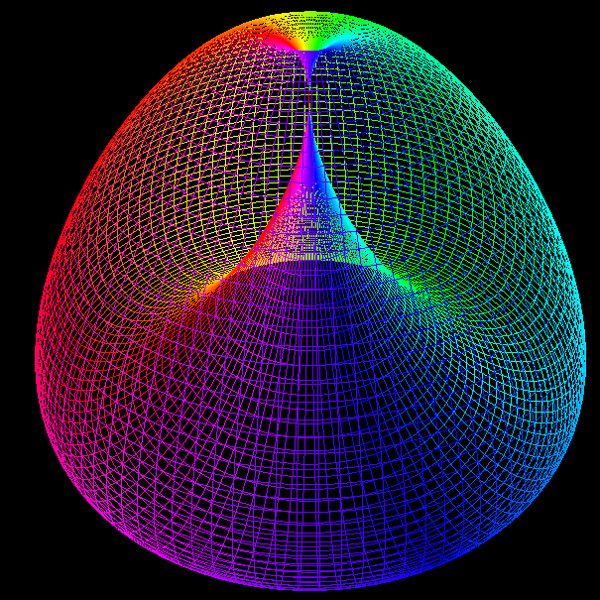
The Triaxial Tritorus is defined parametrically as
Where
Surface obtained by moving a circle that remains parallel to
a plane along a curve that is perpendicular to the same plane.
Attributed to Roger Bagula
PovRay scene:
doubletorus.pov
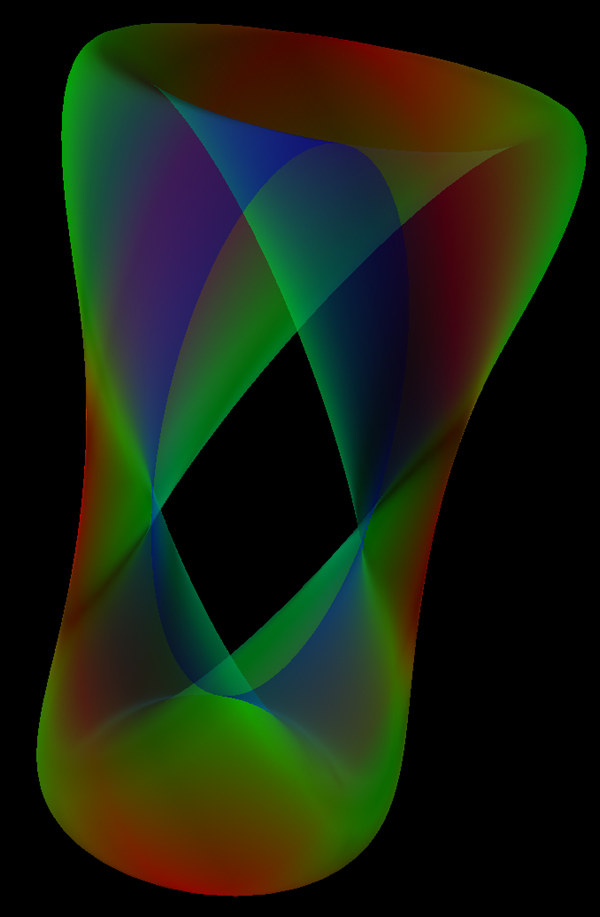
[ ((x-1)2 + y2 - c2)
((x+1)2 + y2 - c2) ]2 + z2 = d
(x2 (1-x2) - y2)2 + z2 = 0.01
August 2002
| ||||||||||||||||||||||||||||||||||||||||||||||||||||


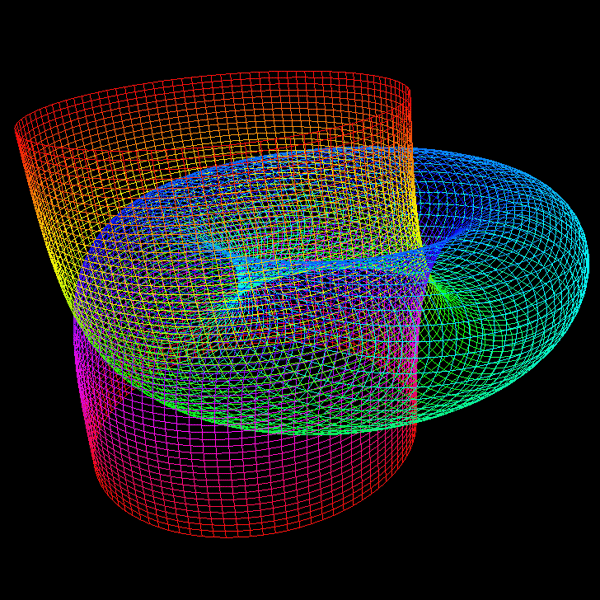
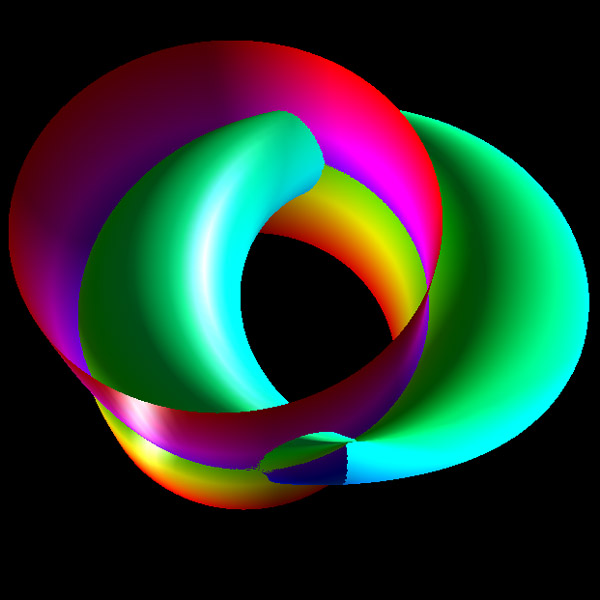

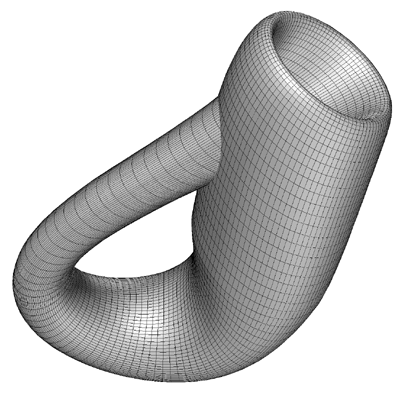
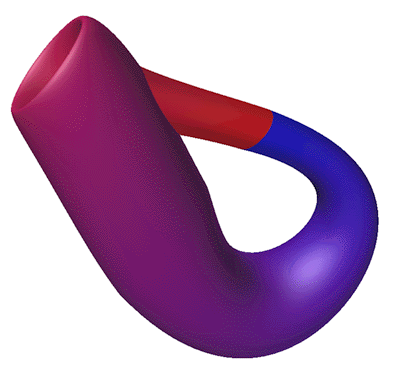
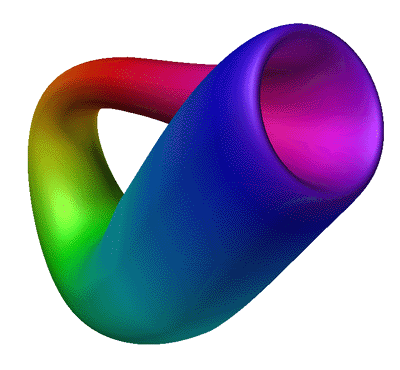 Featured in "mama 27", November 2000, pp 91, Figure 18.
Featured in "mama 27", November 2000, pp 91, Figure 18.


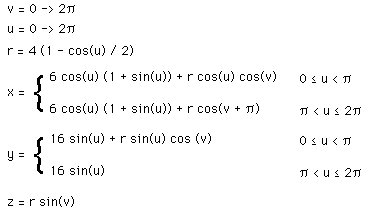
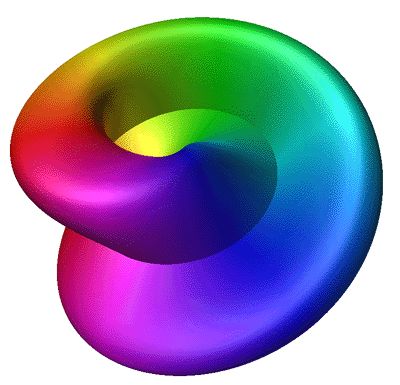









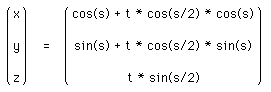
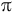 / 3)
(1 + cos(v + 2
/ 3)
(1 + cos(v + 2