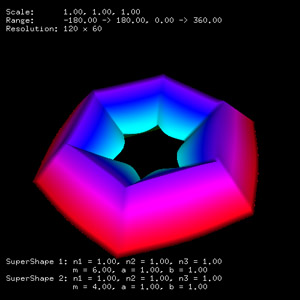
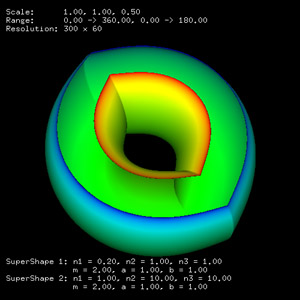
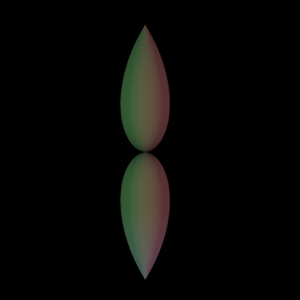
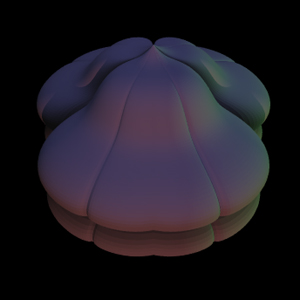
The supershape equation is an extension of the both the equation of the sphere and ellipse and even the superellipse given here. The general formula for the supershape is given below. 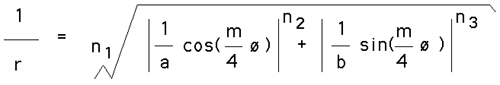
Where r and phi are polar coordinates (radius,angle). n1, n2, n3, and m are real numbers. a and b are real numbers excluding zero.
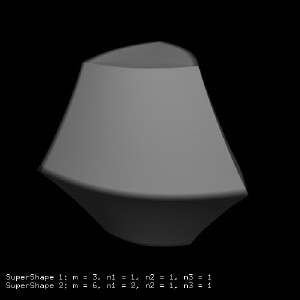
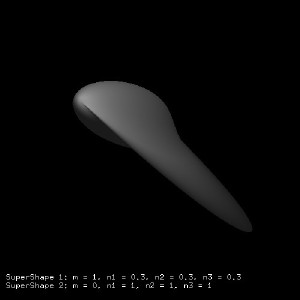
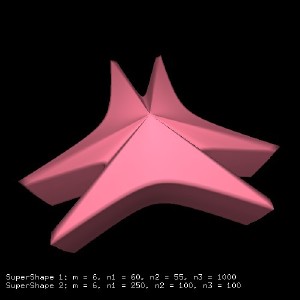
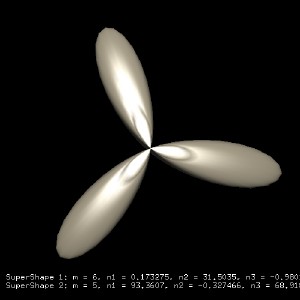
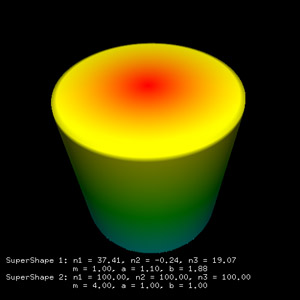
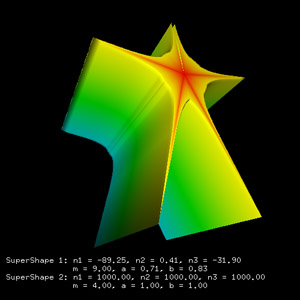
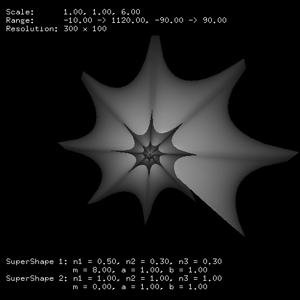
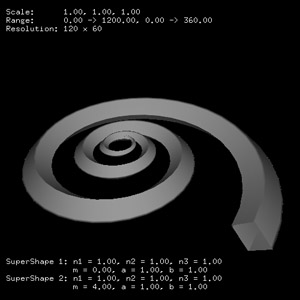
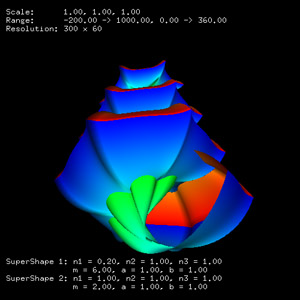
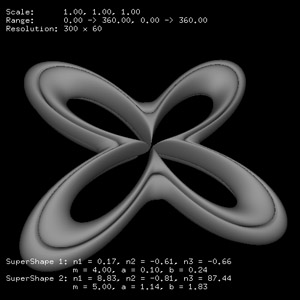
Other examples 






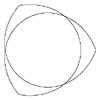
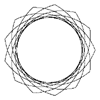
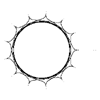
Given a value of phi the following function evaluates the supershape function and calculates (x,y).
void Eval(double m,double n1,double n2,double n3,double phi,double *x,double *y)
{
double r;
double t1,t2;
double a=1,b=1;
t1 = cos(m * phi / 4) / a;
t1 = ABS(t1);
t1 = pow(t1,n2);
t2 = sin(m * phi / 4) / b;
t2 = ABS(t2);
t2 = pow(t2,n3);
r = pow(t1+t2,1/n1);
if (ABS(r) == 0) {
*x = 0;
*y = 0;
} else {
r = 1 / r;
*x = r * cos(phi);
*y = r * sin(phi);
}
}
So it might be called as follows
Definition of supershape in 2 dimensions. 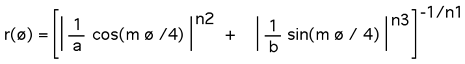
Extension to 3D using the spherical product. 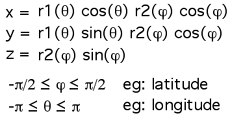
The following shows the interactive interface developed to explore 3D supershapes. It is
based upon X-Windows and OpenGL.
It is currently available for Mac OS-X (as a UNIX application). Use of the program is
straightforward, edit fields and hit return. The left mouse button rotates
the model in two axes, the middle mouse button rotates about the third
axis. A right mouse button brings up a menu.
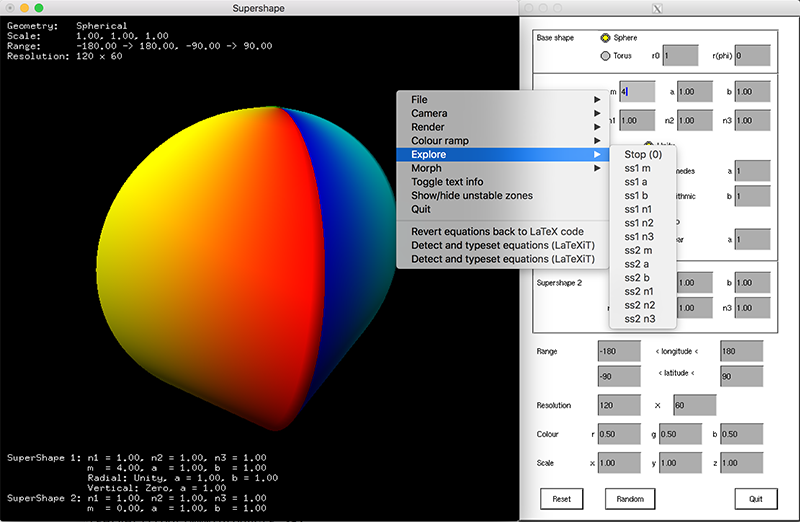 Click for full size image
Many settings can be initialised from the command line, others control is given by single key strokes. To see a complete list type the program name at the command prompt with a "-h" option. At the time of writing these are given below.
>supershape -h
Usage: supershape [command line options]
Command line options
-h this text
-f full screen
-s active stereo
-ss dual screen stereo
-a auto rotate
-rw wireframe
-rs flat shaded
-rp specular shaded
Mouse buttons
left camera rotate
shift left camera pan
middle camera roll
shift middle camera forward, reverse
Key Strokes
arrow keys camera rotate
<,> camera forward, reverse
+,- camera zoom in, out
[,] camera roll
r toggle window recording
w capture window to TGA file
a toggle auto rotation of camera
1,2,3 different rendering mode
h camera to home position
f1 to f6 axis aligned camera positions
ESC,q quit
Features
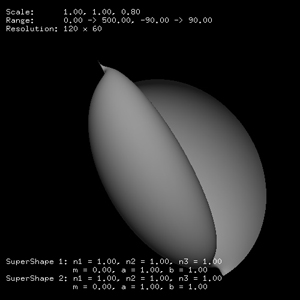
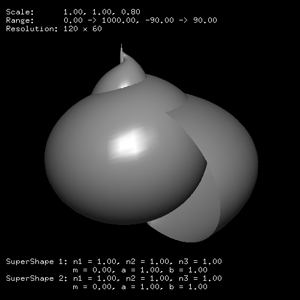
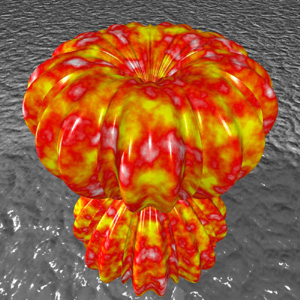
The 2D supershapes (but with added small thickness) can be created using this software by setting the second supershape parameters as m=0, n1=n2=n3=1, a=b=1 and using a small z axis scale factor. Indeed this can often be the preferred approach for using a 2D form within a 3D model, after all, real world objects do have some thickness. The example on the left has a thickness of 0.02 units (x and y axis dimensions of 1). Or even set the depth to 0 and vary latitude from 0 to 90 degrees as in the example on the right.
Extrusions of 2D supershapes can be created by setting the second supershape parameters as m=4, a=1, b=1, and high equal values for each of n1,n2,n3. For example n1=n2=n3=200 gives relatively sharp edges.
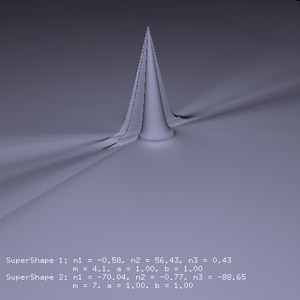
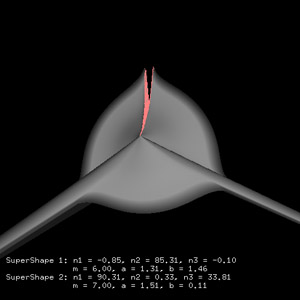
A significant portion of the parameter space results in surfaces with various types of numerical problems (powers of negative numbers, divide by 0, underflow, overflow, etc) as well as issues related to the representation of 3D graphics. The software that has been developed and created the images shown above, can display the edges where numerical problems have arisen. These regions are shown in pick as shown in the following two images.
The supershape function can obviously be modulated by another function. For example to create the shell like structures below, the radius (r1) of the superformula that varies the longitude is scaled by either a logarithmic or Archimedes spiral. In some cases the z coordinate is additionally made a linear function of longitude.
In the above the two supershapes were mapped onto a topological sphere. One could map supershapes onto other forms as well, for example, a torus. In the following images the mapping is as follows: 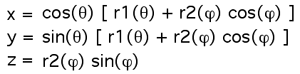

Generating the 3D Supershape in PovrayWritten by Paul BourkeJuly 2003
Based upon equations by Johan Gielis
There are two (at least) ways of representing supershapes using PovRay. One is to use the built-in parametric primitive, doing it this way would result in the highest resolution/quality results unfortunately the rendering times proved to be prohibitive. The approach illustrated below is to write a macro in the PovRay scene language. The macro and an example of it's use is given in this PovRay (version 3.5) file: supershape.pov.
Further POVRay scene examples are given below
Correspondence
Question: How can Superformula or Supershapes aid in data visualization? Do they help a person to gain a perspective of various data points? Are they better than pie-charts, graphs, histograms, scatter plots etc., Hmmm, they are kind of different things ... pie chart, graphs etc and supershapes. In the former one takes data and uses it to control some geometry, quite simple geometry like portions of a pie, height of bars, points on a plane, lines and so on. The resulting structure is intended to provide some insight into the underlying data. At the end of the day the purpose of visualisation is to provide insight and the success of a visualisation should be judged as such. Supershapes are (complex) 3D surfaces, they came about because Johan thought they could be used to describe a large range of biological shapes, namely leaves, flowers. The big problem with supershapes is the relationship between the variables and the final form is not always clear. So, if you gave someone a geometric form and asked what the variables are to represent that as a supershape, it is difficult, most people just play/fiddle and hope for the best. Perhaps you are imagining mapping data to the variables and using the resulting supershape as a visualisation of the data. There may be some datasets for which this might work, but I doubt it. For the same reason, the relationship between the variables and the shape is unclear. And, if you have two very similar datasets the supershape could look very different ... not a good property for a visualisation. |
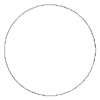
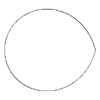 m=2
m=2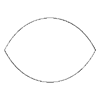
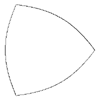 m=4
m=4
 m=6
m=6
 m=2
m=2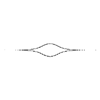
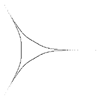 m=4
m=4
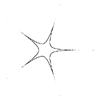 m=6
m=6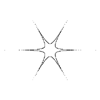
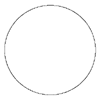 m=2
m=2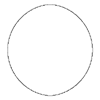
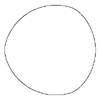 m=4
m=4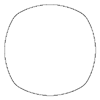
 m=6
m=6
 m=4
m=4
 m=6
m=6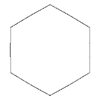
 m=4
m=4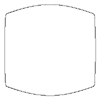
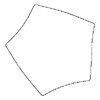 m=6
m=6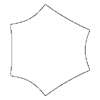
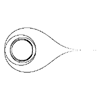 m=7/6
m=7/6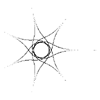
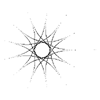 m=19/6
m=19/6
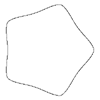 n1=0.20
n1=0.20
 n1=0.02
n1=0.02