HyperboloidWritten by Paul BourkeFebruary 2024
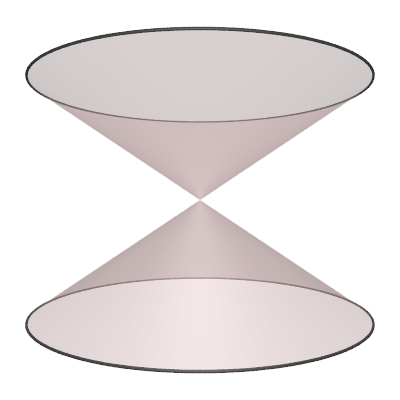
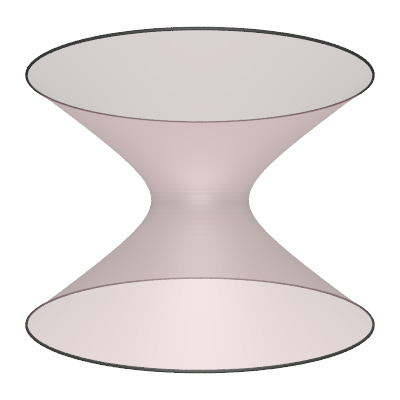
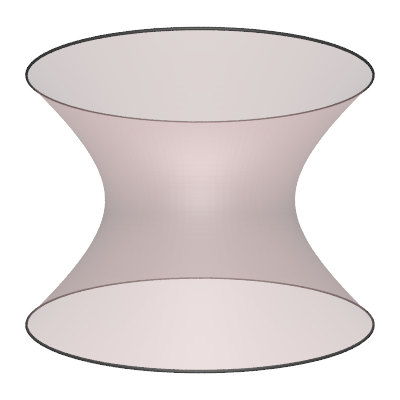
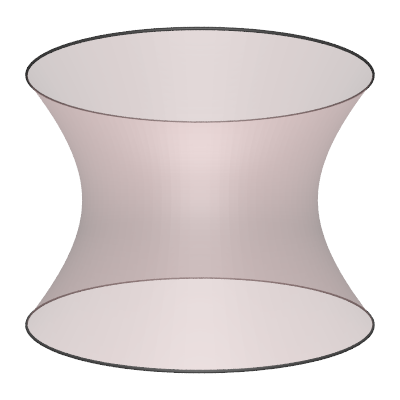
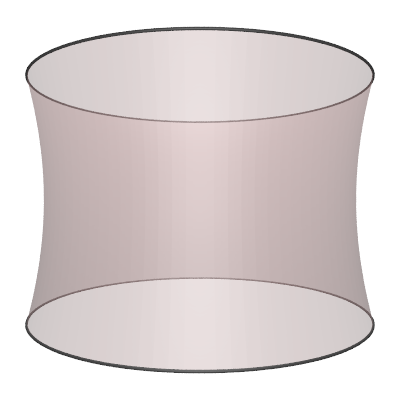
The hyperboloid is the surface of revolution of the 2D hyperbola. 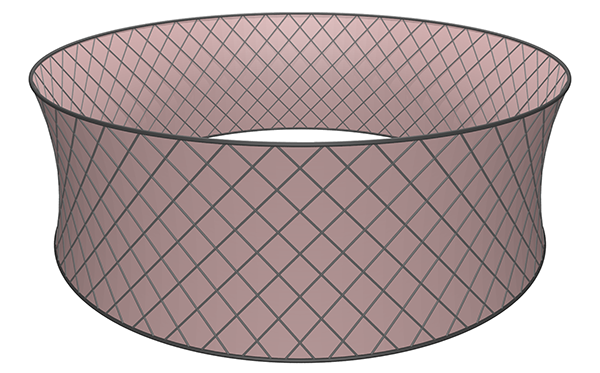
The parametric expression for the hyperboloid (in one sheet) with radius "r" and height "h" is as follows 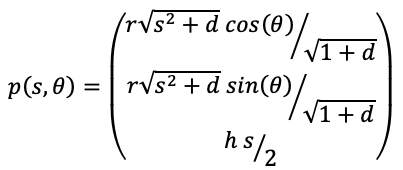
where -1 <= s <= 1 and 0 <= θ <= 2π. Various values of parameter "d".
As a practical example, 360 panorama screens generally involve an elastic material tensioned between an upper and lower ring. The minimum energy form for this is a hyperboloid, see simulation below for the Murten panorama. 
A consequence of this is that the panorama material once removed from the rings can no longer be laid flat on the floor. |