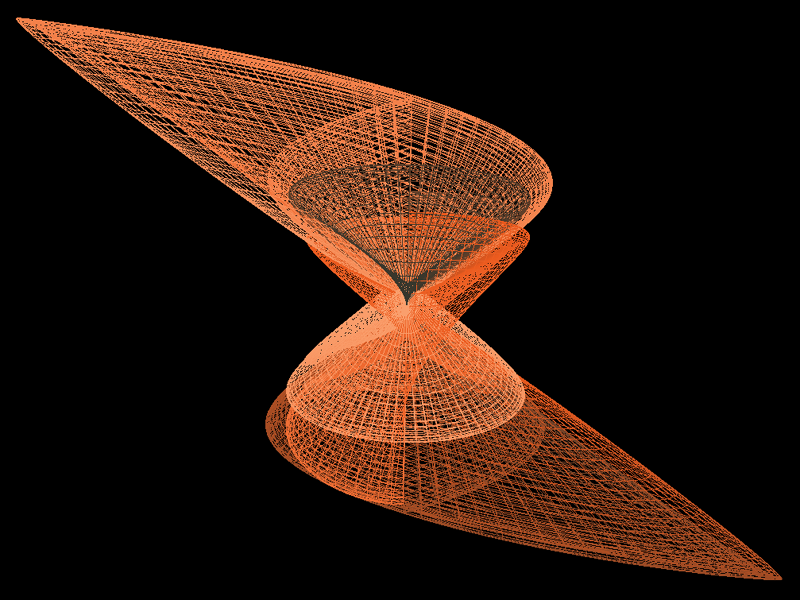
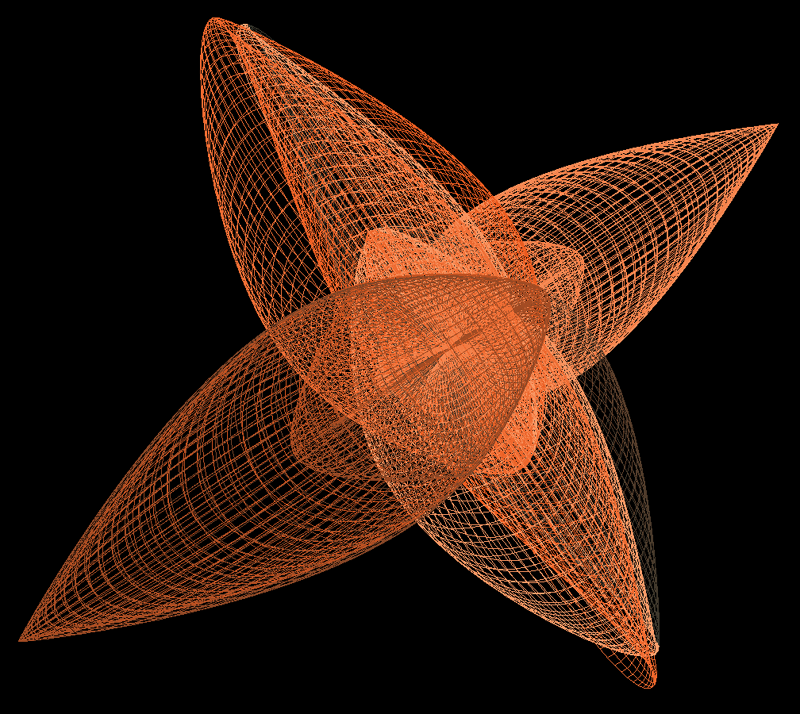
Fano planesContribution by Roger BagulaC code and renderings by Paul Bourke January 1999
SET MODE "color"
SET WINDOW 0, 1026,0,750
SET COLOR MIX(1) 0,0,0
PRINT" Fano Plane cosine function projection"
PRINT" by R. L. Bagula 7 Sept 2000©"
LET s1=250
FOR t= 0 to 1 step 1/200
LET count=count+1
FOR p= 0 to 2 step 1/600
LET a1=2*pi*(t-p/3)
LET b1=2*Pi*(-t-p/3)
LET c1=2*Pi*(t-sqr(3))
LET x=cos(a1)*COS(b1)*cos(c1)
LET y=cos(2*pi*(t-p/3+2/3))*COS(2*Pi*(-t-p/3+2/3))*cos(2*Pi*(-t-p+1))
LET Z=cos(2*pi*(t-p/3-2/3))*COS(2*Pi*(-t-p/3-2/3))*cos(2*Pi*(-t+p+1))
SET COLOR 256-mod(count,256)
PLOT 1026/4+s1*x/(1+Z/4),750/4+s1*(750/1026)*y/(1+Z/4)
PLOT 1026/1.5+s1*Z/(1+y/4),750/1.5+s1*(750/1026)*x/(1+y/4)
SET COLOR 1
NEXT p
PLOT
NEXT t
END
C Code by Paul Bourke
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "paulslib.h"
XYZ Eval(double,double);
#define Nx 200
#define Ny 200
int main(int argc,char **argv)
{
int i,j,k,icolour = 9;
double t,p,dt,dp;
XYZ q[4],q1,q2,n[4];
COLOUR colour;
if (argc > 1)
icolour = atoi(argv[1]);
dt = 1 / (double)Nx;
dp = 2 / (double)Ny;
for (i=0;i<Nx;i++) {
t = i * dt;
for (j=0;j<Ny;j++) {
p = j * dp;
q[0] = Eval(t,p);
n[0] = CalcNormal(q[0],Eval(t+dt/10,p),Eval(t,p+dp/10));
q[1] = Eval(t+dt,p);
n[1] = CalcNormal(q[1],Eval(t+dt+dt/10,p),Eval(t+dt,p+dp/10));
q[2] = Eval(t+dt,p+dp);
n[2] = CalcNormal(q[2],Eval(t+dt+dt/10,p+dp),Eval(t+dt,p+dp+dp/10));
q[3] = Eval(t,p+dp);
n[3] = CalcNormal(q[3],Eval(t+dt/10,p+dp),Eval(t,p+dp+dp/10));
colour = GetColour((double)i,0.0,(double)Nx,icolour);
printf("f4n ");
for (k=0;k<4;k++)
printf("%g %g %g ",q[k].x,q[k].y,q[k].z);
for (k=0;k<4;k++)
printf("%g %g %g ",n[k].x,n[k].y,n[k].z);
printf("%g %g %g\n",colour.r,colour.g,colour.b);
}
}
}
XYZ Eval(double t,double p)
{
double a,b,c;
XYZ q;
a = TWOPI * (t - p/3);
b = TWOPI * (-t - p/3);
c = TWOPI * (t - SQRT3);
q.x = cos(a) * cos(b) * cos(c);
q.y = cos(TWOPI*(t-p/3+2/3))*cos(TWOPI*(-t-p/3+2/3))*cos(TWOPI*(-t-p+1));
q.z = cos(TWOPI*(t-p/3-2/3))*cos(TWOPI*(-t-p/3-2/3))*cos(TWOPI*(-t+p+1));
return(q);
}
|