Symmetry in ChaosWritten by Paul BourkeMarch 2023
The following is based upon systems of equations found in "Symmetry in Chaos, A Search for Pattern in Mathematics, Art, and Nature" (the second edition) by Michael Field and Martin Golubitsky. They ask the question whether there are aperiodic chaotic attractors that generate symmetric patterns? Can there be order within chaotic systems?  Shield
The attractors are based upon the following formula for the m+1'th term in the series given 5 parameters a0 a1 ... a4. The integer n is the degree of symmetry. The z is complex valued and all an are real valued.
Many of the examples presented here are named as published in the book and by other experimenters. The parameters a0 a1 ... a4 for some are provided in the book and subsequent papers, where they are denoted as lambda, alpha, beta, omega and gamma respectively.  Kachina Dolls
The images here are generated by iterating the series typically 1,000 million times. This is performed in two passes, the first pass with many fewer iterations is used to find the bounds of the attractor on the complex plane, the second pass actually "draws" the attractor points. The process of drawing involves treating the bounded region of the complex plane as a 2D histogram, each time the series passes through a pixel region on the plane the histogram at that location is incremented. One might imagine the 2D histogram as a height field, a larger values at a point indicate that the complex series passed through that pixel more often than a point with a smaller value. At the end of the process the histogram is mapped onto colours depending on the histogram values, there are many ways to do this based on aesthetic grounds.  Emperors Cloak
A rough guide to parameters.
 Santa Chiara
Unfortunately, for a system of equations with 6 parameters and therefore a large parameter space, the set of parameters that yield "interesting" results is quite small.
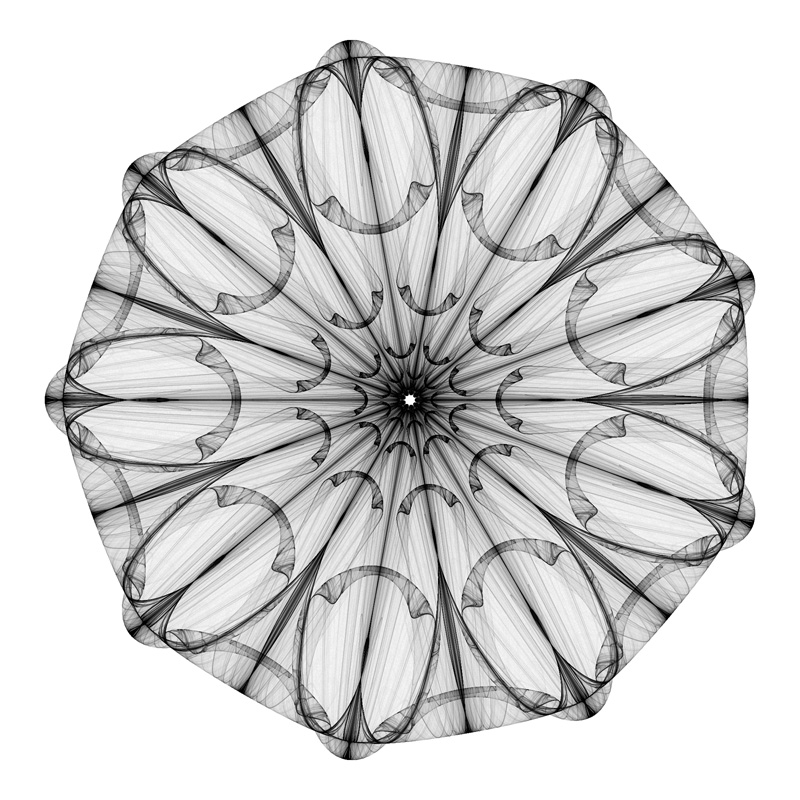 French Glass
 Halloween
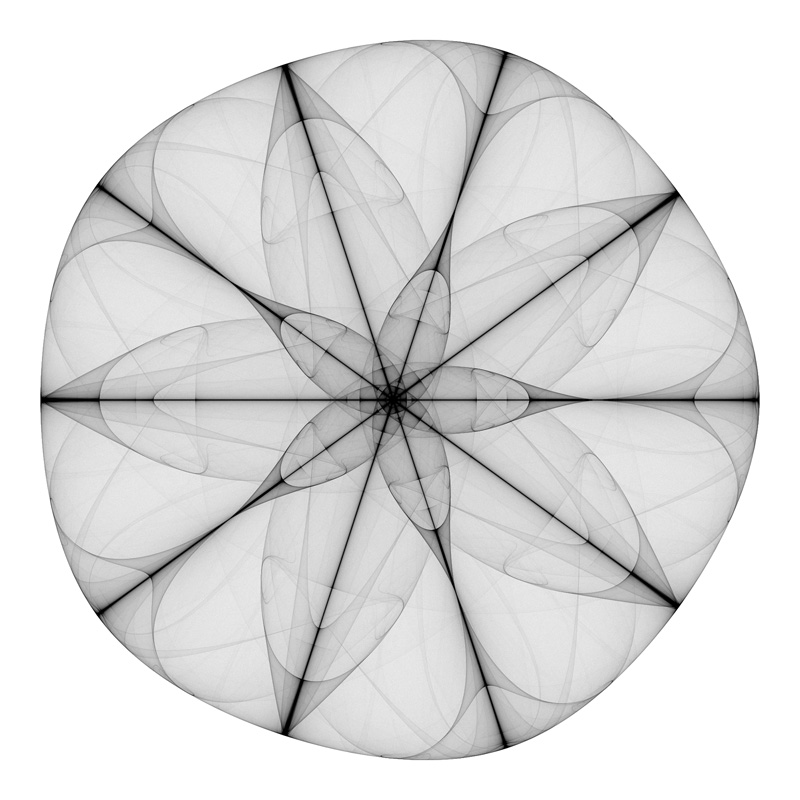 Pentium
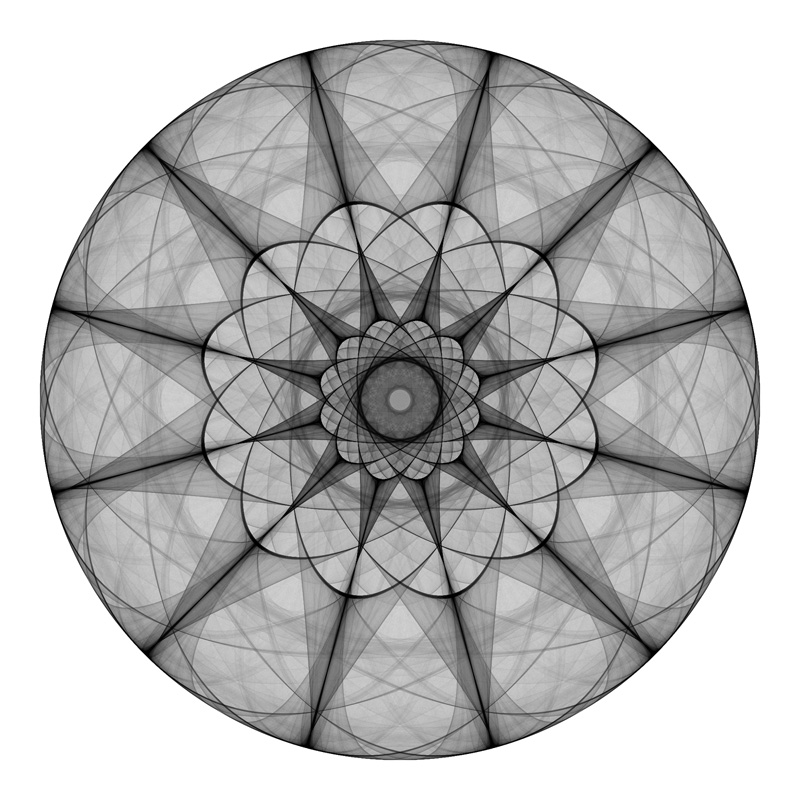
 Fish and eye

A modified equation is also presented from the book as follows. 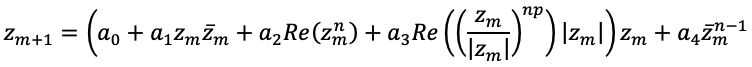
 Gothic Medallion
 Mercedes-Benz
 Sunflower
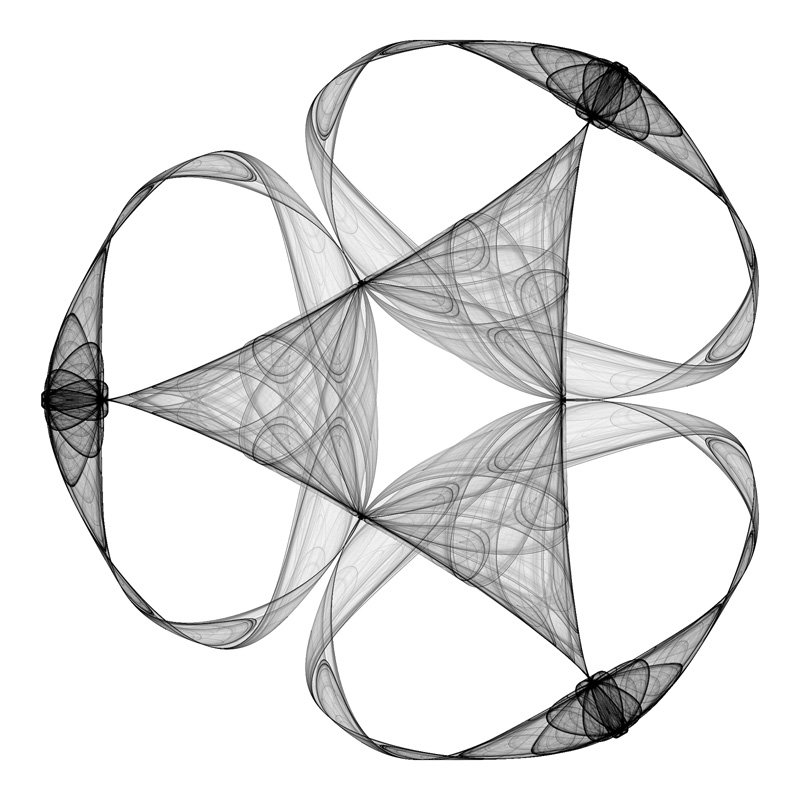
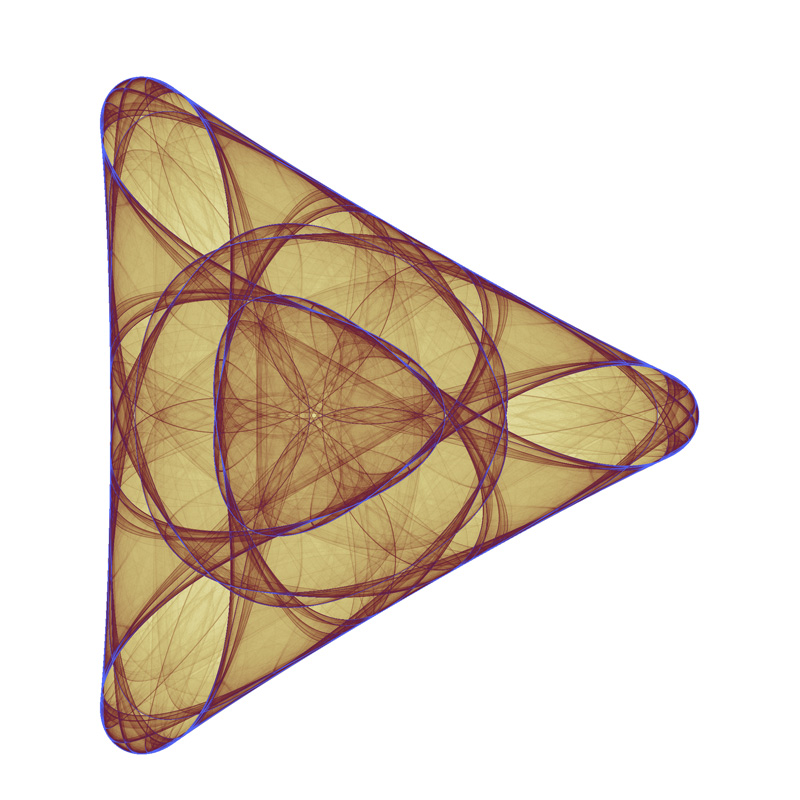
Random parameter search.  6 fold symmetry
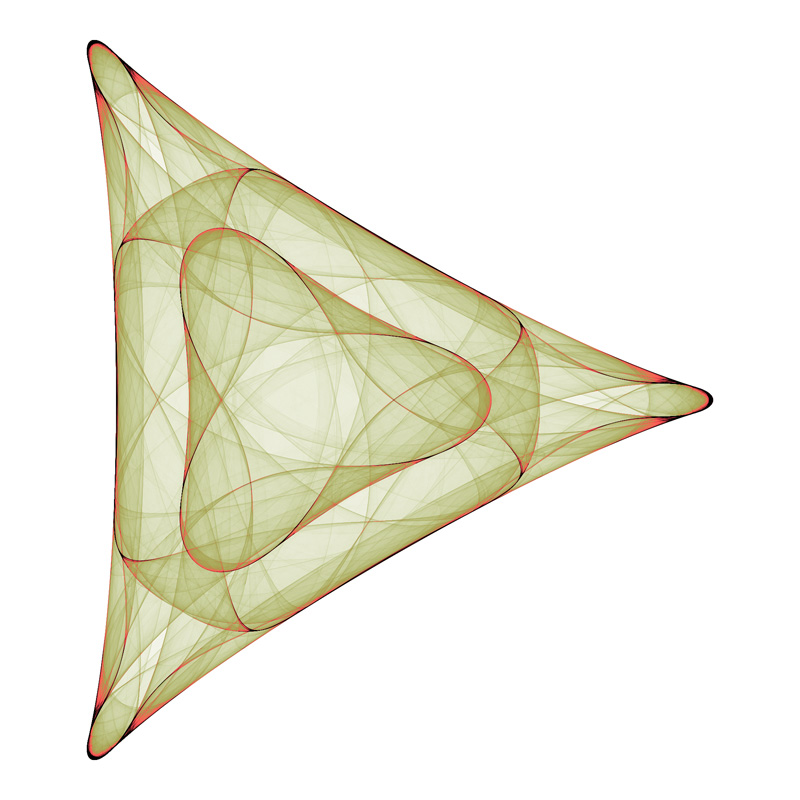
 3 fold symmetry
 6 fold symmetry
Cases with both mirror and orientation symmetry, omega=0.  6 fold symmetry
 3 fold symmetry
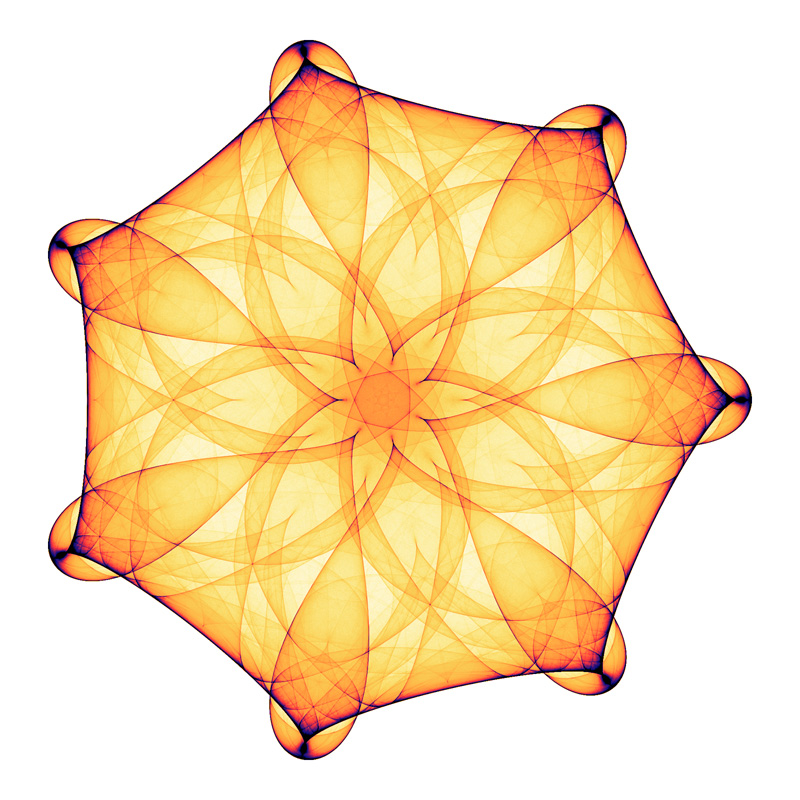
8 and 12 fold symmetry tables.    8 fold symmetry
   12 fold symmetry

References
|