Julia set of sin(z)Written by Paul BourkeMay 1998, updated examples in 2019 Python generator: julia_set.py by Tim Meehan. The following illustrates the Julia set for functions of the form
where z is a complex number x + iy. To do this we form the series
starting with some initial z0 The behaviour of this series determines whether or not the initial z0 is part of the julia set or not. More precisely, if the series tends to infinity then z0 is part of the Julia set, otherwise it isn't. In the examples shown on the right the white regions are in the Julia set, black points are outside the Julia set. To create images of the Julia set we map pixels in the image onto values of z0 and colour the pixel dependent on the behaviour of the series. In the examples on the right the image is mapped onto the range +-2pi in both the real and imaginary axes. The series is tested after 50 terms, it is decided that it tends to infinity if the absolute value of the imaginary part of zk is greater than 50. FootnoteIf you are wondering how to compute the sine of a complex number, you can use the following relationships: yk+1 = cos(xk) sinh(yk) where zk = xk + i yk
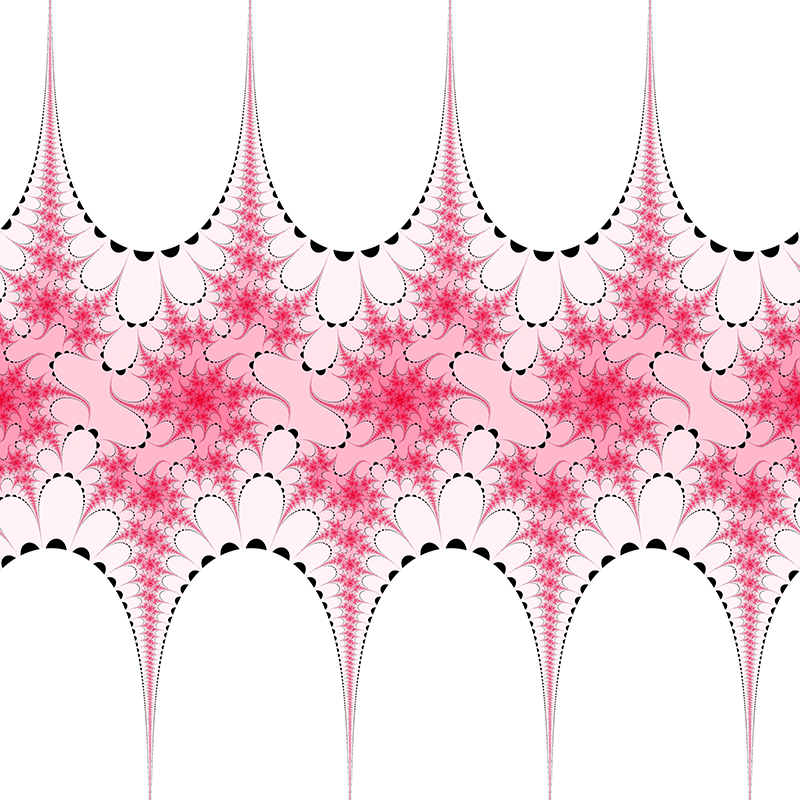 c = 1 + i 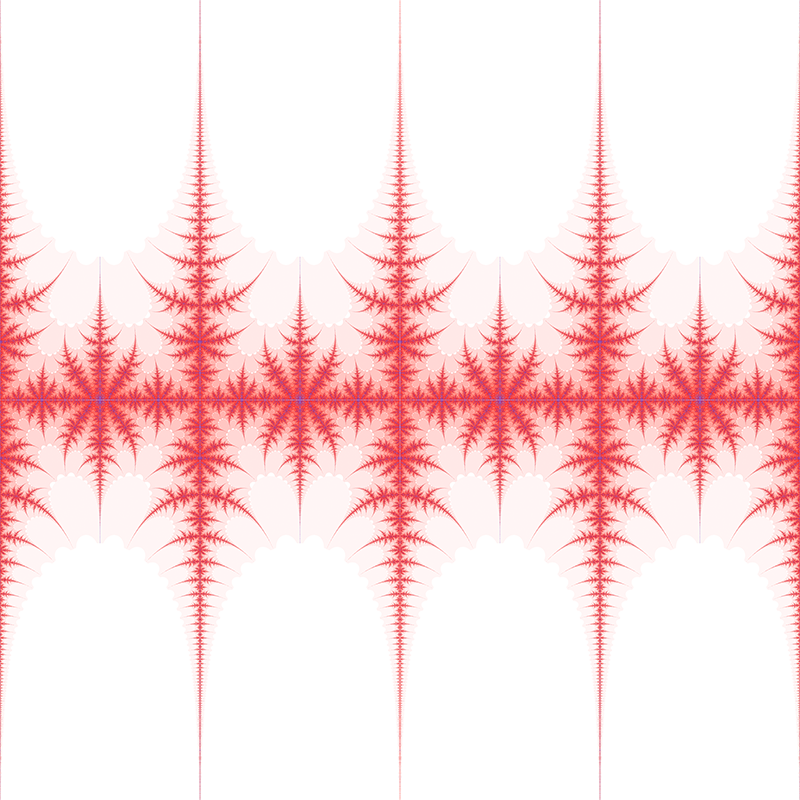 c = 3i/2 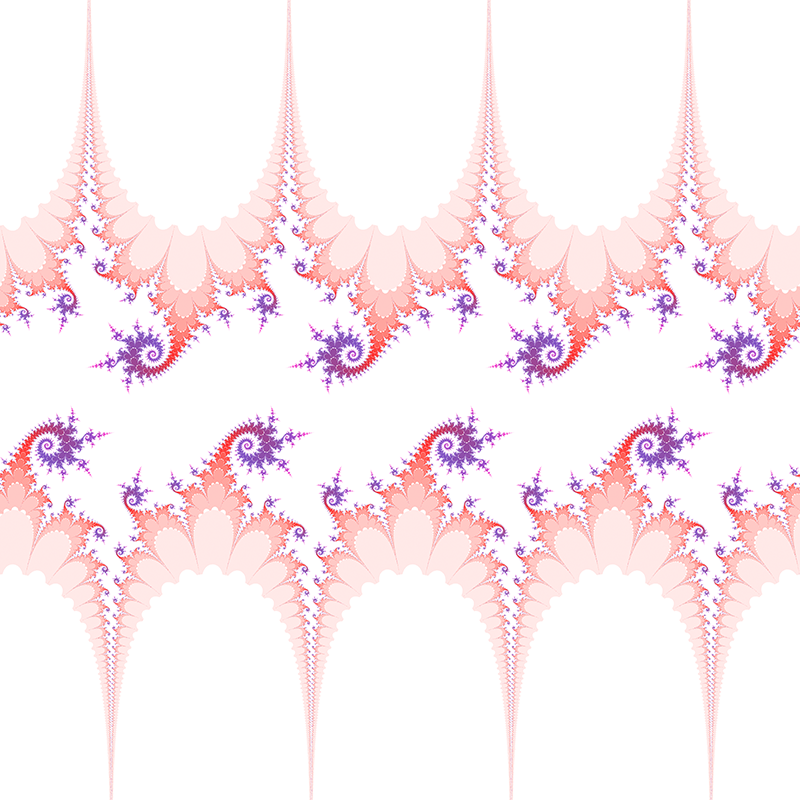 c = 0.984808 + 0.173648i 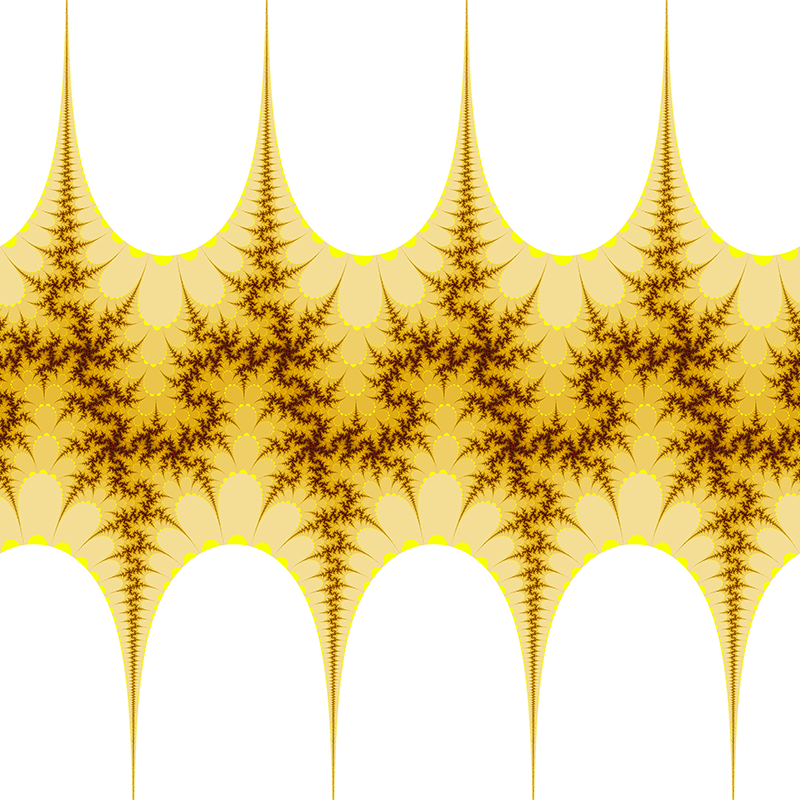 c = -1.29904 + -0.75i 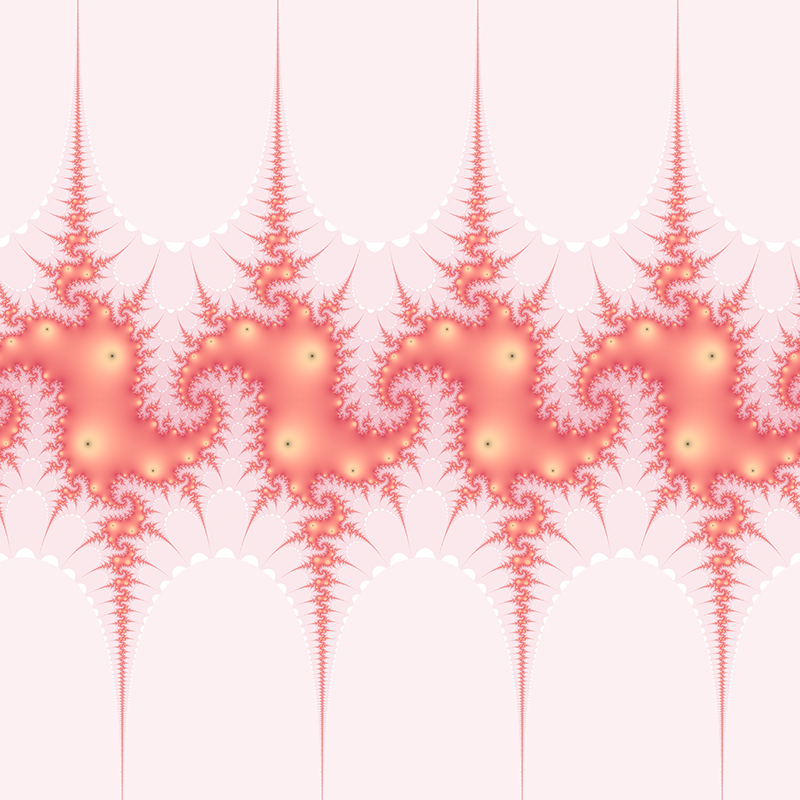 c = 1.17462 + 0.427525i 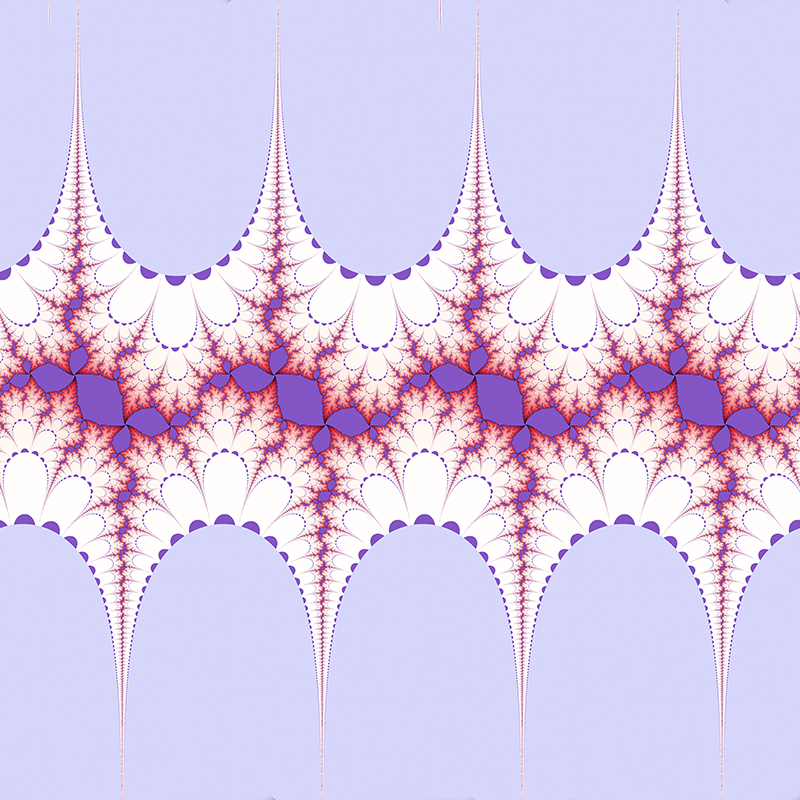 c = 1.87939 + 0.68404i 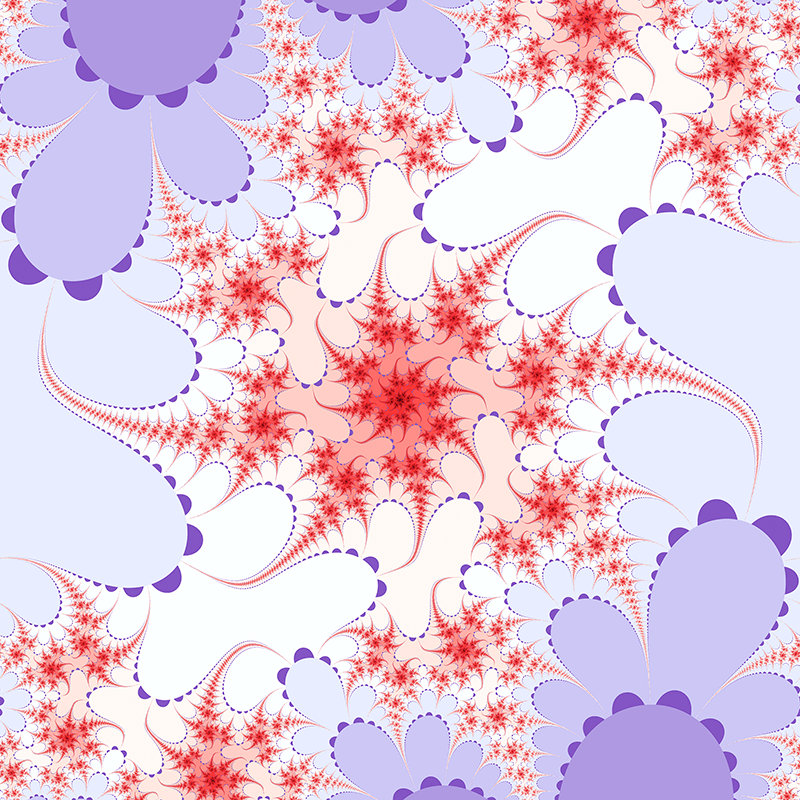 c = 1 + i  c = -0.2 + i      Contributions by Klaus Messner
 c = 1 + 0i x = -1.201171875, y = -0.963541666666666  c = 0 + i x = -0.5390625, y = -1.4296875 |





