Multifractal Julia fractalsWritten by Paul BourkeApril 2005 Inspired by work by Roman Nosov
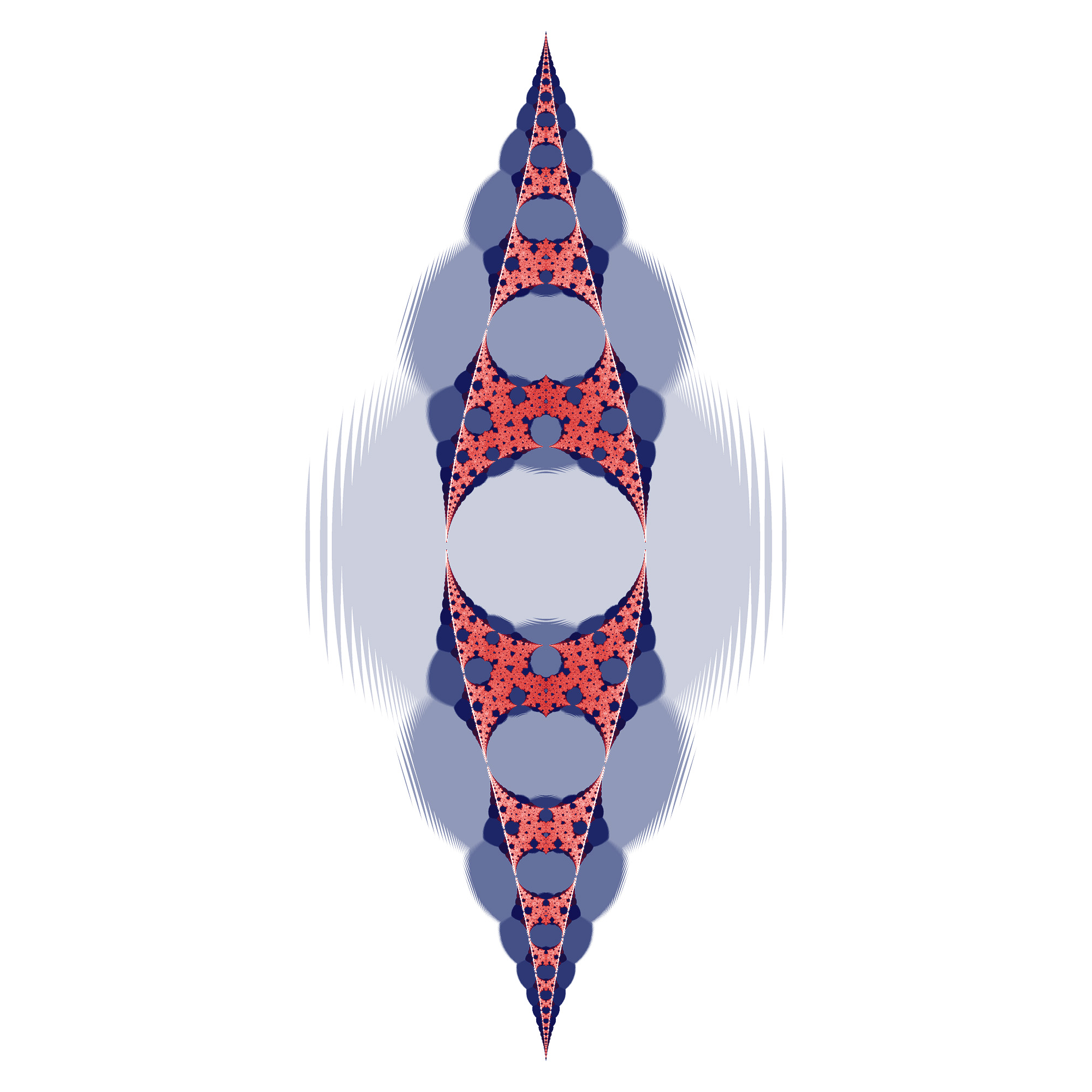
The images here are created by studying the complex values series of the form shown below.
zn+1 = c zn-2 + c zn+1 = c2 zn-2 + c zn+1 = c-1 zn-2 + c
Where z0 = 0, and c is taken as the point on the complex plane currently under consideration (it will be coloured depending on the behaviour of the series). These series evolve in a number of ways, for points in the complex plane away from "the action" the series remains constant. For interesting points (values of c), the series is periodic. It is the period of this series that is generally mapped to colour. 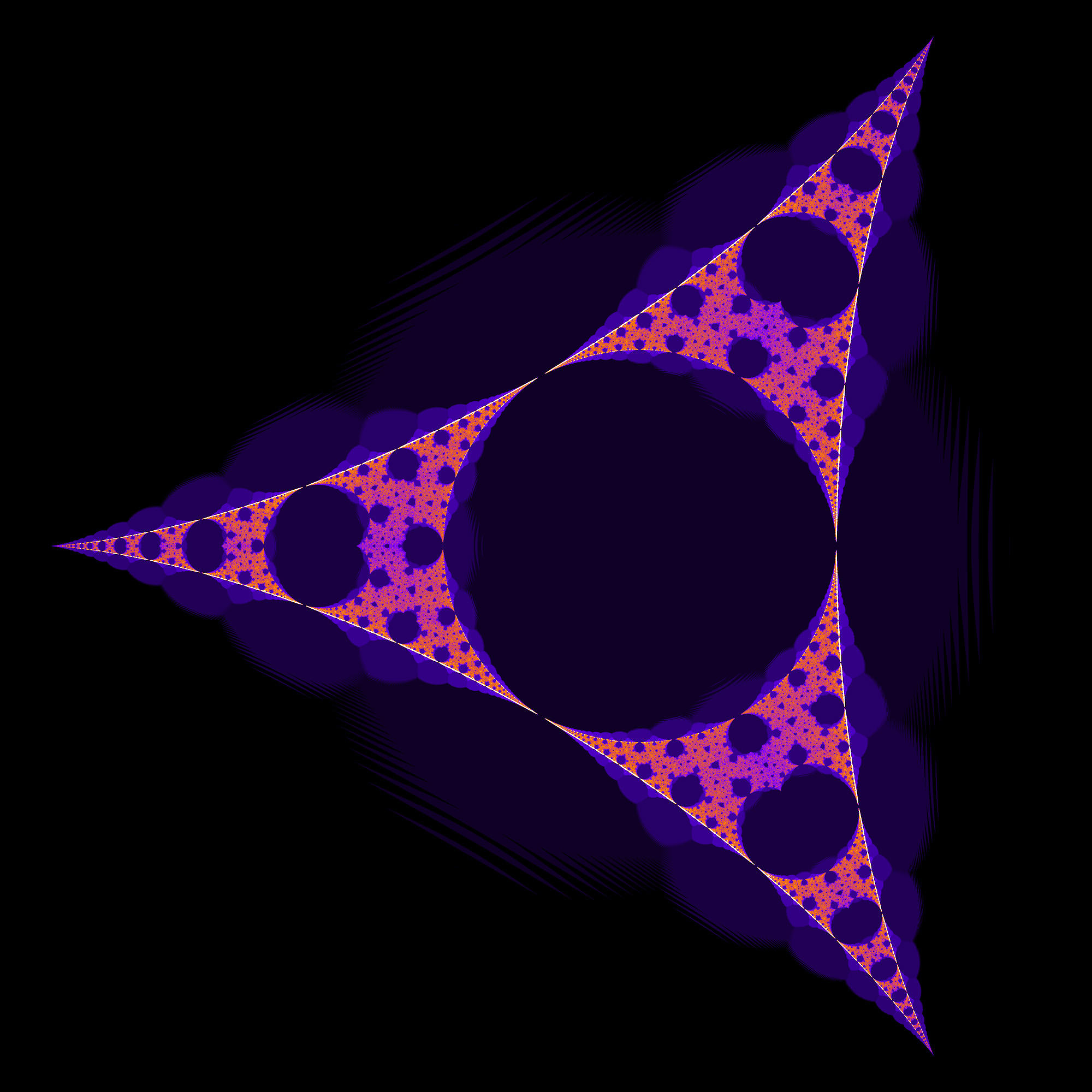

|