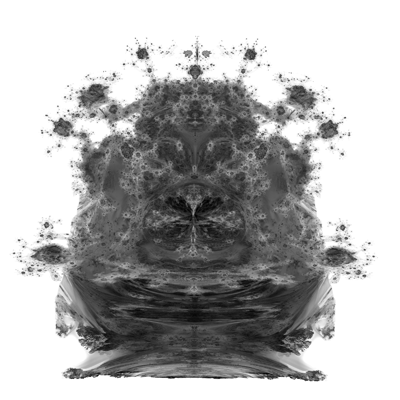
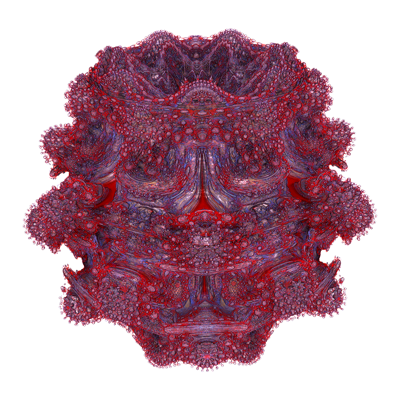
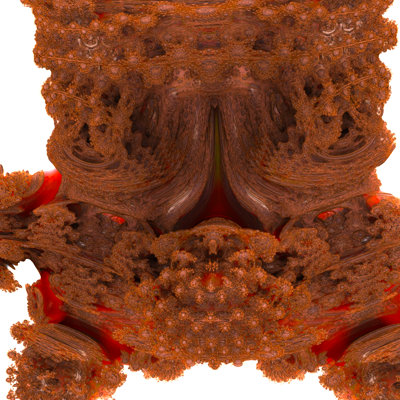
Mandelbulb setInspired by equations by Paul Nylander
Written by Paul Bourke
The so called Mandelbulb is a 3 dimensional fractal created by performing the standard Mandelbrot calculation for the series
for each point P0 within 3D space, and where the square of "P" is defined as 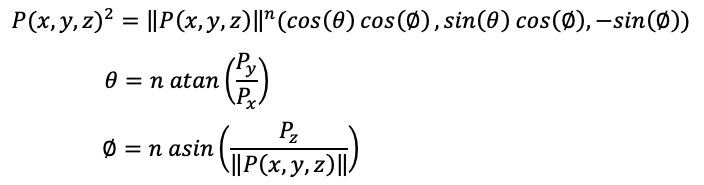
This formulation is credited to Daniel White and Paul Nylander using spherical coordinates, the original description credited to Jules Ruis. n = 0 This is an empty set.n = 1 The set is just a line along the z axis. n = 2 (See Quadratic Mandelbrot)
n = 3
n = 4
n = 5
n = 6
n = 7
n = 8 - The most commonly implemented power
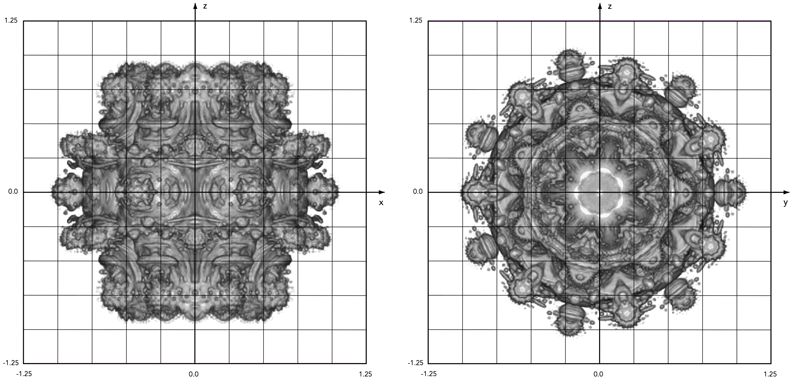
n = 10
n = 20
There is nothing in the mathematics that restricts "n" to an integer value. n = 1.75
n = 4.5
n = 5.8
The mathematics is also not limited to positive n. n = -4
z axis cross sections.
The following is the usage string for the utility that creates a volume containing a part of a Mandelbulb and exports the data for a volume visualisation software. Usage: bulb [options] n Options: -a n Antialiasing level, default: 2 -o x y z Origin coordinates, default: 0 0 0 -n x y z Voxels on each dimension, default: 100 100 100 -r n z axis range about orgin, default: 1.25 -p n power of the MandelBulb, default: 8 -i n maximum number of iterations, default: 255
|