"Having a bad hair day" attractorWritten by Paul BourkeAugust 2021 Inspired by Antonio Sánchez
The images on this page are created using the equations below. They represent a patch of the x-y plane, typically centred on the origin, showing each point (xn, yn) in the series. 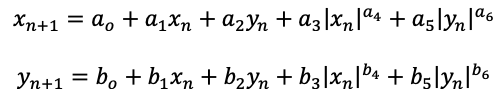
The equations were sourced from an article by Antonio Sánchez titled "Strange Attractors: an R experiment about maths, recursivity and creative coding". In that article the attractor is under the section titled "The General 2D-Map". The name given here is inspired from the appearance of the first and last image below. In general the series can behave in one of four ways depending on the values of the 14 parameters. It can converge to a fixed point, diverge to infinity (the most common), or form a periodic limit cycle. The images here are the fourth option where none of the other three occurs. While the parameter space is large (14 dimensions), most of the interesting chaotic attractor behaviour occurs for values of the parameters between -2 and 2. Related work by the author can be found here: Random Attractors. A similar approach was used here to identify "interesting" attractors from the large possible parameter space. The original exploration of polynomial attractors can be found here: Polynomial attractors credited to J.C.Sprott.
 1.1, -0.3, -0.1, 0.6, -1.2, -0.7, 0.2, 1.4, 1.4, 0, -0.3, -0.5, -1.1, -0.5
 -0.8, 0.4, -1.1, 0.5, -0.6, -0.1, -0.5, 0.8, 1.0, -0.3, -0.6, -0.3, -1.2, -0.3
 -1.2, 0.1, -0.1, -0.6, 1.2, -0.4, -0.9, -0.2, -1.2, -1.2, -0.6, 0.4, 0.7, -0.7
 0, -0.9, -0.7, -1.3, 0.5, -0.6, -0.5, -0.3, 1.4, 0.2, -0.6, -1.3, -0.3, -0.9
 0, -0.8, 1.1, 1.1, 0.7, -0.4, 0.4, -1.4, -1.1, 0.3, 0.3, -1, -0.5, 0.8
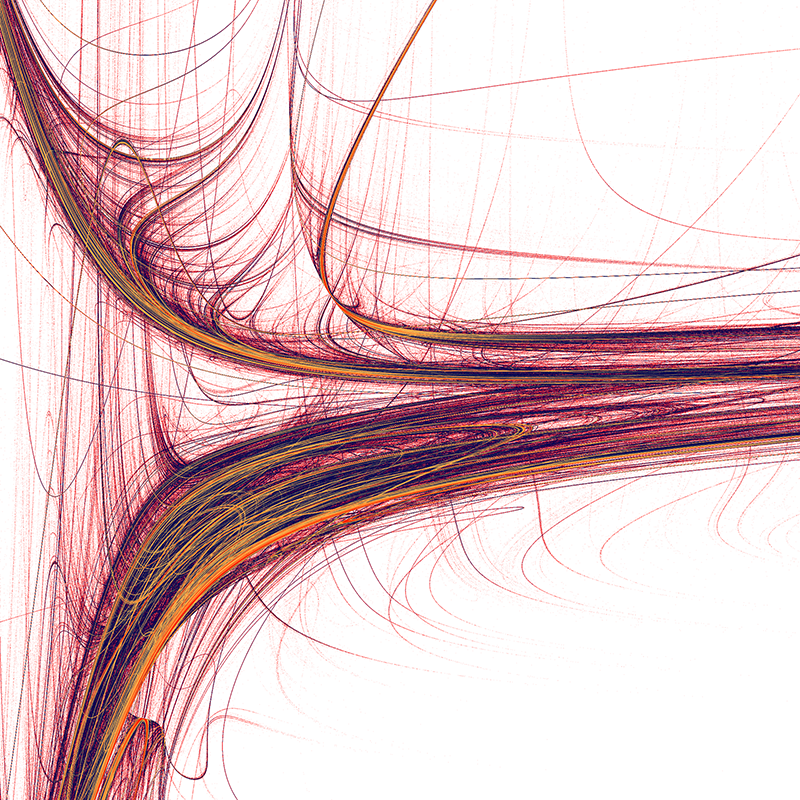
 -0.3, -0.57, 0.52, -0.71, -0.39, -0.36, -0.53, -0.07, -0.18, -0.95, -0.12, 0.93, 0.16, 0.37
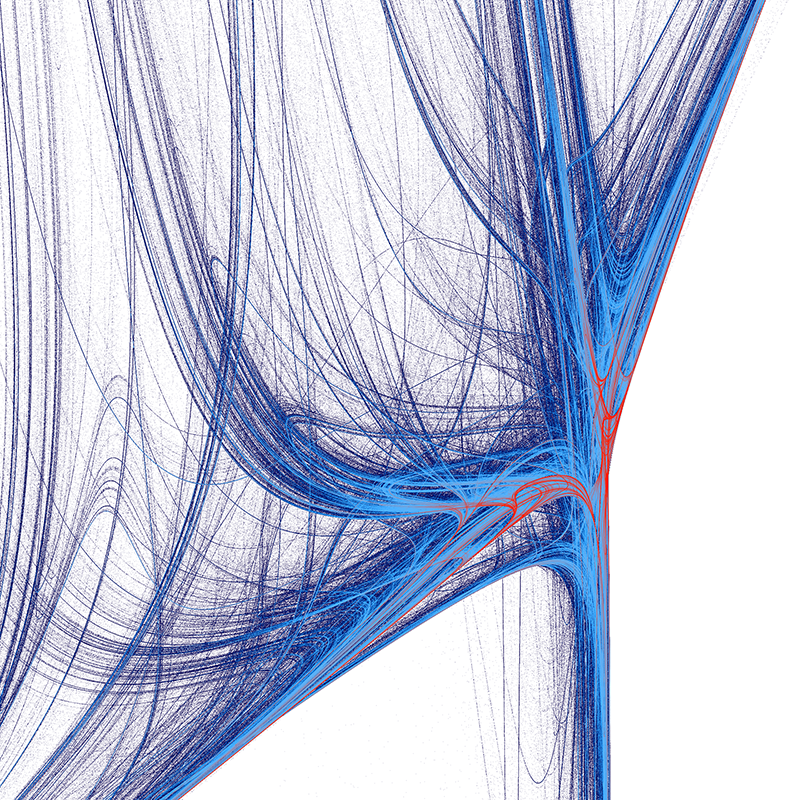 0.78, 0.06, 0.81, -0.11, -0.92, -0.71, 0.8, 0.57, 0.02, -0.9, -0.77, -0.93, 0.2, -0.77
 -0.61, 0.35, 0.93, 0.64, 0.61, -0.95, 0.49, -0.88, -0.4, 0.53, 0.79, -0.99, 0.28, 0.05
 -0.71, -0.56, -0.54, -0.97, -0.43, 0.85, 0.86, 0.59, 0.88, -0.83, -0.85, 0.97, -0.17, -0.45
 0.45, 0.36, -1.23, 0.55, -0.32, 0.45, -1.43, 1.43, 0.77, 0.1, 1.07, -0.94, 0.63, 0.52
 -0.208, 0.929, -0.717, 0.010, 0.501, -0.170, -0.611, 0.599, 0.868, 0.405, -0.148, -0.792, 0.691, 0.161 Parameters courtesy of Juan José Salinas Catrián
 -0.22, -0.74, 0.83, -1.11, 0.18, 0.21, -0.74, 1.2, -1.33, 0.49, 0.54, -0.97, -0.84, -0.43
 -1.14, -0.96, -0.31, -0.33, -0.89, 1.42, 0.64, -1.18, 0.98, -0.17, 0.02, 0.83, -1.35, -0.25
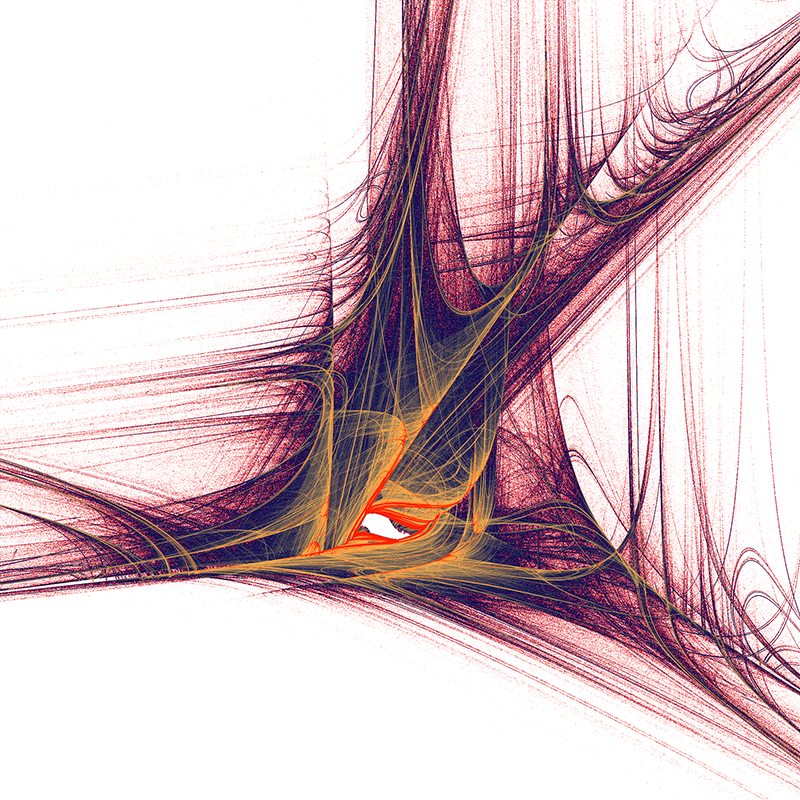 -0.33, -0.19, 0.57, 1.22, 0.93, -0.56, -0.16, -0.03, -0.87, -0.06, -0.97, 0.62, -1.28, -0.85
|