The following illustrates three ways (from an infinite set) by which a planar image can be projected onto a fisheye for projection into a planetarium. The very specific options shown here are chosen as suitable ways of displaying 2 dimensional slides for a planetarium presentation, for example slides from a package such as KeyNote or PowerPoint. The goal is to make the 2D slide look as though it is actually sitting on a plane rather than wrapped around in dome space. As such the three orientations for the plane are shown on the right. In the first one imagines an upright wall with the 2D image painted on it, while this is a nice effect it has the problem of reduced resolution near the top of the image which is likely to be exactly where slide titles and the important information resides. The second and third cases have the plane rotated at 45 and 30 degrees respectively, the height of the panel is set so that it just appears above the horizon (in the examples here the image proportions are assumed to be 4:3). In all these cases while the text appears curved in fisheye space, it should look straight in the dome as should the frames of the plane.

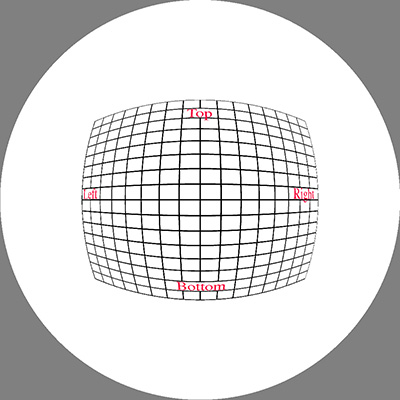
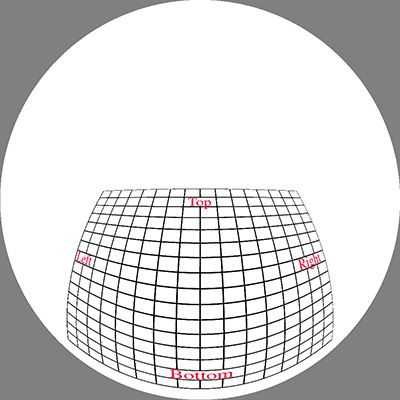
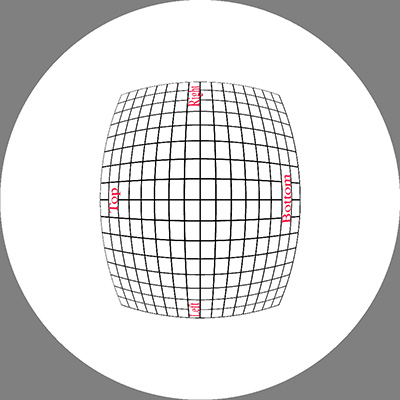
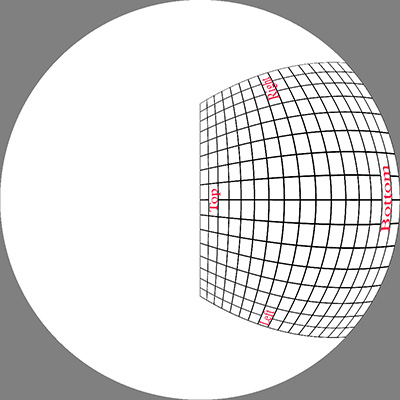
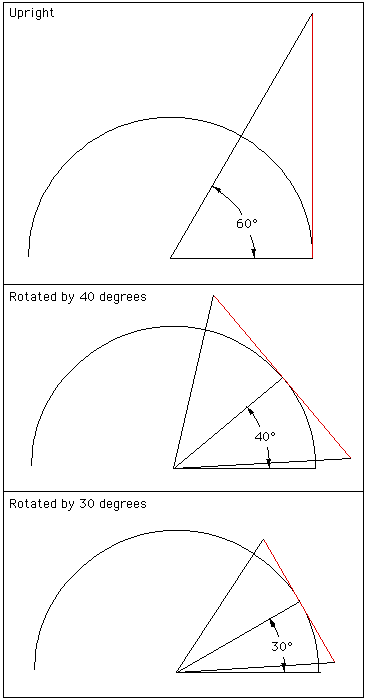
Test pattern The image below was used as the initial test pattern, the results for each of the panel positions is shown below (click on images for the full size fisheye). As expected there is quite a bit of compression involved so good antialiasing is mandatory, in the cases shown here a 3x3 adaptive antialias was employed. Upright Rotate by 45 degrees Rotate by 30 degrees Another example - A slide from a KeyNote presentation Slides for spherical mirror full dome projection Slides to fisheye Written by Paul Bourke An alternative, April 2006 This utility maps rectangular images into a fisheye. The rectangular image is placed on a plane that is centered on the north pole of the fisheye (center). It can be scaled by moving the plane closer or further away using the -d option. It is positioned on the fisheye by panning and/or tilting the plane. The plane is always tangential to the sphere, one of many possible geometries. The generated image contains an alpha channel to assist with compositing. Command line usage slide2fish [options] tgafile Options: -a n set antialias level, default: 2 -w n width (and height) of the fisheye image, default: 1024 -s n distance away of the plane, default: 1 unit -x n tilt plane towards rim, default: 0 -z n rotate plane about north pole, default: 0 -d debug mode Example Input image Default mapping, centered on fisheye. Tilted down 40 degrees. Panned by 90 degrees. Tilted by 45 degrees, panned by 90 degrees Panned by -90 degrees, moved further away (scaled) Mapping images into fisheye space so they appear to be on an upright cylinder in a planetarium Written by Paul Bourke April 2007 Aim is to map rectangular images onto a fisheye image such that when viewed in a planetarium the images appear to be wrapped onto cylindrical sections. 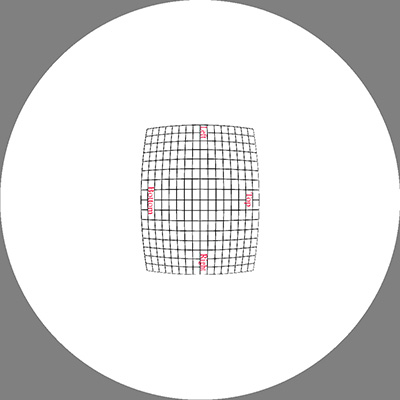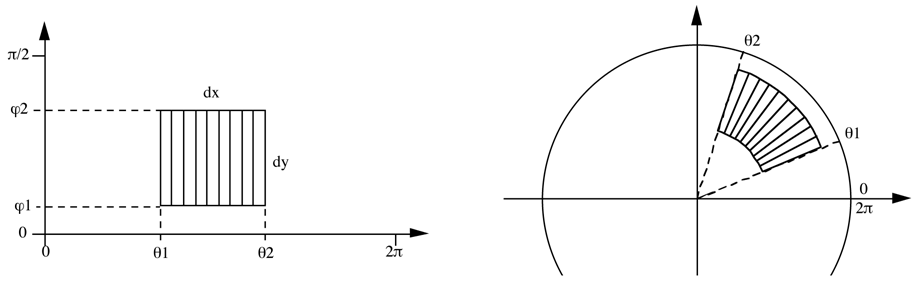Choose the width and position in longitude for the image, this is theta1 and theta2. Also choose the latitude of the base of the image, for example, it might be 0 if the image is to start at the horizon. The image width and height are dx and dy in pixels. We need to determine phi2 such that the image appears in proportion and upright in the dome. 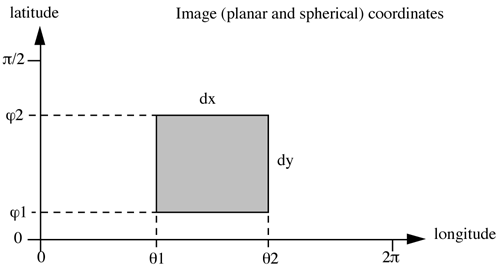Figure 1 The images are imagined to be wrapped around a cylinder. 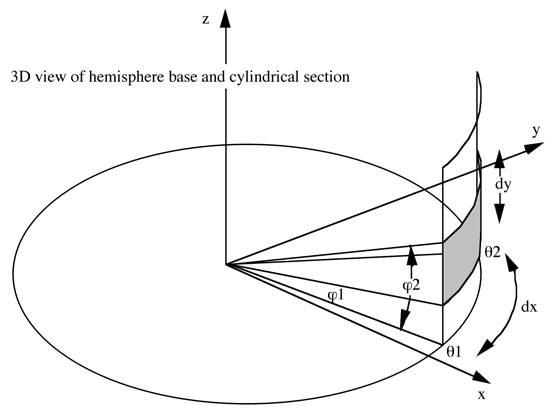Figure 2 Define "r" as the radius of the hemisphere in pixels = dx / (theta2 - theta1) Define dy1 as the height of the base of the image in pixels = r tan(phi1) Then tan(phi2) = (theta2 - theta1)(dy + dx tan(phi1)) / dx For the final fisheye image the goal is to find r1 and r2, once they are known the x,y normalised coordinates of the four corners of the image rectangle in the fisheye can be determined, namely r1(cos(theta1),sin(theta1)), r1(cos(theta2),sin(theta2)), r2(cos(theta2),sin(theta2)), r2(cos(theta1),sin(theta1)) Figure 3 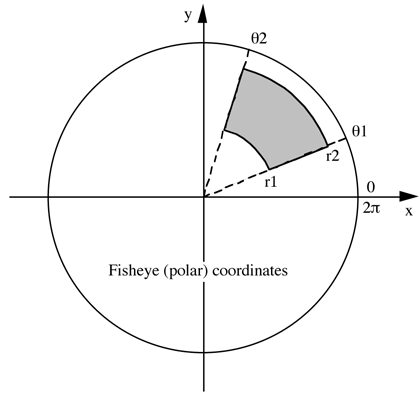r1 = 2 (pi/2 - phi1) / pi r2 = 2 (pi/2 - phi2) / pi Notes phi1 and phi2 are measured in the normal latitude sense in figure 1 and 2, that is, 0 at the horizon. It is traditional to measure angles in fisheye space from the pole (z axis) rather than from the horizon. See the equations for r which contain terms pi/2-phi1 and pi/2-phi2. If the image is to start from the horizon (phi1 = 0) then the expression for phi2 is phi2 = atan((theta2-theta1) dy / dx) When drawing the image as a texture using OpenGL say, one needs to compute smaller quads over subsections of the longitude range. PovRay, or any other 3D rendering engine Written by Paul Bourke Update: June 2010 and February 2016 Of course one can also accomplish this using your favourite 3D rendering/animation package as long as it supports fisheye rendering. Simply create the geometry you wish the image to be mapped onto in a 3D scene and render with a fisheye lens on a appropriately aligned camera. As example of this using PovRay is presented here: pov_billboard_4fisheye.zip. 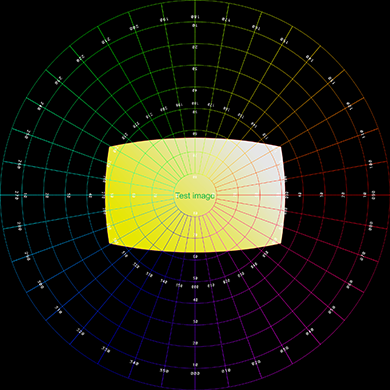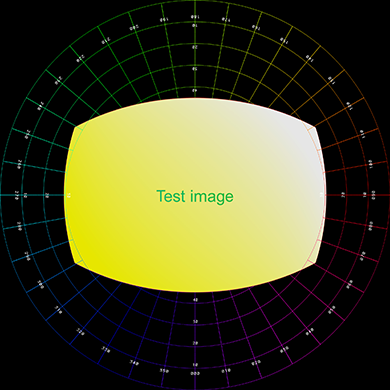This approach makes it easy to animate the texture panels, the same approach is often used for text within a fulldome render. The example provided here takes the image below on the left and renders the image on the right, in a dome this will appear as a vertical pane. 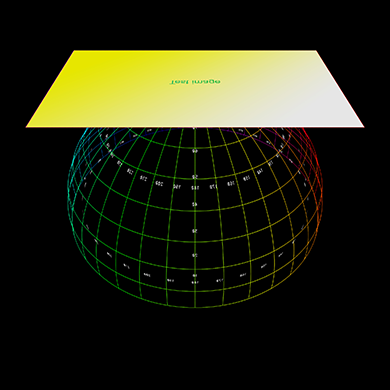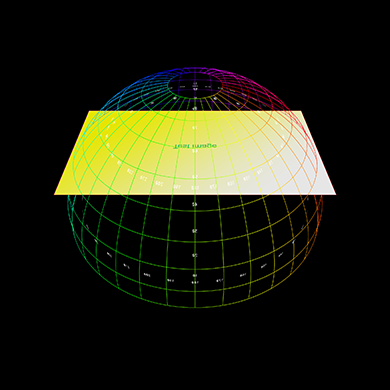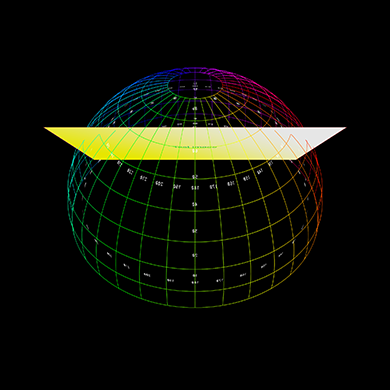Further examples below, the left shows the plane positioned, scaled, angled with respect to the dome, represented as a polar grid. The right shows the result rendered into a fisheye. 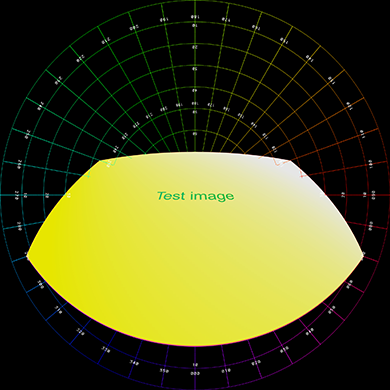Lowered in the dome, brought closer to the viewer. Rotated about a single angle.