Omni-Direction Stereoscopic PanoramasWritten by Paul BourkeMay 2018 Update Dec 2022: Ray origin and view direction for ray tracer Introduction An Omni-Directional Stereoscopic Panorama (ODSP) is a way of creating a 360 degree stereoscopic pair, without the traditional requirement of head tracking if perspective stereo pairs were used. While popularised with the current wave of VR through head mounted displays they have been known for some time [Ref 1]. They provide a stereoscopic experience that is perfect in the center of the observers view but which becomes increasingly incorrect to the left and right of that center. As the observer turns their head the stereoscopic pairs observed remain correct in the center of the view. In practice the error from the center of the view center does not seriously impact the experience, some reasons are:
While the ODSP is designed to be view direction independent, it is not position depended, that still requires head tracking for strict correctness. It should be noted that all stereoscopic displays have perceived depth errors if the viewer is not located in the position for which the stereoscopic pair was generated, for more information see: Spatial errors in stereoscopic displays. The most common applications for ODSP is to create 360 degree stereoscopic movie content when doing so interactively is not possible. For large scale cylindrical displays [Ref 2] it supports multiple participants, each getting an acceptable stereoscopic experience even though they may all be looking in different directions. Note that in this later case the ODSP may be created in real-time or pre-rendered. In addition to computer generated ODSPs, images of real world scenes can be captured by a spinning camera pair. If the step sizes are small enough this results in parallax error free stereoscopic panoramas, something that multiple camera rigs can not achieve. Omni-Directional Stereoscopic Cylindrical Panorama
Stereoscopic cylindrical panoramas can be classified in two ways, the first is destined for head mounted displays, that is, zero parallax is at infinity. The second is designed for a cylindrical display where the zero parallax is at some distance from the observer, typically the radius of the cylinder. The mathematics for the typical reverse pixel lookup is given below. Specifically, given a pixel on the final cylindrical panorama, what is the corresponding camera position (for both left and right eye) and what is the view vector. 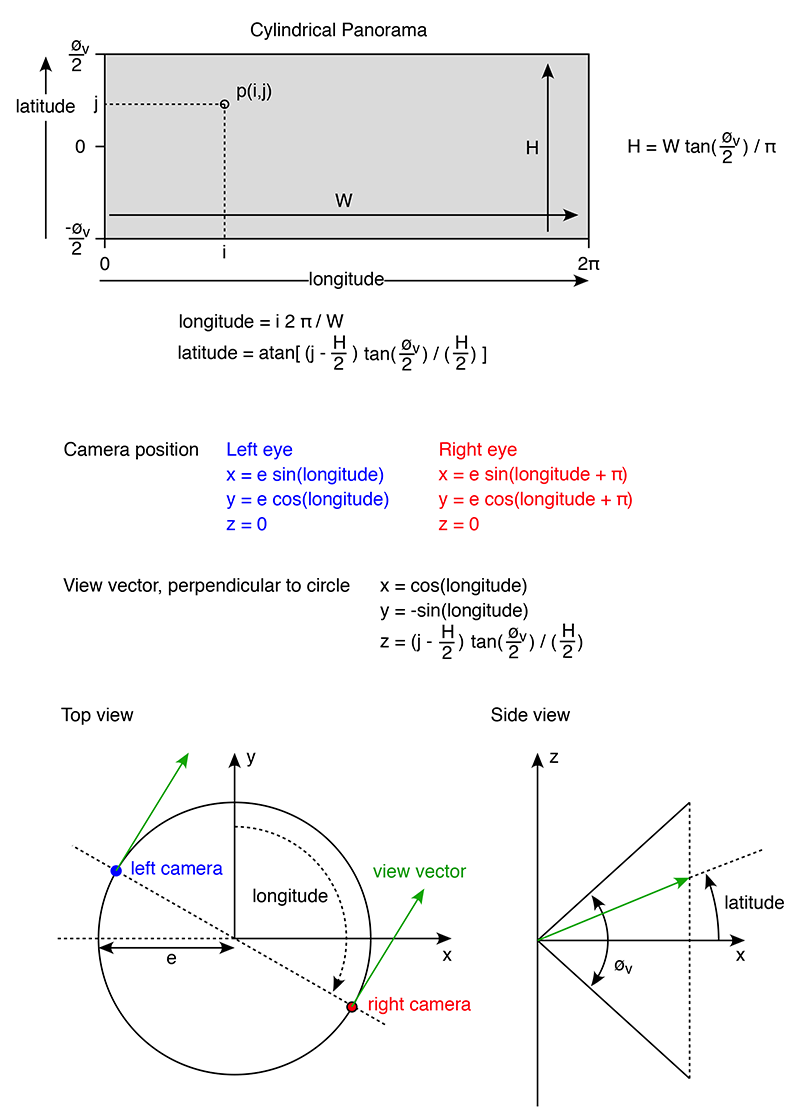
The above assumes the center of the camera rig is located at the origin and lies in the x-y plane, z is the up vector. Variations to this simply involve coordinate system rotations and translations. The interocular separation is 2e. A cylindrical panorama is characterised by the vertical field of view øv. The height H in pixels given a width W is given by the experession shown. For a large scale cylindrical display the vertical field of view would normally match that of the display geometry. For other displays, such as head mounted one chooses a vertical field of view depending on the intended lookup and down extent required, noting that cylindrical panoramas become increasingly inefficient as the vertical field of view increases past 120 degrees. This vertical inefficiency is the same as that experienced with very wide perspective views, a cylindrical panorama has the same vertical relationship as that of a perspective projection. The following movie illustrates the camera positions and view vectors for a selection of points on the cylindrical panorama. 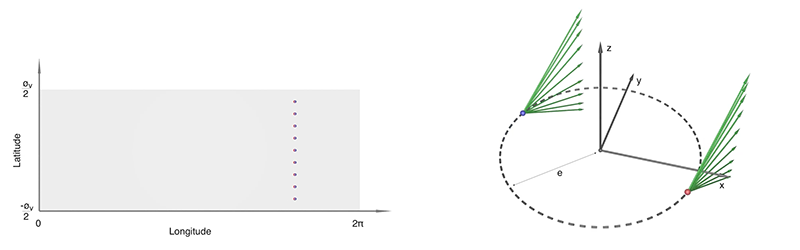
In the case of projected cylindrical displays the option exists to render with the correct zero parallax, typically at the radius of the display. In the authors opinion it is preferable to render as the above (zero parallax at infinity) and control the actual zero parallax in the player. This amounts to simply a rotation of one of the panoramas about the up vector. Omni-Directional Stereoscopic Spherical Panorama
The equivalent equations are given below for a spherical panorama, also known as an equirectangular projection. The same conventions are use as for the above. The main difference is that now the vertical field of view is not limited and extends all the way from -π/2 to π/2 although noting there is a singularity at the these points, the south and north pole. There are a number of possible strategies to deal with the poles, most aim at removing the stereoscopic effect there, for example, by gradually reducing the interocular e to zero. Another option is to simply constrain the camera to not allow views of the poles. In photographically derived images it is customary to place occluding caps at the poles. The height H of the equirectangular given the width W is now simply H = W/2. 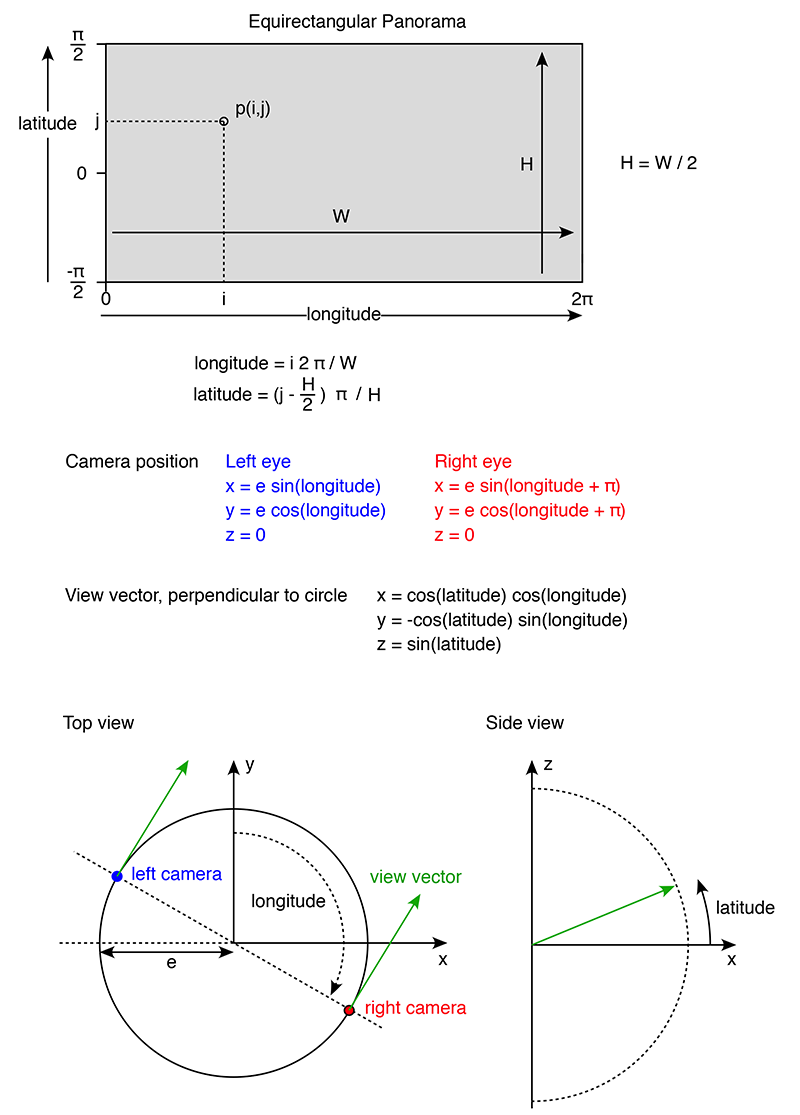
The following movie illustrates the camera positions and view vectors for a selection of points on the spherical panorama (equirectangular projection). 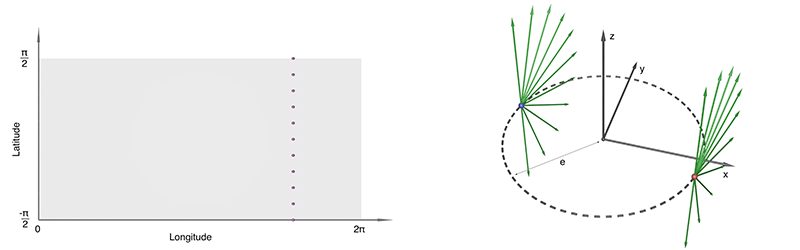
For projection based dome displays such as the iDome or a digital planetarium one also needs control over the zero parallax distance. This dictates how the view direction rays "toe-in" to intersect at the zero parallax distance. Unlike the cylindrical case this is no longer a simple rotation of one panorama with respect to the other. References
1. H. Ishiguro, M. Yamamoto, and S. Tsuji, Omni-Directional Stereo, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 14, No. 2, pp. 257-262, February 1992. 2. McGinity, M., Shaw, J., Kuchelmeister, V., Hardjono, A. & Del Favero, D. (2007) AVIE: a versatile multi-user stereo 360° interactive VR theatre. In Proceedings of the 2007 Workshop on Emerging Displays Technologies: Images and Beyond: the Future of Displays and interaction (San Diego, California, August 4 - 04, 2007). EDT '07, vol. 252. ACM, New York, NY. 3. S. Peleg and M. Ben-Ezra, Stereo Panorama with a Single Camera. Proc. IEEE Conf. Computer Vision and Pattern Recognition, pp. 395-401, June 1999. 4. S. Peleg, M. Ben-Ezra, and Y. Pritch. Omnistereo: Panoramic Stereo Imaging. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 23, No. 3, pp 279-290, March 2001. 5. Bourke, P.D. Synthetic stereoscopic panoramic images. Lecture Notes in Computer Science (LNCS), Springer, ISBM 978-3-540-46304-7, Volume 4270, 2006, pp 147-155 Camera examples
|

