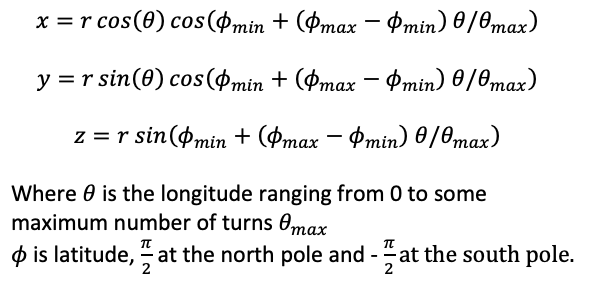Mapping long thin images into higher dimensions

Introduction

The following presents various ways of mapping extremely long thin images, or data, into a more compact form. This is achieved by raising the dimension of the data, embedding the 1D strip onto 2 or 3 dimensional geometry. The example used is a slitscan image recorded on a train from Geelong to Melbourne over the period of 1 hour. The image is approximately 100,000 pixels long by only 2300 pixels high, so an aspect ratio of 44:1. A scaled down version at 30,000 pixels is given below, Geelong on the left and Melbourne on the right one hour later.

Spring

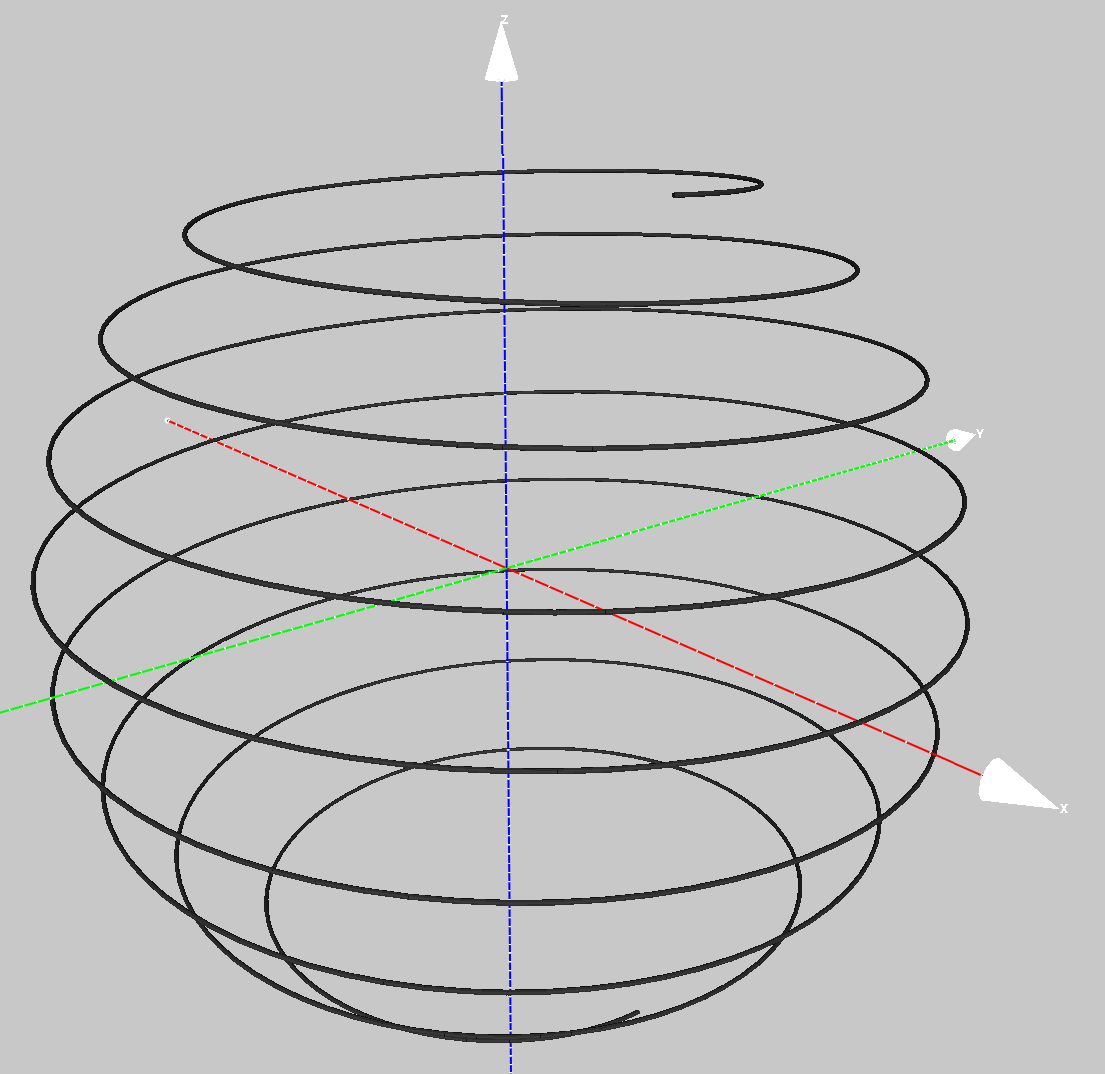
The first approach is to map the image onto a vertical spiral spring surface. This maps the length of the image onto an arbitrary long circumference of the spring. Exploring the image requires a real-time 3D interaction with the textured geometry. The equations for the spring is given below where r is the radius in the x-y plane, theta ranges from 0 to the total winding angle, and d_z determines the spacing between the rings.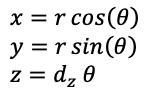

In the following, the total winding angle is 1080 degrees, the radius is 1, and d_z set so the spring lies within a unit cube.

Flat spiral

The second approach is to retain the 2D nature of the image and spiral it on a plane. There are many possible spiral forms one could use. Most suited here is a spiral where the curves are equally separated radially, this is a feature of the Archimedean spiral and described simply by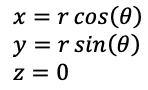

Where r varies linearly between two ranges, the inner smaller radius and the larger outer radius. Theta determines the total angular extent. In the following the radius extends from 1 to 4 and the angle from 0 to 1800 degrees.

Spherical spiral

The last case is to wrap the long strip onto the surface a sphere. One of the benefits of this is that one can then render the result as a static equirectangular image for viewing within VR headsets or online in one of the many social media platforms that support 360 spherical panoramas.

The standard spiral on a sphere describes a ship which travels from one pole to the other pole while keeping a fixed angle with respect to the meridians. This isn't suitable since it results in a compression of the curves at the poles. For the purpose here we need a curve on a sphere where the curves stay equally spaced, the same desirable attribute for the 2D spiral. Such a curve is given in the equations and figure below. In the above example the latitude ranges from -60 to 60 degrees and the longitude from 0 to 2880 degrees.

An example with a larger number of windings.

Notes

• A feature of all the approaches above is that the available length of the curve available for the image mapping only depends on the angle parameter, and not the size of the shape. This is because increasing the radial size also increases the width of the strip.

• A key constraint when choosing the total angle is whether the image strips intersect. For a particular aspect ratio there will be a minimum total angle that avoids overlaping or adjacent strips.

• The examples here are created as textured OBJ models and can thus be opened in a wide range of software and online 3D viewers. An important consideration for image quality is to understand that texture maps for 3D viewers should not be too large, 4096 is safe, 8192 is usually OK but using higher resolution textures is risky. For the examples here the original image strip is split into 20 pieces and the mesh is textured accordingly along its length. Each texture is therefore around 5000 pixels wide. Some examples can be found here:

  3D spring, 2D spiral, 3D sphere.

• An example of a navigable version of the spherical spiral case.