The source code implementing the projections below is only available on request for a small fee. It includes a demo application and an invitation to convert an image of your choice to verify the code does what you seek. For more information please contact the author.

The making of ... and third place in the UWA Friends of the Grounds Photographic Competition, 2011.

Appears on the cover of the UWA Friends of the Grounds Calendar, 2012 Centenary edition and 2013 calendar.

Command line usage string.

Usage: sphere2stereo [options] sphereimage
Options
   -w n n     width and height of the stereographic image, default = 512x512
   -t n       stereographic radius, default = 8
   -a n       antialiasing level, default = 2
   -x n       x axis panning rotate, default = 0
   -y n       y axis panning rotate, default = 0
   -z n       z axis panning rotate, default = 0
   -o s       output file name, name derived from input filename
   -h n       height of nodal point, typically between 0 and 1, default: 1
   -f n       multiplicate fading, default: 1 (none)
   -r         clip to unit circle, default: disabled

The images here are created using stereographic projections, it is one of the many ways of mapping points on a sphere onto a plane. Since a sphere and a plane are topologically different forms, the mapping cannot be performed without some form of distortion. Stereographic projections, also called planisphere projections have been employed by Hipparchus and documented by Ptolemy, it arises as a way of mapping spherical data onto an image plane in a range of fields that include astronomy, cartography, geology, and mathematics.

The first stage is the creation of a spherical projection, otherwise known as a equirectangular projection of a sphere. There are many ways of doing this photographically, they are mostly distinguished from each other by the final image resolution. The simplest is with a 180 degree fisheye lens and SLR camera. Three images are captured each separated by 120 degrees horizontally.

Since these three images capture the entire visual field, 360 degrees horizontally and 180 degrees vertically, they can be stitched and blended together to form a spherical projection, as follows.

It is this image, mapped as a texture onto a sphere, that can be projected onto a plane using a stereographic projection. A stereographic projection involves selecting a focal point (normally along a vertical line through the origin) and a plane which will become the projected image plane. To determine where any point on the sphere maps to on the image plane, a ray is drawn from the focal point through the point in question. Where this ray intersects the image plane is the projected position. In this case the focal point is the north pole of the sphere and the image plane is tangential to the sphere and touches the south pole. This is illustrated below for two points in the image, the top of the building roof and the yacht mast.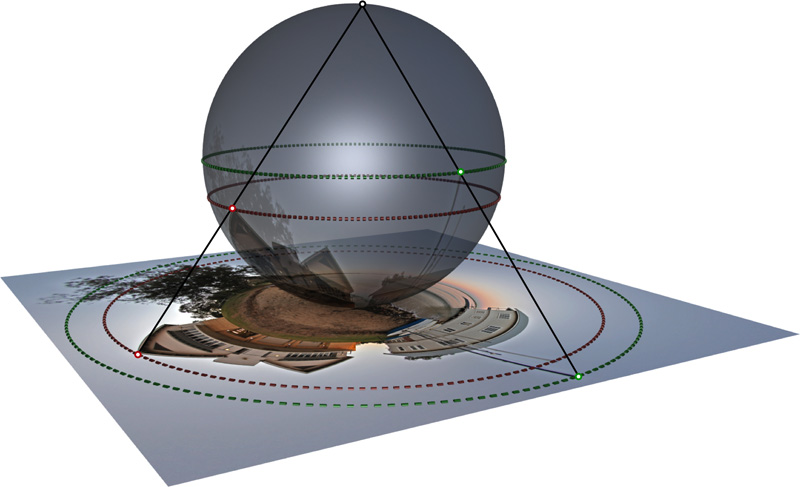

Stereographic projections preserve angles (conformal) but they do not preserve lengths (obvious if one considers what happens to points towards the north pole) and it therefore follows that it does not preserve area (isometric). The projection is smooth (no discontinuities), at least for points on the sphere between the focal point and the image plane.

Fisheye images are generally created with a 180 degree field of view, that is, the view with a hemisphere as the projection surface. However, the mathematics that describes a fisheye can extend the angles to 360 (actually even further than that but it results in a space replication). The images below are the result of creating a fisheye projection with the camera looking straight down and the fisheye angle is 360 degrees. The result is strangely compelling, they can appear to be a planet on which extreme structures have been built.

Corresponding raw spherical panoramic image

The images here are captured using a 185 degree fisheye lens on a SLR camera. Three images are captured each with the camera/lens rotated 120 degrees horizontally with respect to the other images. These three fisheye images are stitched together to form a 360 degree by 180 degree spherical projection. This image (also linked to for each example) is then resampled to a 360 degree fisheye using locally developed software, namely sphere2fish.

Corresponding raw spherical panoramic image

There are some extreme distortions occurring, for example, the entire rim of the image is in fact a single point corresponding to the north pole.

Corresponding raw spherical panoramic image

The images here are all from the University of Western Australia. The first is the South side of Hackett hall, the second the North side, the last is the Reid Library.

Stereographic projection (Little Planet)

Another technique that gives similar results, but perhaps more striking, uses stereographic projections. Corresponding stereographic projections given below.

The utility that creates these converts spherical projections into stereographic projections. The main variable is the size of the projection radius (-t).

Usage: sphere2stereo [options] sphereimage
Options
   -w n n     width and height of the stereographic image, default = 512x512
   -t n       stereographic radius, default = 4
   -a n       antialiasing level, default = 2
   -z n       z axis panning rotate, default = 0 (Applied first)
   -y n       y axis panning rotate, default = 0
   -x n       x axis panning rotate, default = 0
   -o s       output file name, name derived from input filename
   -h n       height of nodal point, typically between 0 and 1, default: 1
   -f n       multiplicate fading, default: 1 (none)

A stereographic projection can be visualised as a sphere, a line is drawn from the north pole to each point on the sphere surface, for example P₁ and P₂. Where that line intersects a plane that touches the south pole, is the position of the point on the stereographic projection plane, for example P'₁ and P'₂.

Rotomahana, New Zealand

Stereographic projections from slitscan equirectangulars

Slit scans can also be applied to 360 video, namely equirectangular images. It can be applied both horizontally (rows) and vertically (columns). The following spans 1 hour, 6pm on the left edge and 7pm at the right edge, it still wraps like a normal equirectangular image except of course for the brightness change.

These in turn can be remapped to stereographic images.

Stereographic projections to smoothed equirectangulars

In the following this is a 5 minute average applied to the equirectangular footage from a 360 video camera.

And turned into stereographic projections.