Interpolation methodsWritten by Paul BourkeDecember 1999
Discussed here are a number of interpolation methods, this is by no means an exhaustive list but the methods shown tend to be those in common use in computer graphics. The main attributes is that they are easy to compute and are stable. Interpolation as used here is different to "smoothing", the techniques discussed here have the characteristic that the estimated curve passes through all the given points. The idea is that the points are in some sense correct and lie on an underlying but unknown curve, the problem is to be able to estimate the values of the curve at any position between the known points.
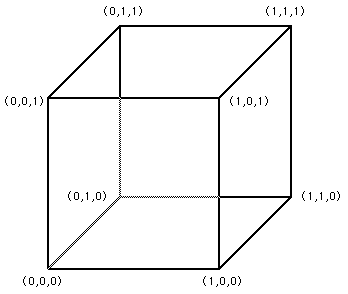
Trilinear InterpolationWritten by Paul BourkeJuly 1997 Trilinear interpolation is the name given to the process of linearly interpolating points within a box (3D) given values at the vertices of the box. Perhaps its most common application is interpolating within cells of a volumetric dataset.
The value at position (x,y,z) within the cube will be denoted Vxyz and is given by
In general the box will not be of unit size nor will it be aligned at the origin. Simple translation and scaling (possibly of each axis independently) can be used to transform into and then out of this simplified situation.
Linear RegressionWritten by Paul BourkeOctober 1998 Linear regression is a method to best fit a linear equation (straight line) of the form y(x) = a + b x to a collection of N points (xi,yi). Where b is the slope and a the intercept on the y axis. The result will be stated below without derivation, that requires minimisation of the sum of the squared distance from the data points and the proposed line. This function is minimised by calculating the derivative with respect to a and b and setting these to zero. For a more complete derivation see the "Numerical Recipes in C". The solution is clearer if we define the following
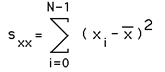
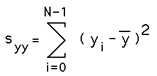
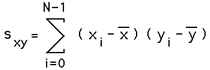 Then
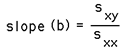 and
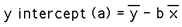 And finally the regression coefficient is
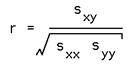 This is 0 if there is no linear trend, 1 for perfect linear fit. Note
ExampleThe following example shows the points and the best fit line as determined using the techniques discussed here.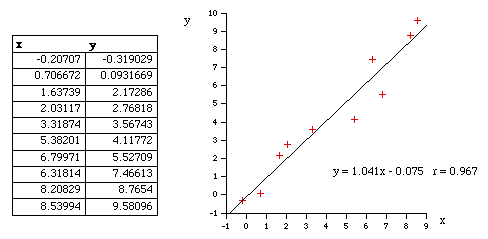
SourceClinregress.c
C++ contributed by Charles Brown
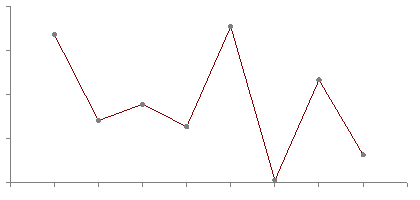
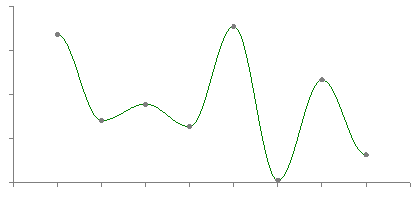
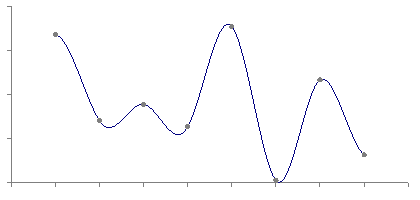
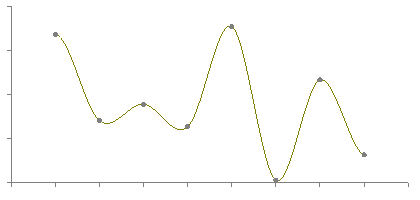
Curve Fit Through Arbitrary PointsWritten by Paul BourkeAugust 1991 The following introduces a method of immediately deriving a polynomial that passes through an arbitrary number of points. That is, find a polynomial f(x) that passes through the N points The key to this solution is that we want an exact fit at the points given and we don't care what happens in between those points. The general solution is 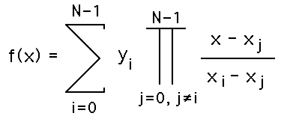
To see how this works, consider the product term. When x = xi the product term has the same denominator and numerator and thus equals 1 and therefore contributes yi to the sum. All other terms in the summation contribute 0 since there exists a (xj - xj) in the numerator. Thanks to Simon Stegmaier for pointing out that this is known as a Lagrange Polynomial. For a numerical example consider the polynomial that passes through the following points
The function using the above formula is
f(x) = 2 * (x-1) * (x-3) * (x-4) * (x-6) / [ (0-1) * (0-3) * (0-4) * (0-6) ]
+ 1 * (x-0) * (x-3) * (x-4) * (x-6) / [ (1-0) * (1-3) * (1-4) * (1-6) ]
+ 3 * (x-0) * (x-1) * (x-4) * (x-6) / [ (3-0) * (3-1) * (3-4) * (3-6) ]
+ 0 * (x-0) * (x-1) * (x-3) * (x-6) / [ (4-0) * (4-1) * (4-3) * (4-6) ]
+ 5 * (x-0) * (x-1) * (x-3) * (x-4) / [ (6-0) * (6-1) * (6-3) * (6-4) ]
f(x) = (x-1) * (x-3) * (x-4) * (x-6) / 36
- (x-0) * (x-3) * (x-4) * (x-6) / 30
+ (x-0) * (x-1) * (x-4) * (x-6) / 6
+ (x-0) * (x-1) * (x-3) * (x-4) / 36
f(x) = 17*x4/90 - 181*x3/90 + 563*x2/90 - 163*x/30 + 2
By substituting the values of x for the points the function must pass through (x=0,1,3,4,6) it is easy to see that the expression above achieves the result, namely y=2,1,3,0,5 respectively. What happens at other points?
All bets are off regarding the behaviour between the fixed points. The polynomial is of degree N and could violently fly off anywhere. The continuous curve for the numerical example above is shown below. 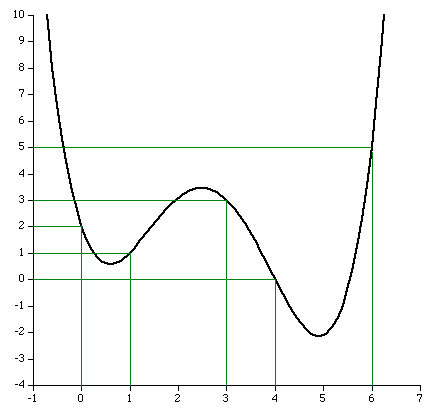 A competition in the Mathematics news groups in October 1998 From: "John Santos" <santos_john@hotmail.com> Newsgroups: alt.sci.math.probability,alt.tv.mathnet,aus.mathematics Subject: $100.00 prize for the solution Date: Tue, 15 Sep 1998 20:56:50 -0700 X-Newsreader: Microsoft Outlook Express 4.72.3110.1 X-MimeOLE: Produced By Microsoft MimeOLE V4.72.3110.3 NNTP-Posting-Host: 209.239.197.111 X-NNTP-Posting-Host: 209.239.197.111 Message-ID: <35ff36d1.0@blushng.jps.net> X-NNTP-Posting-Host: 209.63.114.134 Hi everyone, My name is John Santos and I am willing to pay anyone $100.00 for the first person to solve this problem. I am providing some hints. This works as follows: you will see nine digits - the tenth digit or letter is the answer. What I need is the formula or mathematical equation to get there... Number Answer --------------------------- 749736637 1 713491024 8 523342792 D 749236871 P 727310078 E 746261832 4 733237527 L 743510589 9 715240338 K 722592910 1 739627071 R The first one with the answer and emails it to me wins the $100.00 Email address: santos_john@hotmail.com Good Luck !!!! They refused to pay up for this solution !!!!
The following is the solution to the posted problem, although it probably
doesn't offer the insight you are seeking, it certainly falls within the
scope of competition. To illustrate my solution I will use the following
symbols instead of the numbers you used simply to save space. For your
second column with letters and numbers use their ASCII values instead,
this has no loss of generality as it is a simple 1 to 1 mapping.
x1 y1
x2 y2
x3 y3
x4 y4
etc
The following is a general method of making a function that passes
through any pair of values (xi,yi).
y1 (x-x2) (x-x3) (x-x4)
f(x) = ---------------------------
(x1-x2) (x1-x3) (x1-x4)
y2 (x-x1) (x-x3) (x-x4)
+ ---------------------------
(x2-x1) (x2-x3) (x2-x4)
y3 (x-x1) (x-x2) (x-x4)
+ ---------------------------
(x3-x1) (x3-x2) (x3-x4)
y4 (x-x1) (x-x2) (x-x3)
+ ---------------------------
(x4-x1) (x4-x2) (x4-x3)
etc etc. As you can see, at x=x1 all the terms disappear except the
first which equals y1, at x=x2 all the terms disappear except the
second which equals y2, etc etc.
X Y
Number Answer ASCII
---------------------------------------
749736637 1 49
713491024 8 56
523342792 D 68
749236871 P 80
727310078 E 69
746261832 4 52
733237527 L 76
743510589 9 57
715240338 K 75
722592910 1 49
739627071 R 82
The "lovely" expression in this case isf(x) = + 49 ((x - 713491024) / 36245613) ((x - 523342792) / 226393845) ((x - 749236871) / 499766) ((x - 727310078) / 22426559) ((x - 746261832) / 3474805) ((x - 733237527) / 16499110) ((x - 743510589) / 6226048) ((x - 715240338) / 34496299) ((x - 722592910) / 27143727) ((x - 739627071) / 10109566) + 56 ((x - 749736637) / -36245613) ((x - 523342792) / 190148232) ((x - 749236871) / -35745847) ((x - 727310078) / -13819054) ((x - 746261832) / -32770808) ((x - 733237527) / -19746503) ((x - 743510589) / -30019565) ((x - 715240338) / -1749314) ((x - 722592910) / -9101886) ((x - 739627071) / -26136047) + 68 ((x - 749736637) / -226393845) ((x - 713491024) / -190148232) ((x - 749236871) / -225894079) ((x - 727310078) / -203967286) ((x - 746261832) / -222919040) ((x - 733237527) / -209894735) ((x - 743510589) / -220167797) ((x - 715240338) / -191897546) ((x - 722592910) / -199250118) ((x - 739627071) / -216284279) + 80 ((x - 749736637) / -499766) ((x - 713491024) / 35745847) ((x - 523342792) / 225894079) ((x - 727310078) / 21926793) ((x - 746261832) / 2975039) ((x - 733237527) / 15999344) ((x - 743510589) / 5726282) ((x - 715240338) / 33996533) ((x - 722592910) / 26643961) ((x - 739627071) / 9609800) + 69 ((x - 749736637) / -22426559) ((x - 713491024) / 13819054) ((x - 523342792) / 203967286) ((x - 749236871) / -21926793) ((x - 746261832) / -18951754) ((x - 733237527) / -5927449) ((x - 743510589) / -16200511) ((x - 715240338) / 12069740) ((x - 722592910) / 4717168) ((x - 739627071) / -12316993) + 52 ((x - 749736637) / -3474805) ((x - 713491024) / 32770808) ((x - 523342792) / 222919040) ((x - 749236871) / -2975039) ((x - 727310078) / 18951754) ((x - 733237527) / 13024305) ((x - 743510589) / 2751243) ((x - 715240338) / 31021494) ((x - 722592910) / 23668922) ((x - 739627071) / 6634761) + 76 ((x - 749736637) / -16499110) ((x - 713491024) / 19746503) ((x - 523342792) / 209894735) ((x - 749236871) / -15999344) ((x - 727310078) / 5927449) ((x - 746261832) / -13024305) ((x - 743510589) / -10273062) ((x - 715240338) / 17997189) ((x - 722592910) / 10644617) ((x - 739627071) / -6389544) + 57 ((x - 749736637) / -6226048) ((x - 713491024) / 30019565) ((x - 523342792) / 220167797) ((x - 749236871) / -5726282) ((x - 727310078) / 16200511) ((x - 746261832) / -2751243) ((x - 733237527) / 10273062) ((x - 715240338) / 28270251) ((x - 722592910) / 20917679) ((x - 739627071) / 3883518) + 75 ((x - 749736637) / -34496299) ((x - 713491024) / 1749314) ((x - 523342792) / 191897546) ((x - 749236871) / -33996533) ((x - 727310078) / -12069740) ((x - 746261832) / -31021494) ((x - 733237527) / -17997189) ((x - 743510589) / -28270251) ((x - 722592910) / -7352572) ((x - 739627071) / -24386733) + 49 ((x - 749736637) / -27143727) ((x - 713491024) / 9101886) ((x - 523342792) / 199250118) ((x - 749236871) / -26643961) ((x - 727310078) / -4717168) ((x - 746261832) / -23668922) ((x - 733237527) / -10644617) ((x - 743510589) / -20917679) ((x - 715240338) / 7352572) ((x - 739627071) / -17034161) + 82 ((x - 749736637) / -10109566) ((x - 713491024) / 26136047) ((x - 523342792) / 216284279) ((x - 749236871) / -9609800) ((x - 727310078) / 12316993) ((x - 746261832) / -6634761) ((x - 733237527) / 6389544) ((x - 743510589) / -3883518) ((x - 715240338) / 24386733) ((x - 722592910) / 17034161) f( 749736637) = 49 (1) f( 713491024) = 56 (8) f( 523342792) = 68 (D) f( 749236871) = 80 (P) f( 727310078) = 69 (E) f( 746261832) = 52 (4) f( 733237527) = 76 (L) f( 743510589) = 57 (9) f( 715240338) = 75 (K) f( 722592910) = 49 (1) f( 739627071) = 82 (R) Nearest neighbour weighted interpolationWritten by Paul BourkeApril 1998 The following describes perhaps the simplest method of "smoothly" approximating height values on a surface given a collection of randomly distributed samples. It is often used to derive estimates of the surface height at the vertices of a regular grid from irregularly spaced samples. While the example given here is based on determining the height of a surface (x,y), the same general technique can be used in higher dimensions. For example, estimating the density with a volume (x,y,z) given irregular density measurements. Consider N height samples, that is, we have N triples (xi, yi,zi). We want to estimate the height z given a position on the plane (x,y). The general form of the so called "nearest neighbour weighted interpolation" also sometimes called the "inverse distance method" for estimating z is given by the following. 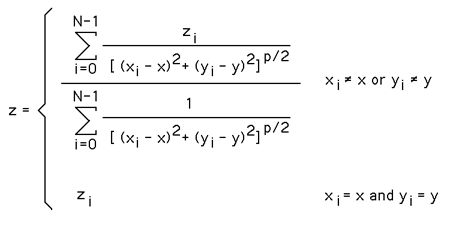 where p generally determines relative importance of distant samples. Note the denominator above gives a measure of how close the point being estimated is from the samples. Naturally if a sample is close then it has a greater influence on the estimate than if the sample is distant.
Colour and Normal InterpolationAs it applies to triangles and quadrilaterals in the rendering of 3D surfacesWritten by Paul BourkeSeptember 2002
It is frequently desirable to estimate the colour or normal at a point in the interior of a 3 or 4 vertex planar polygon given only the colour and normal at each of the vertices. The most common application of this is smooth rendering of surfaces approximated by a finite number of triangular facets or quadrilaterals. Without colour and/or normal interpolation each planar piece of the surface has the same colour and normal, this results in a visible discontinuity between adjacent faces. The following illustrates a part of a sphere made up of quadrilaterals and rendered using a single normal applied to the whole face or 4 normals at each vertex interpolated across the face.
The approach most commonly used by 3D rendering packages, both real-time such as OpenGL and more CPU intensive algorithms such as raytracing, is called Phong normal interpolation. A often used efficient implementation is called barycentric interpolation. The idea is the same for both colour and normal interpolation, a line is extended from the point in question to two edges of the polygon. The estimate of the colour or normal at those points is made by linear interpolation between the values at the vertices of the edge. The estimate at the point in question is linearly interpolated from the estimates at the ends of the extended line. This is illustrated in the sequence below, while this is for normals the method is identical for colours which are after all generally a (r,g,b) triple instead of a (x,y,z) triple. In (A) the point P is where the colour or normal is to be estimated, a line is extended (in any direction but shown as horizontal in this diagram) until it intersects two edges. In (B) the normals at the intersection points of the extended line are shown in red, they are calculated by linear interpolation. In (C) the two normals in (B) are linearly interpolated to give the estimate of the normal at point P. 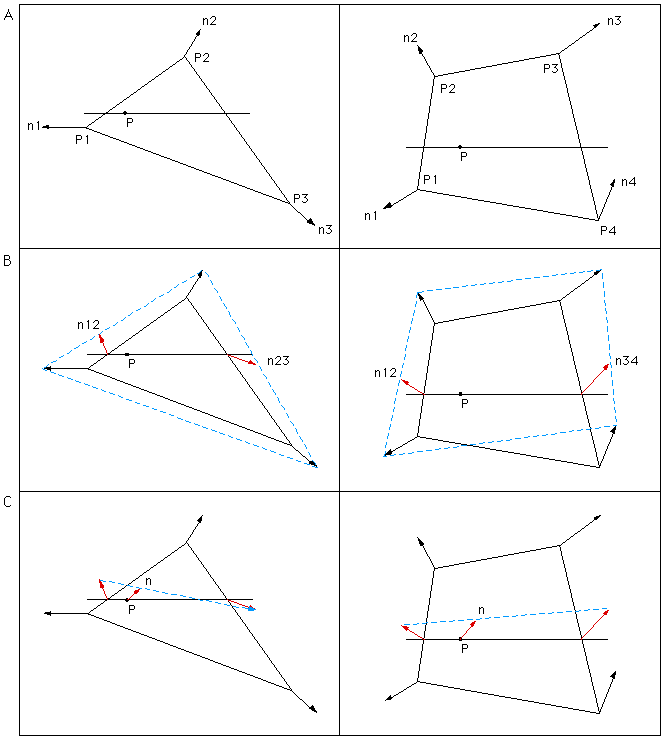
Note
|