Bézier Surface (in 3D)Written by Paul BourkeDecember 1996 Contribution by Prashanth Udupa on Bezier Surfaces in VTK Designer 2: Bezier_VTKD2.pdf
The Bézier surface is formed as the Cartesian product of the blending functions of two orthogonal Bézier curves. 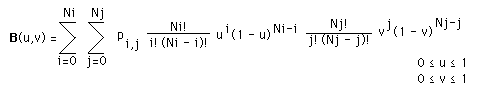
Where Pi,j is the i,jth control point. There are Ni+1 and Nj+1 control points in the i and j directions respectively. The corresponding properties of the Bézier curve apply to the Bézier surface.
Along the edges of the grid patch the Bézier surface matches that of a Bézier curve through the control points along that edge. 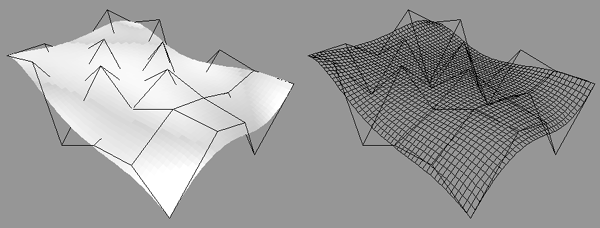
Closed surfaces can be formed by setting the last control point equal to the first. If the tangents also match between the first two and last two control points then the closed surface will have first order continuity. 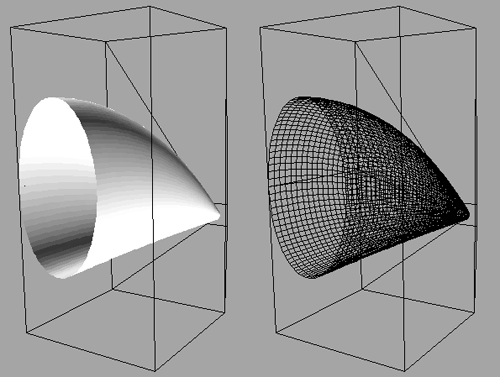 While a cylinder/cone can be formed from a Bézier surface, it is not possible to form a sphere. C Source Example The following source code generates the surface shown in the first example above. It is provided for illustration only, the headers and prototype files are not given.
#define NI 5
#define NJ 4
XYZ inp[NI+1][NJ+1];
#define RESOLUTIONI 10*NI
#define RESOLUTIONJ 10*NJ
XYZ outp[RESOLUTIONI][RESOLUTIONJ];
int main(argc,argv)
int argc;
char **argv;
{
int i,j,ki,kj;
double mui,muj,bi,bj;
/* Create a random surface */
srandom(1111);
for (i=0;i<=NI;i++) {
for (j=0;j<=NJ;j++) {
inp[i][j].x = i;
inp[i][j].y = j;
inp[i][j].z = (random() % 10000) / 5000.0 - 1;
}
}
for (i=0;i<RESOLUTIONI;i++) {
mui = i / (double)(RESOLUTIONI-1);
for (j=0;j<RESOLUTIONJ;j++) {
muj = j / (double)(RESOLUTIONJ-1);
outp[i][j].x = 0;
outp[i][j].y = 0;
outp[i][j].z = 0;
for (ki=0;ki<=NI;ki++) {
bi = BezierBlend(ki,mui,NI);
for (kj=0;kj<=NJ;kj++) {
bj = BezierBlend(kj,muj,NJ);
outp[i][j].x += (inp[ki][kj].x * bi * bj);
outp[i][j].y += (inp[ki][kj].y * bi * bj);
outp[i][j].z += (inp[ki][kj].z * bi * bj);
}
}
}
}
printf("LIST\n");
/* Display the surface, in this case in OOGL format for GeomView */
printf("{ = CQUAD\n");
for (i=0;i<RESOLUTIONI-1;i++) {
for (j=0;j<RESOLUTIONJ-1;j++) {
printf("%g %g %g 1 1 1 1\n",
outp[i][j].x, outp[i][j].y, outp[i][j].z);
printf("%g %g %g 1 1 1 1\n",
outp[i][j+1].x, outp[i][j+1].y, outp[i][j+1].z);
printf("%g %g %g 1 1 1 1\n",
outp[i+1][j+1].x,outp[i+1][j+1].y,outp[i+1][j+1].z);
printf("%g %g %g 1 1 1 1\n",
outp[i+1][j].x, outp[i+1][j].y, outp[i+1][j].z);
}
}
printf("}\n");
/* Control point polygon */
for (i=0;i<NI;i++) {
for (j=0;j<NJ;j++) {
printf("{ = SKEL 4 1 \n");
printf("%g %g %g \n",inp[i][j].x,inp[i][j].y,inp[i][j].z);
printf("%g %g %g \n",inp[i][j+1].x,inp[i][j+1].y,inp[i][j+1].z);
printf("%g %g %g \n",inp[i+1][j+1].x,inp[i+1][j+1].y,inp[i+1][j+1].z);
printf("%g %g %g \n",inp[i+1][j].x,inp[i+1][j].y,inp[i+1][j].z);
printf("5 0 1 2 3 0\n");
printf("}\n");
}
}
}
Bézier Blending Function
This function computes the blending function as used in the Bézier surface code above. It is written for clarity, not efficiency. Normally, if the number of control points is constant, the blending function would be calculated once for each desired value of mu.
double BezierBlend(k,mu,n)
int k;
double mu;
int n;
{
int nn,kn,nkn;
double blend=1;
nn = n;
kn = k;
nkn = n - k;
while (nn >= 1) {
blend *= nn;
nn--;
if (kn > 1) {
blend /= (double)kn;
kn--;
}
if (nkn > 1) {
blend /= (double)nkn;
nkn--;
}
}
if (k > 0)
blend *= pow(mu,(double)k);
if (n-k > 0)
blend *= pow(1-mu,(double)(n-k));
return(blend);
}
Bézier curvesWritten by Paul BourkeOriginal: April 1989, Updated: December 1996
The following describes the mathematics for the so called Bézier curve. It is attributed and named after a French engineer, Pierre Bézier, who used them for the body design of the Renault car in the 1970's. They have since obtained dominance in the typesetting industry and in particular with the Adobe Postscript and font products. Consider N+1 control points pk (k=0 to N) in 3 space. The Bézier parametric curve function is of the form 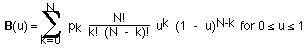
B(u) is a continuous function in 3 space defining the curve with N discrete control points Pk. u=0 at the first control point (k=0) and u=1 at the last control point (k=N). 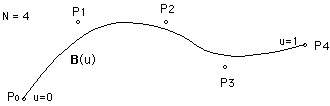 Notes:
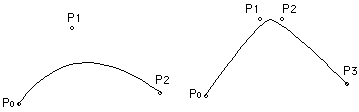
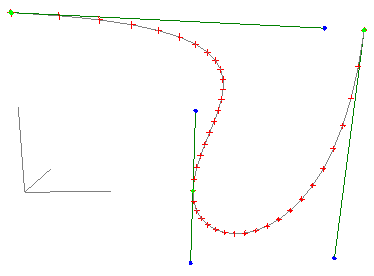
Bézier curves have wide applications because they are easy to compute and very stable. There are similar formulations which are also called Bézier curves which behave differently, in particular it is possible to create a similar curve except that it passes through the control points. See also Spline curves. ExamplesThe pink lines show the control point polygon, the grey lines the Bézier curve.
/*
Three control point Bezier interpolation
mu ranges from 0 to 1, start to end of the curve
*/
XYZ Bezier3(XYZ p1,XYZ p2,XYZ p3,double mu)
{
double mum1,mum12,mu2;
XYZ p;
mu2 = mu * mu;
mum1 = 1 - mu;
mum12 = mum1 * mum1;
p.x = p1.x * mum12 + 2 * p2.x * mum1 * mu + p3.x * mu2;
p.y = p1.y * mum12 + 2 * p2.y * mum1 * mu + p3.y * mu2;
p.z = p1.z * mum12 + 2 * p2.z * mum1 * mu + p3.z * mu2;
return(p);
}
/*
Four control point Bezier interpolation
mu ranges from 0 to 1, start to end of curve
*/
XYZ Bezier4(XYZ p1,XYZ p2,XYZ p3,XYZ p4,double mu)
{
double mum1,mum13,mu3;
XYZ p;
mum1 = 1 - mu;
mum13 = mum1 * mum1 * mum1;
mu3 = mu * mu * mu;
p.x = mum13*p1.x + 3*mu*mum1*mum1*p2.x + 3*mu*mu*mum1*p3.x + mu3*p4.x;
p.y = mum13*p1.y + 3*mu*mum1*mum1*p2.y + 3*mu*mu*mum1*p3.y + mu3*p4.y;
p.z = mum13*p1.z + 3*mu*mum1*mum1*p2.z + 3*mu*mu*mum1*p3.z + mu3*p4.z;
return(p);
}
/*
General Bezier curve
Number of control points is n+1
0 <= mu < 1 IMPORTANT, the last point is not computed
*/
XYZ Bezier(XYZ *p,int n,double mu)
{
int k,kn,nn,nkn;
double blend,muk,munk;
XYZ b = {0.0,0.0,0.0};
muk = 1;
munk = pow(1-mu,(double)n);
for (k=0;k<=n;k++) {
nn = n;
kn = k;
nkn = n - k;
blend = muk * munk;
muk *= mu;
munk /= (1-mu);
while (nn >= 1) {
blend *= nn;
nn--;
if (kn > 1) {
blend /= (double)kn;
kn--;
}
if (nkn > 1) {
blend /= (double)nkn;
nkn--;
}
}
b.x += p[k].x * blend;
b.y += p[k].y * blend;
b.z += p[k].z * blend;
}
return(b);
}
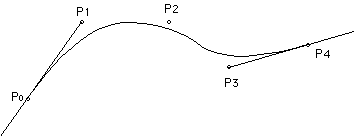
Piecewise Cubic Bézier CurvesWritten by Paul BourkeMarch 2000
Given four points p0, p1, p2, and p3 in 3D space the cubic Bézier curve is defined as where t ranges from 0 (the start of the curve, p0) to 1 (the end of the curve, p3). The vectors a, b, c are given as follows:
b = 3 (p2 - p1) - c a = p3 - p0 - c - b
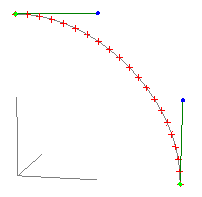
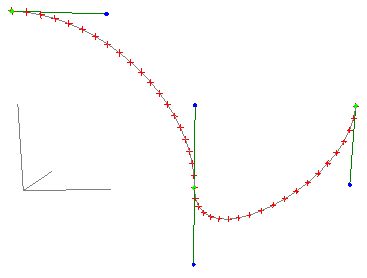
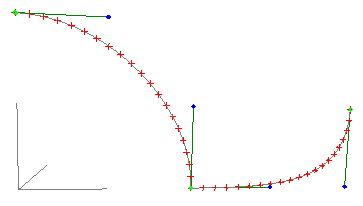
In the following examples the green markers correspond to p0 and p3 of each section. The blue markers correspond to p1 and p2. The grey curve is the Bézier curve sampled 20 times, the samples are shown in red. The coordinates for each vertex is shown on the right.
Example 1
Example 2
Example 3
Example 4
Example 5
Notes
Source code
/*
Piecewise cubic bezier curve as defined by Adobe in Postscript
The two end points are p0 and p3
Their associated control points are p1 and p2
*/
XYZ CubicBezier(XYZ p0,XYZ p1,XYZ p2,XYZ p3,double mu)
{
XYZ a,b,c,p;
c.x = 3 * (p1.x - p0.x);
c.y = 3 * (p1.y - p0.y);
c.z = 3 * (p1.z - p0.z);
b.x = 3 * (p2.x - p1.x) - c.x;
b.y = 3 * (p2.y - p1.y) - c.y;
b.z = 3 * (p2.z - p1.z) - c.z;
a.x = p3.x - p0.x - c.x - b.x;
a.y = p3.y - p0.y - c.y - b.y;
a.z = p3.z - p0.z - c.z - b.z;
p.x = a.x * mu * mu * mu + b.x * mu * mu + c.x * mu + p0.x;
p.y = a.y * mu * mu * mu + b.y * mu * mu + c.y * mu + p0.y;
p.z = a.z * mu * mu * mu + b.z * mu * mu + c.z * mu + p0.z;
return(p);
}
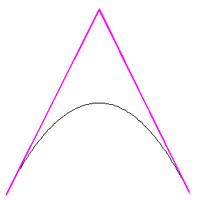
FAQ A common application for these curves in computer graphics is the creation of a smooth flight path that passes through keyframe points in space. The basic issue is how to derive the tangent vectors for each piece of the curve. There are two ways one might achieve this that are illustrated in the drawings below. The first approach is easiest but often lends to unnecessary "swerving", the second method is "smoother". In what follows the keyframes and points p0 to p5, in order to use the Piecewise Cubic Bézier for each section (between points pi and pi+1) one needs to find the tangent vectors shown in red. Note that for continuity between the points the tangent vector at the end of one piece is the negative of the tangent at the start of the next piece. In this first case the tangent vectors are just the differences between subsequent keyframe points. So for example, for the segment between p1 and p2 the four points use for the Bézier would be p1, p2, 2p2-p3, p2. Depending on the length scaling for the tangent vectors, the resulting Bézier curve between points p1 and p3 is shown in blue. 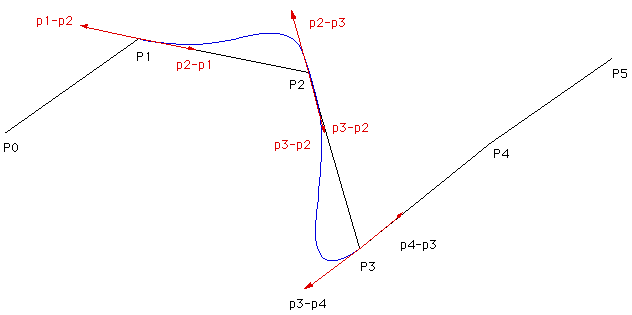
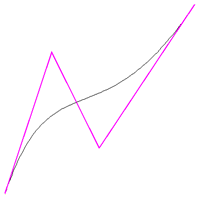
A generally better method is shown below, again one needs to find the red tangent vectors. The exact implementation will be left up to the reader but the approach I've used is to find the cross product between the vectors to each neighbour, that is a vector coming out of the page (or into the page) in the diagram below. The tangent vectors (red) are found by taking the cross product of that with the green normal vectors. The main reason for using this approach is that it overcomes a mirror symmetry problem that occurs if one simple tries to rotate the green normal vectors +- 90 degrees. Note that the case of 3 collinear points needs to be treated as a special case. 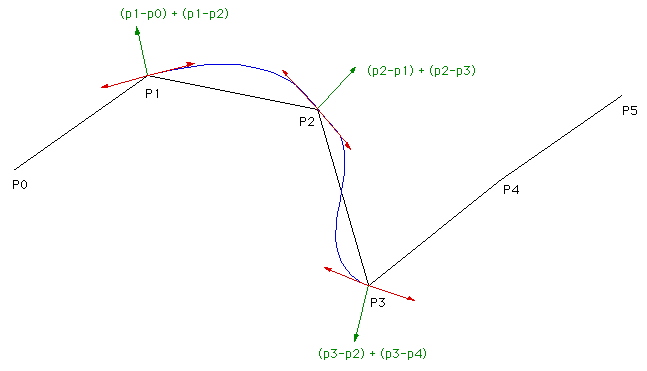
An improvement by Lars Jensen is illustrated below. It uses a normal that bisects the two vectors to the neighbouring points along with way of limiting the tangent lengths. 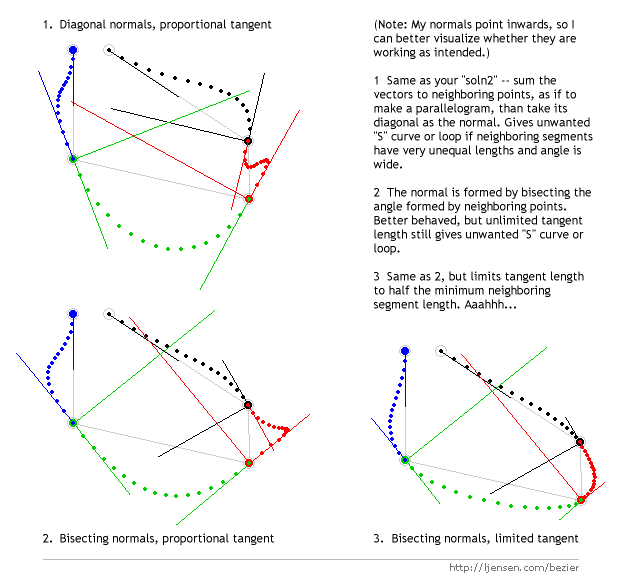 The only remaining comment is how one deals with the first and last point, normally there are some ad hoc approaches that are application specific. |