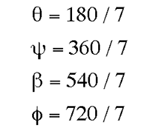Tiling the plane, periodic and aperiodicThe follows are notes on various tilings on the plane.
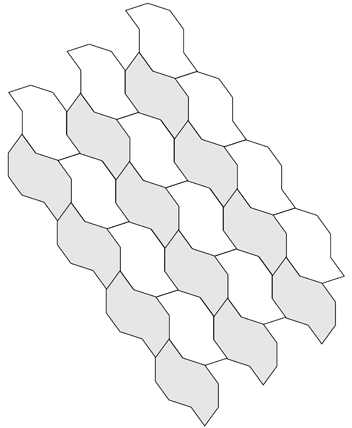
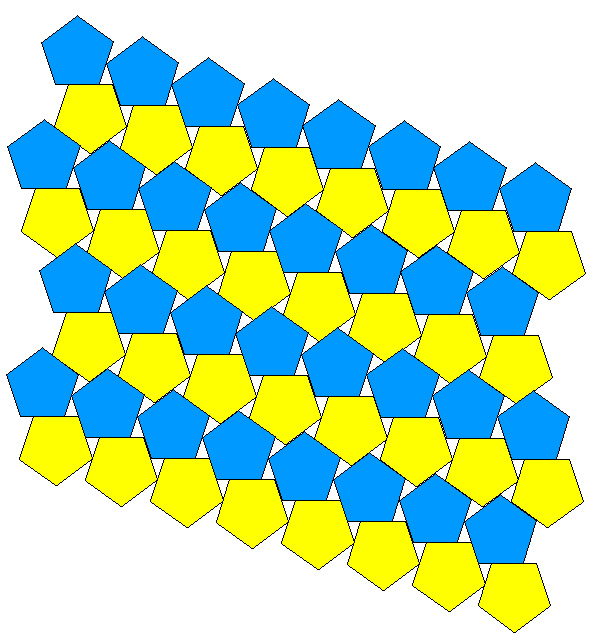
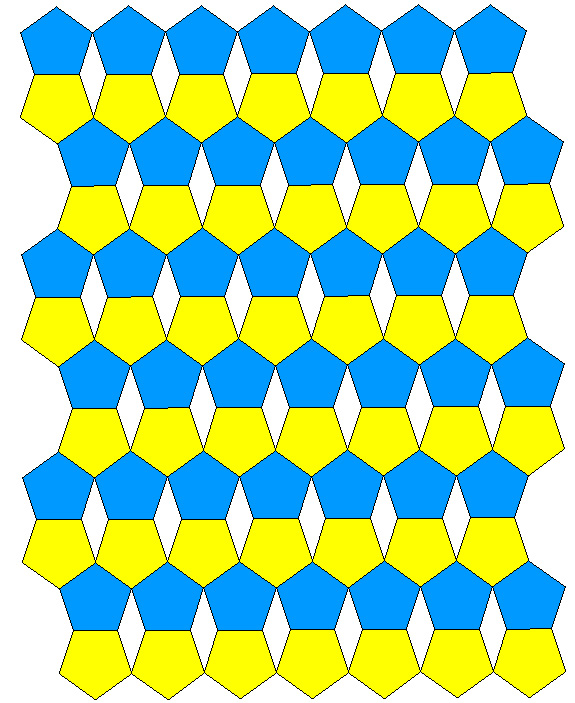
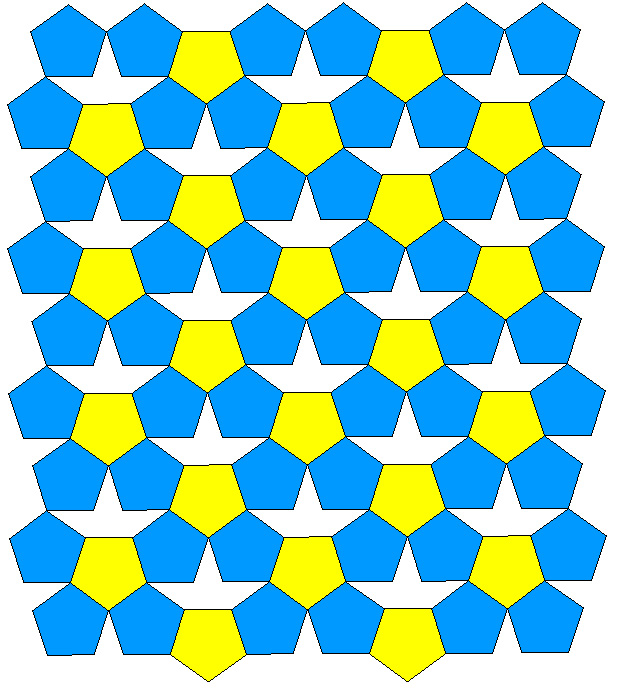
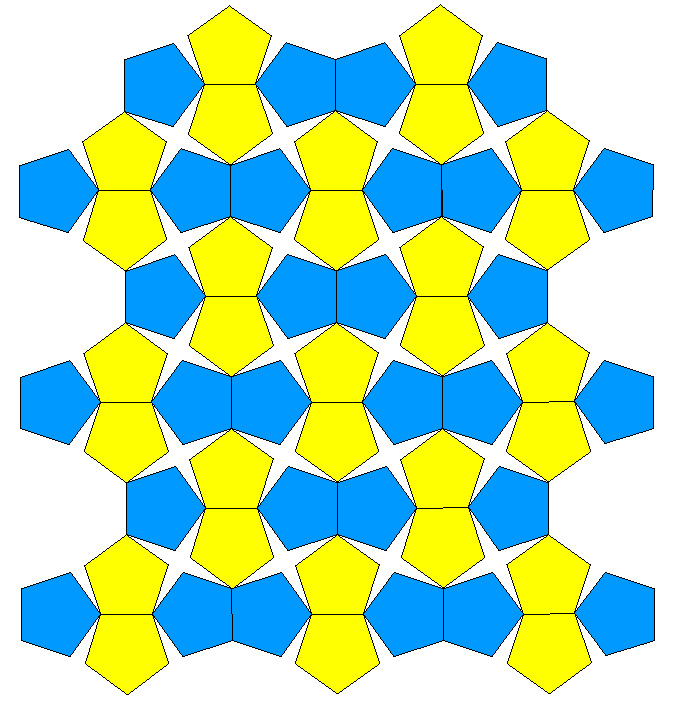
Regular Pentagon tiling examplesWritten by Paul BourkeDecember 2001
Truchet tiles in 2D and 3DWritten by Paul BourkeJune 2006 Named after Sebastien Truchet (1657 - 1729) who studied tiling of squares with a diagonal orientation. 2 DimensionsSingle cell
2x2 tilings
Each unit is randomly rotated by 0 or 90 degrees or flipped vertically or horizontally, there are only two unit states.
5x5 tilings
Larger tiling [POVRay source]


3 DimensionsSingle cell
2x2 tilings
Each unit is randomly rotated by integer multiples of 90 degrees about each axis and randomly mirrored about each Cartesian axis plane (xy, xz, yz).
3x3x3 tilings
Larger tiling [POVRay source]



 Contribution by Robert McGrego
 Contribution by Robert McGrego
Block tilingWritten by Paul BourkeDecember 2006
 2D tiling ... actually an orthographic projection of a 3D model
 Perspective from the same position as above
 Perspective projection from another position POVRay scene file: blocktile.pov
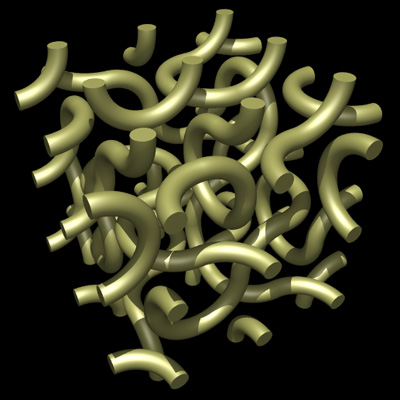
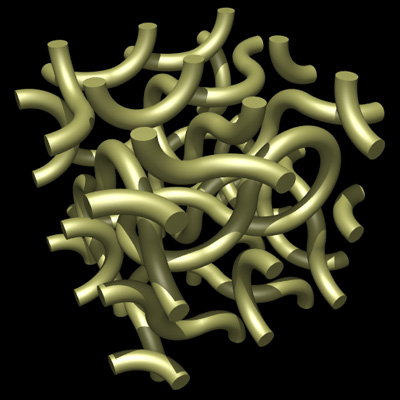
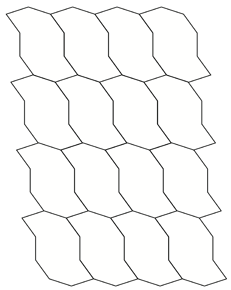
WeaveWritten by Paul BourkeInspired by work by Quincy Kim December 2006
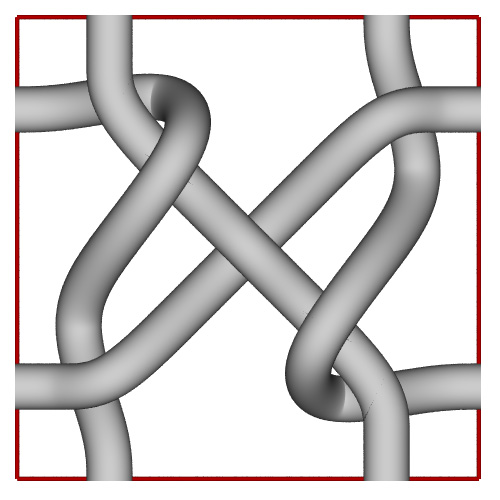 Single tiling unit (Unit square in red).
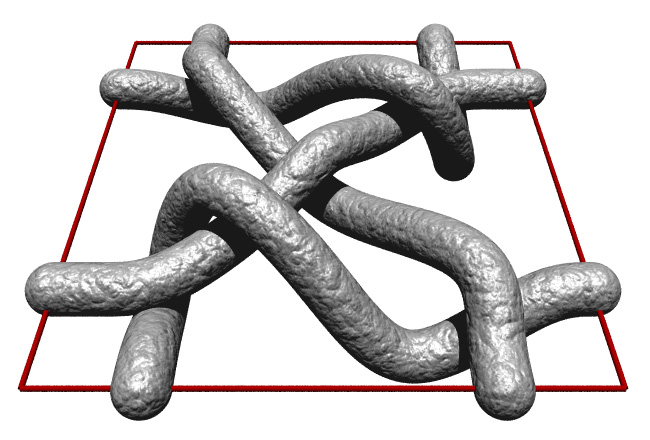 Perspective view of single tiling unit.
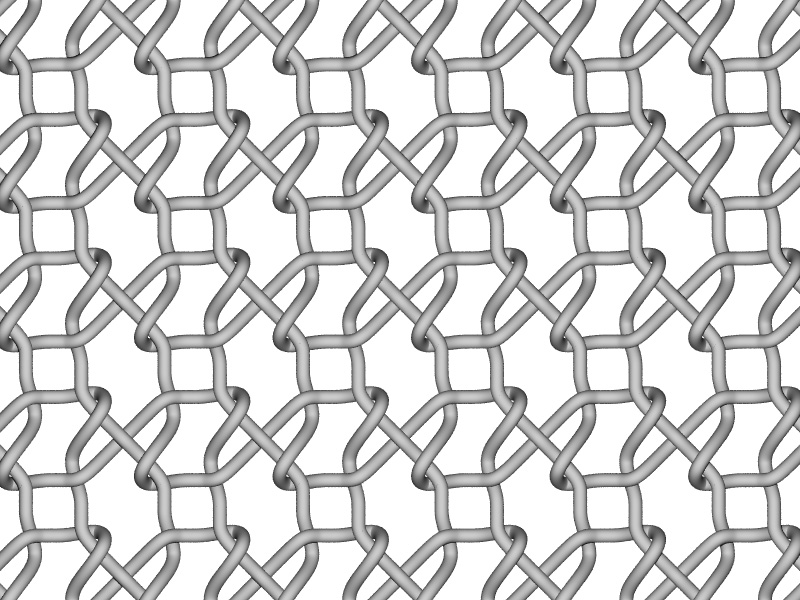 Regular tiling.
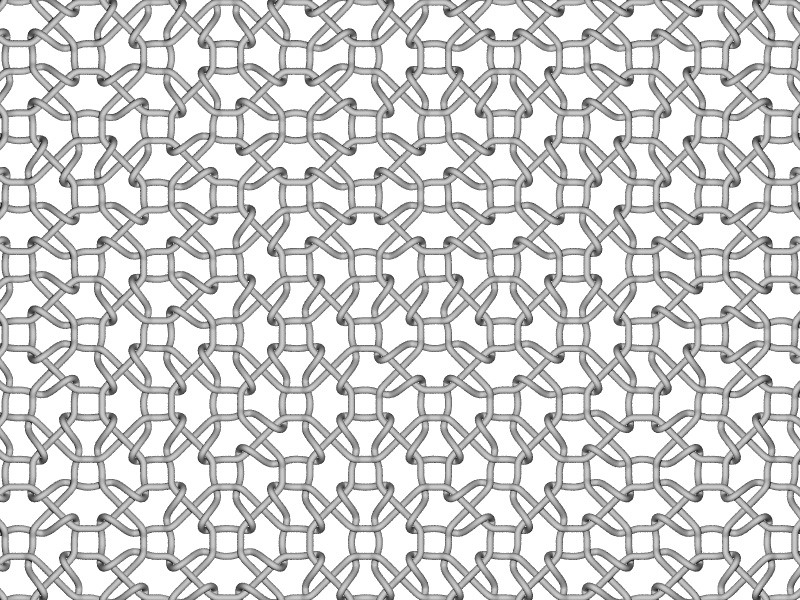 Randomized tiling.
 Perspective view of the randomized tiling.
POVRay scene file: weave.pov for the single unit.
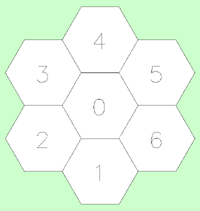
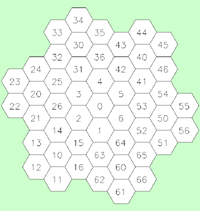
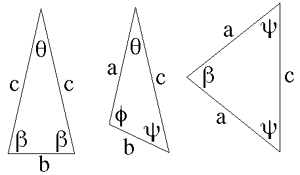
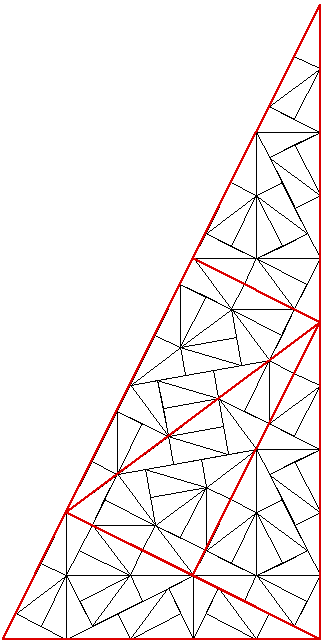
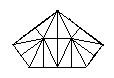
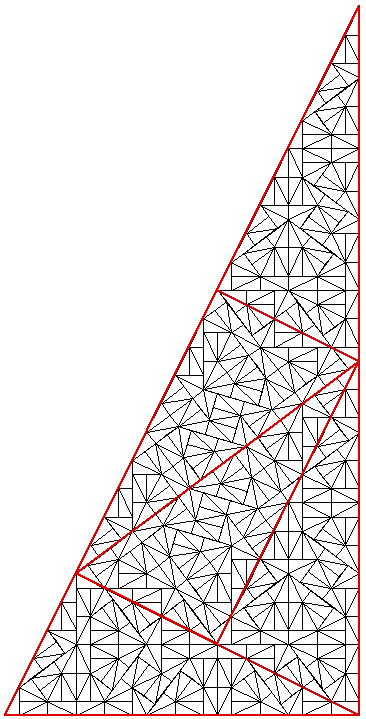
Of the three 2 dimensional shapes (equilateral triangle, rectangle, and hexagon) that can be used to tile the plane without holes, the hexagon is the most complex and has many interesting properties. In what follows, an indexing system will be described for a hexagonal tiling called a Spiral Honeycomb Mosaic (SHM). A SHM consists of groups of 7n hexagons (n > 0) called super-hexagons. It uses a base 7 numbering system for the hexagonal mesh, this is illustrated below for n = 1, 2, and 3.
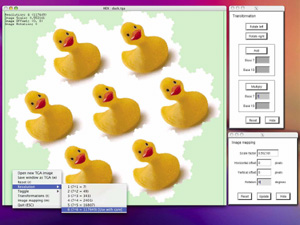
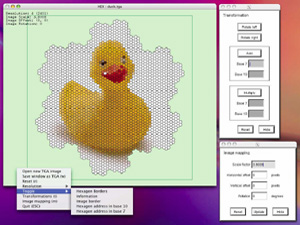
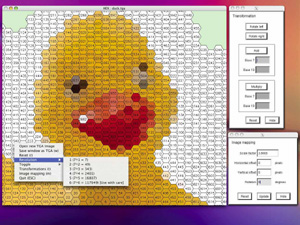
An application has been developed to explore operations in SHM space. Discontinued.
The interface is straightforward, to find out about any command line options type "hex -h". The left mouse button pans the image, the middle button rolls, and the right button presents a list of menu options. In order to position/rotate/scale the hexagon to the image see the image mapping dialog box. To experiment with SHM operations see the transformation dialog box.
>hex -h
Usage: hex [options]
Options
-h this text (help)
-i s load input TGA file
-v verbose mode
Key commands
-,+ zoom in/out
r reset
w write TGA image of window contents
1..6 set resolution
ESC quit
Mouse buttons
left translate
middle rotate
right menus
Addition and Multiplication
The two basic arithmetic operations can be defined for the SMH, addition and multiplication. These operations act on the addresses of the SHM and result in translation (addition) and rotation/scaling (multiplication) when applied to images represented with the "pixels" of the SHM. The following two C snippets (HexAdd() and HexMul()) implement addition and multiplication. An important characteristics of the operations defined in this way is they are bijective, that is, it is a one to one mapping of each address. Every address (hexagonal pixel) maps uniquely to another address so that no information is lost. Examples
The curve through powers of 7 (10hex) is an equiangular spiral described by a = sqrt(3) Since the angle in the above case is taken from the negative y (imaginary) axis, the curve would be traced by y = - r cos(theta) The angle between each successive multiples of 10hex is arctan(sqrt(3) / 2) = 40.893395o, the ratio of two successive radii is sqrt(7) = 2.6457513. Online SHM Calculator
References
Alexander, D. and Sheridan, P.
Sheridan, P.
Sheridan, P., Alexander, D.M.
Sheridan, P., Hintz, T., Alexander, D.
Tiling a plane with single geometric shapes is an old exercise in geometry. The platonic solids were shapes that tile 3D space using regular polyhedra, in 2 dimensions examples of regular polygons that tile (without gaps or overlap) the plane are the equilateral triangle, square, and hexagon. Periodic tilings
There are many examples of general polygons (not regular) that tile the plane, but in the most common cases they form periodic tiling. A periodic tiling is one where it is possible to make a parallelogram (generally larger than the tiles) that can be repeated to produce the same tiling. An example of the more common periodic tiling is shown below for two tiles (blue and yellow), the red boundary illustrates one possible region that can be replicated to create the same effect as the tiles. Note that in general the period forming shape need not be a rectangle but any parallelogram. Note also that there are generally a large, if not infinite, number of periodic parallelograms for a particular periodic tiling. 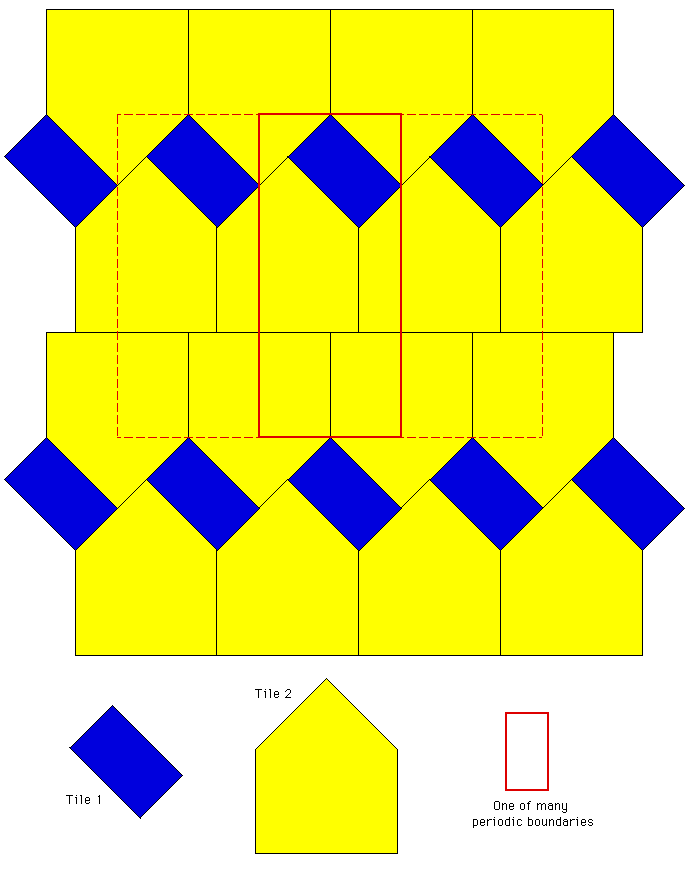 Periodic and nonperiodic
An example of a single tile that can tile periodically and nonperiodically is a decagon (ten sided) with a "bite" taken out of it. Tiles that can form both periodic and nonperiodic tilings are often referred to as "versatile" tiles. 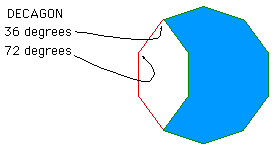
An example of this tiled periodically is given below. Note that for a tiling not to have holes all the angles at a vertex must sum to 360 degrees. In this case each angle is either 72, 144, or 216 degrees. A number of combinations of these numbers can sum to 360. 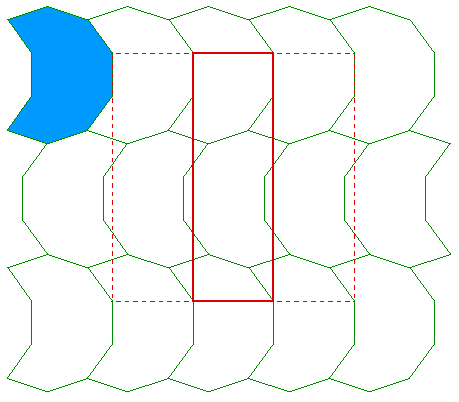
The periodic tiling as shown above have the decagons orientated in multiples of 180 degrees. If the decagons are rotated in multiples of 36 degrees (10 different orientations) the tilings can become nonperiodic as shown below. 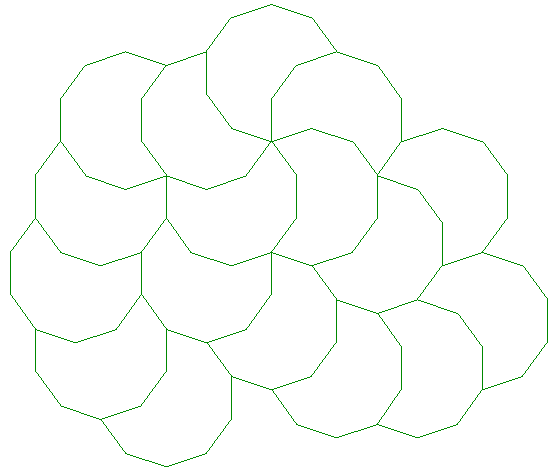
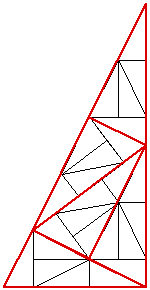
Some shapes that can be combined to form larger versions of themselves have an obvious nonperiodic tiling, for example the following is called the sphinx. A periodic tiling with the same tiles is obvious. For more information on this tiling see Entropy and chirality in sphinx tilings by Greg Huber, Craig Knecht, Walter Trump and Robert M. Ziff. 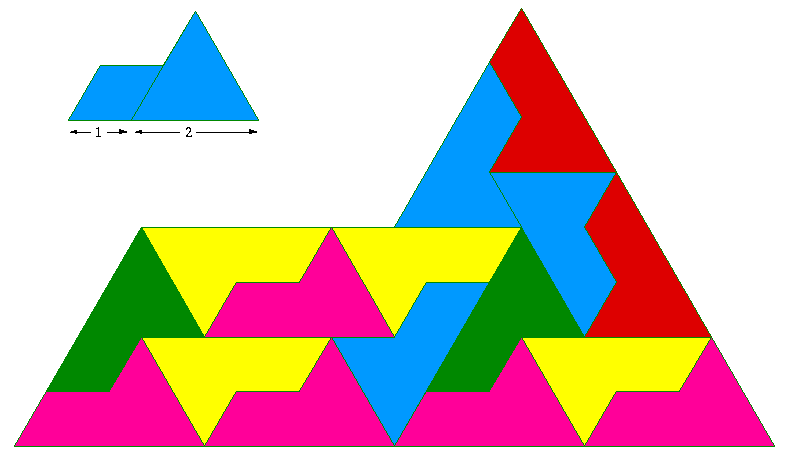 Nonperiodic only
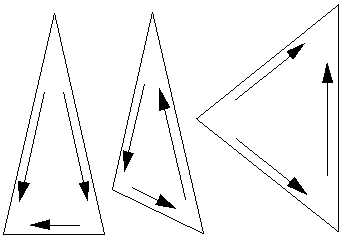
How about purely non periodic tiling, that is, a set of polygons that tile the plane but never form a periodic tiling. For quite a while it was assumed that any set of tiles that formed a non periodic tiling could also be used to form a periodic tiling. In 1966 Robert Berger showed that it was not possible to determine whether a particular set of tiles would tile non periodically! This following set of six nonperiodic tilings were "discovered" by Roger Penrose around 1973. It is illustrative to print and cut a few sets of these tiles out and "experience" how they tile the plane.

The following six tiles are attributed to Richard Robinson who in 1971 reduced a 104 aperiodic tile set by Robert Berger (they were a reduction from a set of originally 20426) to just six tiles.
Around 1973/74 Roger Penrose found a set of two tiles that only tile non periodically. While these come in a number of forms the most common one is illustrated below. Note that phi indicated below is the golden ratio of (1 + sqrt(5))/2. 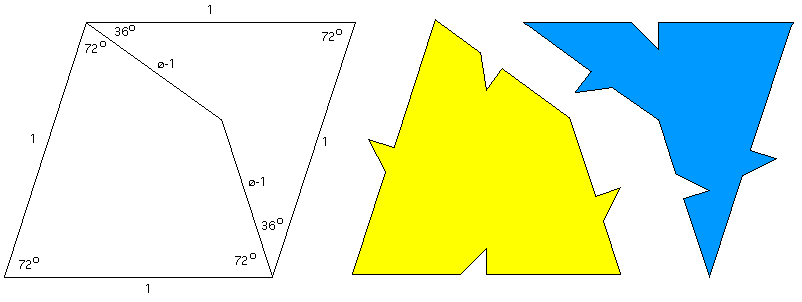 The start of the tiling of these two tiles is illustrated below. The two tiles are often referred to as the kite and dart. The rhombus would of course tile periodically, the triangular pieces force a select combination of allowed connections. 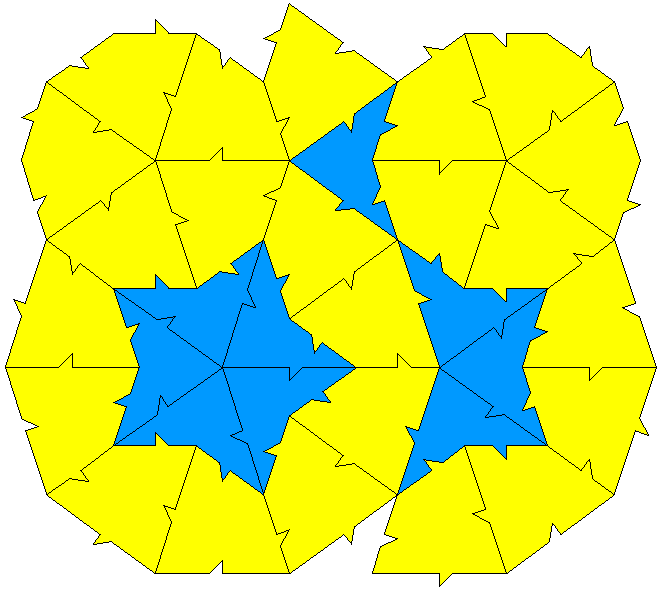 There are a number of elegant properties of this tiling. For example, the ratio of kits to darts in an infinite tiling is the golden ratio! Another two tile non periodic tiling by Roger Penrose
  Floor of the Chemistry building, University of Western Australia.
Chair Aperiodic TilingWritten by Paul BourkeJune 2000

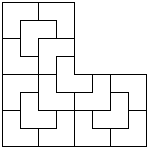
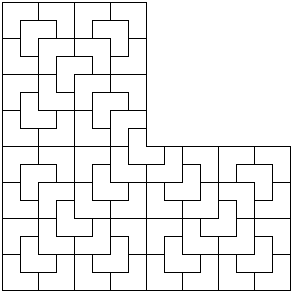
Trilobite - Cross aperiodic tilingWritten by Paul BourkeJune 2002
Constrained decagon tilesInspired by Dave SmithMarch 2015
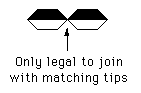
The basic tiling unit is shown below, the constraint is that two semi circles cannot be placed adjacent to each other. All angles are integer multiples of 36 degrees, similarly rotations of the tiling unit are also multiples of 36 degrees. All edge lengths are equal. 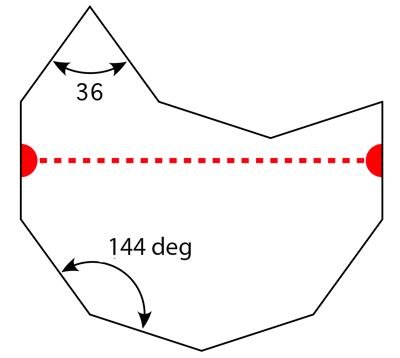
A legal tiling might be as follows. Question: can this tile the plane indefinitely? 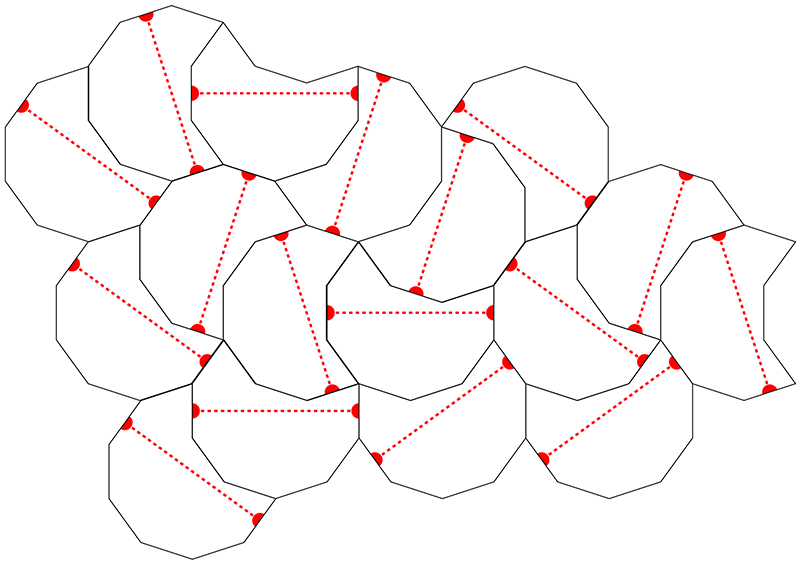
The basic tiling unit is shown below, the internal angles are integer multiples (as shown) of 30 degrees. All edge lengths are equal. 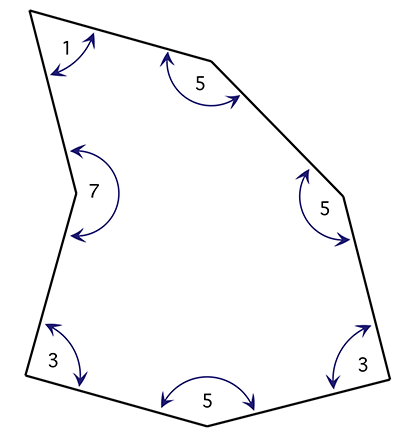
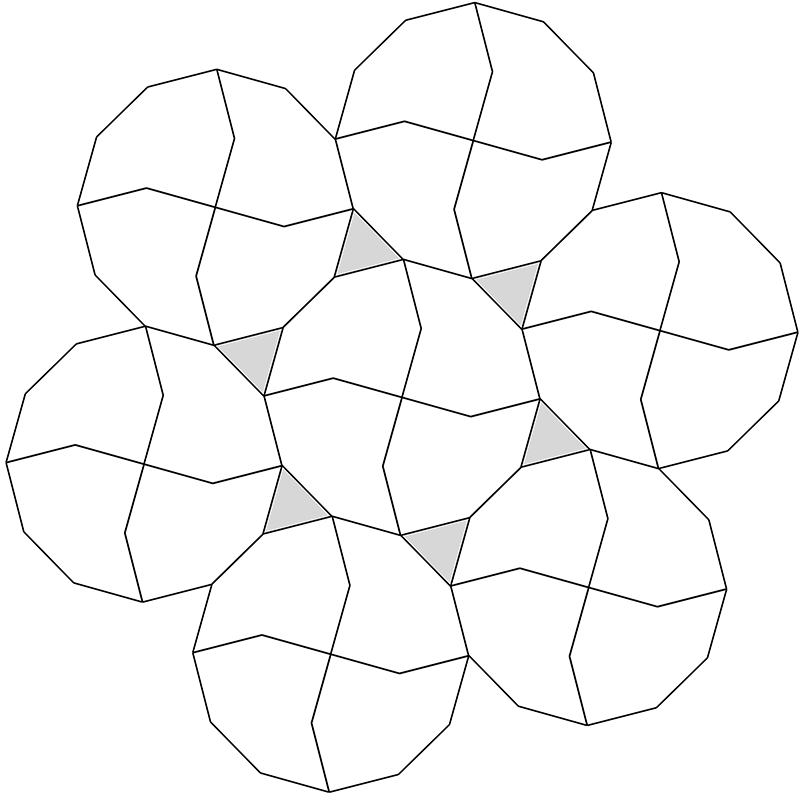
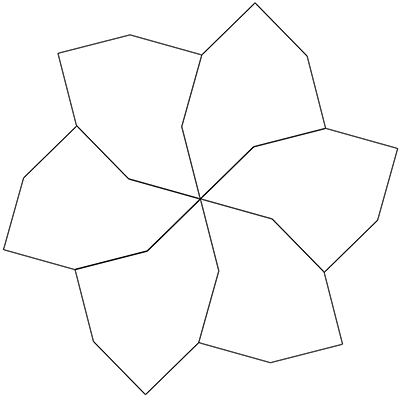
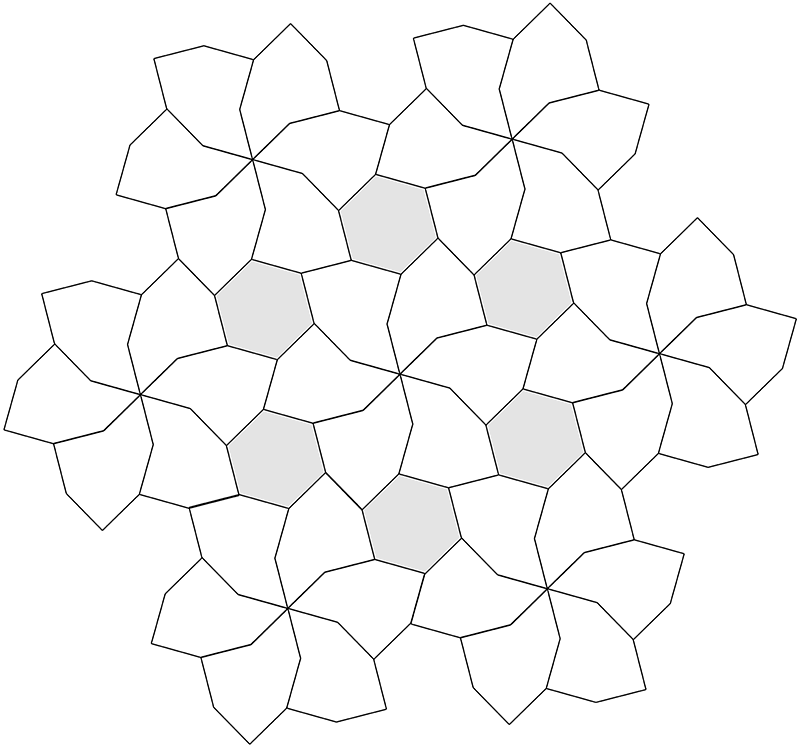
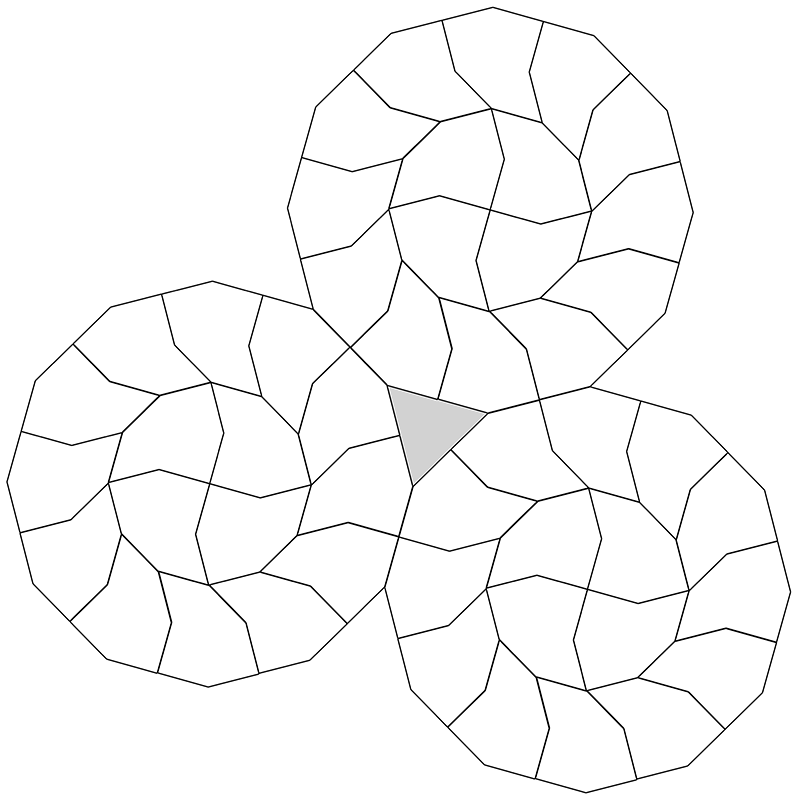
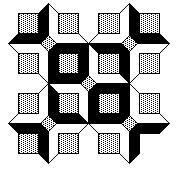
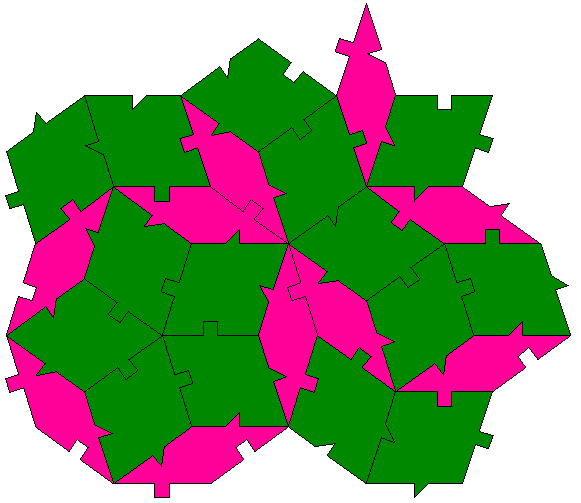
Modified decagon tilesInspired by Dave SmithOctober 2022
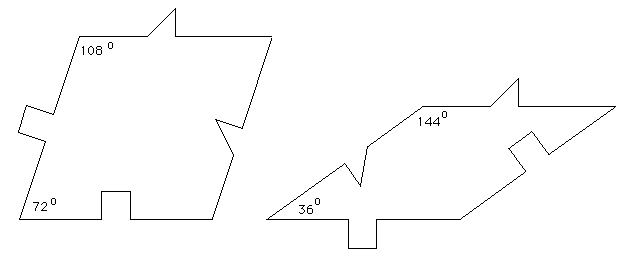
The following tiling takes a decagon (10 sided polygon), removes a bite from one side, bisects the result and mirrors one half to form the "S" shape illustrated below. 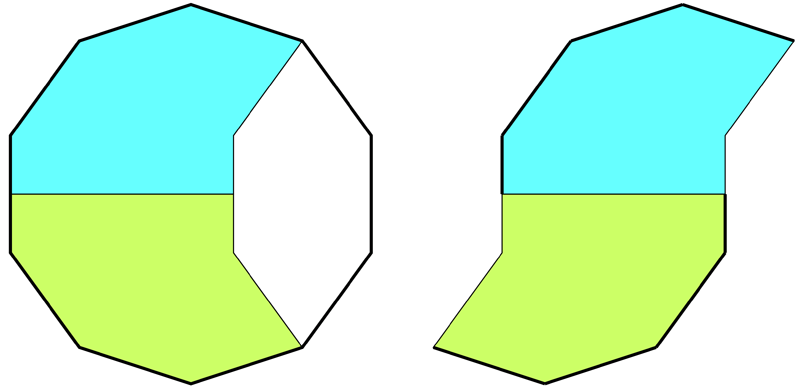
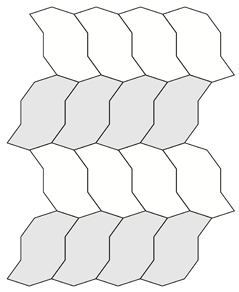
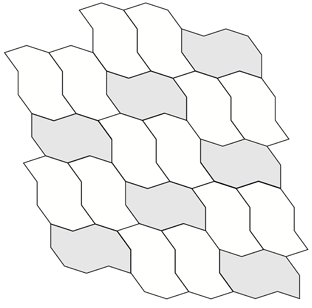
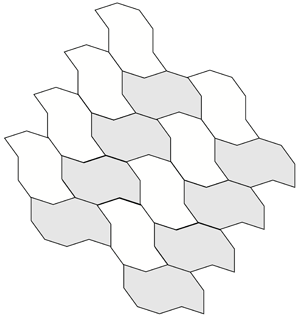
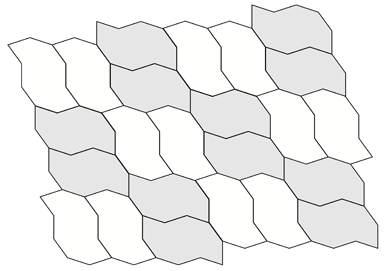
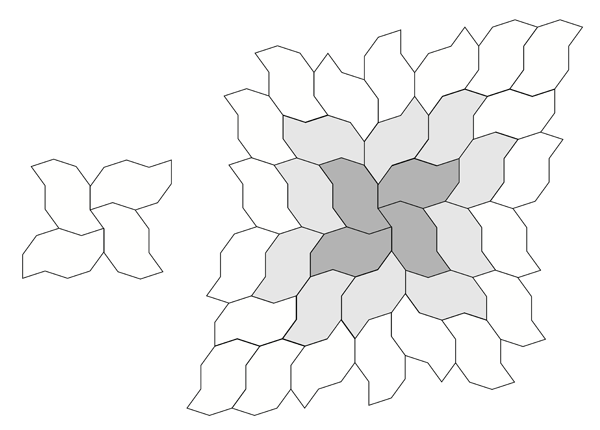
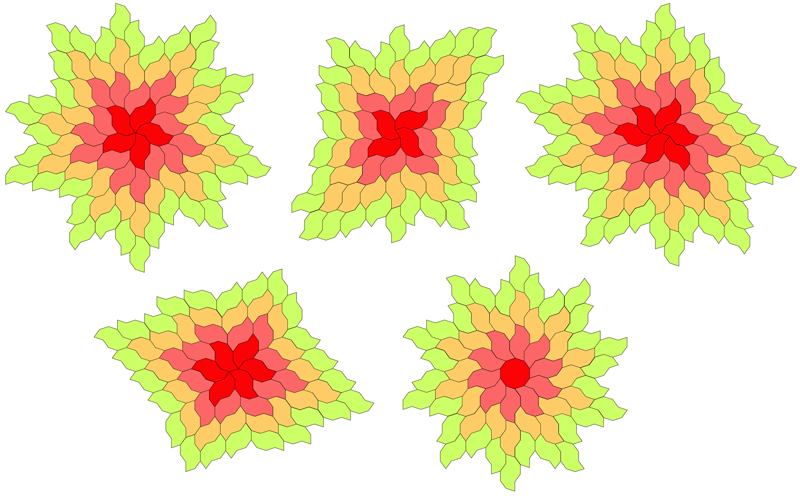
A number of regular tilings can be created, a selection are shown below.
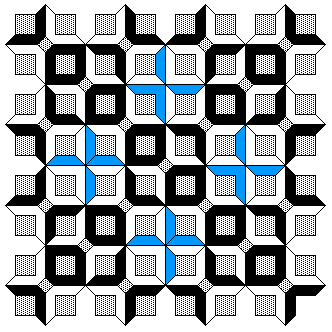
Tilings based upon 4 different initial configurations. 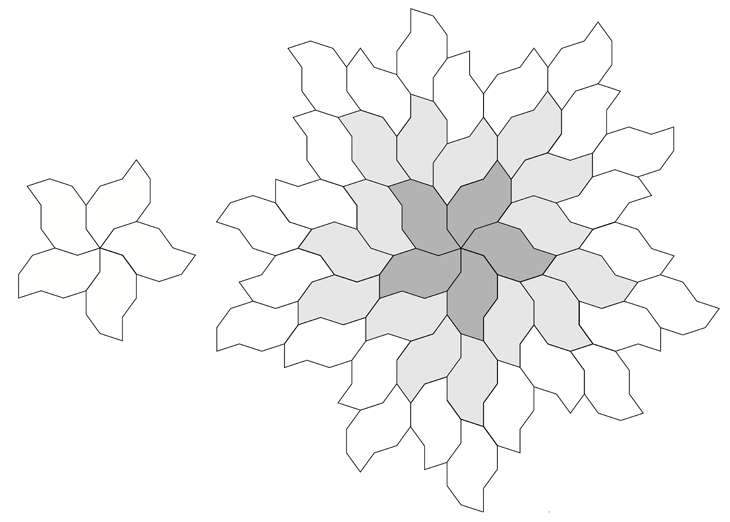
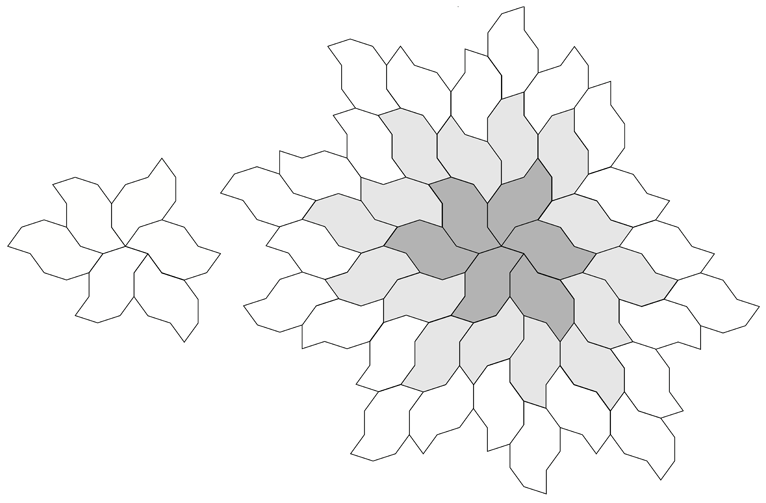
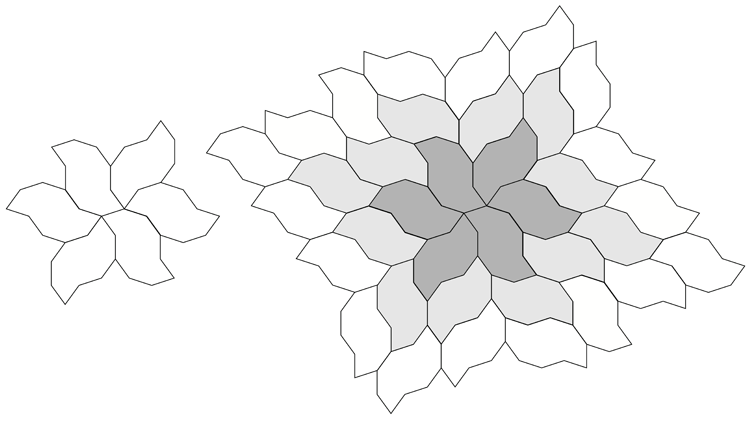
A tiling around the original central decagon. 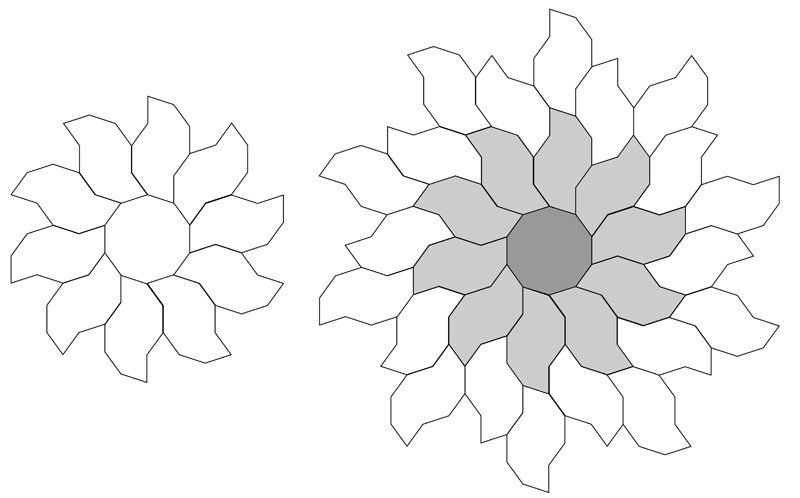
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||