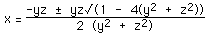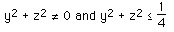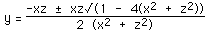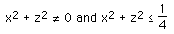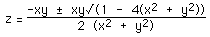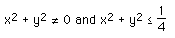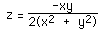Steiner surface
Also known as the Roman Surface
Written by Paul Bourke
August 1988
The Steiner surface is attributed to Jacob Steiner, created while he
was visiting Rome in 1844.
Points on the so called Steiner surface satisfy the following equation in 3
space.
x2 y2 + x2 z2 +
z2 y2 + xyz = 0
This surface is relatively interesting but hard to visualise without 3D views.
The method used here will place markers
(spheres) at points on the surface, these can
then be rendered with most rendering software.
Solving for x
Rearranging, the equation of the Steiner surface can be written as a quadratic
in x, namely
x2 (y2 + z2) + (y z) x +
y2 z2 = 0
solving this quadratic in x gives
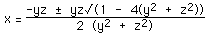
solutions exist as long as
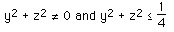
The first condition is only satisfied if x and y are 0. The second condition
means that solutions only exist for points within a circle in the yz
plane.centered at the origin and radius 0.5.
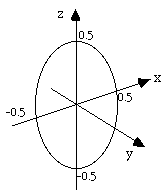
From symmetry, similar equations can be derived for y and z.
Solving for y
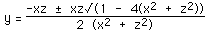
solutions exist as long as
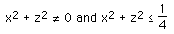
Solutions only exist for points within a circle in the xz plane.centered at the
origin and radius 0.5.
Solving for z
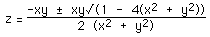
solutions exist as long as
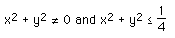
Solutions only exist for points within a circle in the xy plane.centered at the
origin and radius 0.5.
Notes
From the original equation it can be seen that the surface passes through the
point (0,0,0).
The surface lies within a sphere at the origin of radius 0.5
At the points where the circle in each plane crosses the axes, the Steiner
surface is 0 in the axis perpendicular to the surface.
The equation of the surface around the circle on one of the planes is of the
form (for the xy plane)
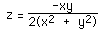
If the circle is flattened out this curve looks like a skewed sine function.
Visualisation
To visualise this surface one might sample it on a mesh in each of the planes:
xy, yz, zx. The pseudo code for the xy plane samples might be as follows. The
smaller the grid size, delta, the finer the sampling of the surface.
for x=-0.5 to 0.5 step delta
for y=-0.5 to 0.5 step delta
if x*x + y*y is not 0 then
if 1 - 4 (x*x + y*y) is greater than or equal to 0
evaluate the two values of z
draw something at the two positions
end if
end if
end for
end for
The equivalent sampling can be performed for the other two planes. The
markers placed in space should be checked against the ones already found to
avoid placing two markers in the same position. In the diagrams below small
spheres were placed at each position on the surface, any sphere that
intersected another by more than a certain amount was ignored.
Images of the Steiner surface rendered using the Radiance software are shown
below.

View of the surface with the camera at (1,0.5,0) pointing towards
the origin.

View of the surface and border with the camera at (1,1,1) pointing towards the
origin
Parametrisation
The parametric form of the Steiner surface is as follows:
x = cos(v) cos(v) sin(2u) / 2
y = sin(u) sin(2v) / 2
z = cos(u) sin(2v) / 2
where 0 <= u <= pi, 0 <= v <= pi
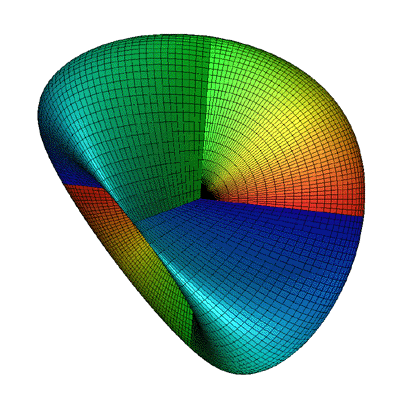



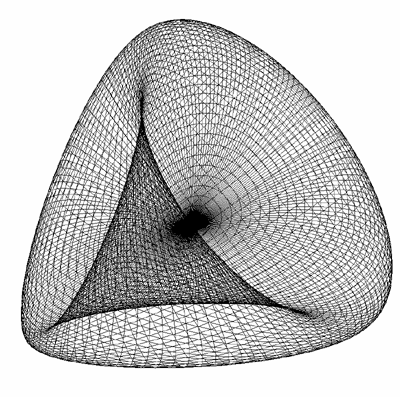
Steiner Look-A-Like
Designed by Roger Bagula
Graphics and C code by Paul Bourke
September 2000
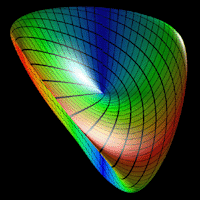
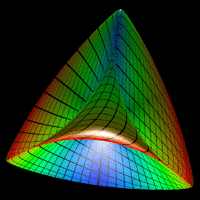
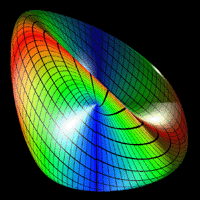
| |
|
Nonlinear Differential Twisting of the Angular Triangle as Minimal 3
Dimensional Parametric Function
by Roger L. Bagula 18 Sept 2000©
Abstract: A new nonlinear surface definition that appears to be very
like a Steiner surface
It is based on the differential twisting of the
angular triangle minimal
coordinate surface.
Partial angular differentiation in self-similar and affine fractal
IFS's has appeared in previous TFTN articles. In this is meant:
1) cos(t)=sin(t-Pi/2)
2) dcos(t)= -sin(t)*dt
3) f(t,s)=cos(t+Pi*s/2): domain: {s: 0,1}
Applying this kind of partial angular differential to the surface:
4) x=cos(2*Pi*t-s*Pi/2)*cos(2*Pi*(-t+p)+s*Pi/2)
5) y=cos(2*Pi*p-s*Pi/2)*cos(2*Pi*(-t+p)+s*Pi/2)
6) z=cos(2*Pi*p-s*Pi/2)*cos(2*Pi*t-s*Pi/2)
Unless s is a function of the two angular plane variables it appears as
a new variable.
Experiments were done with different dependent versions for s and a
mistake was made to get:
7) s' = s + p - s * p
which is an entropic fuzzy logic type of function in a nonlinear form
for s. The result in terms of the surface was to remove one lobe of the
original surface.
That the surface has an appearance like a Steiner surface or may even
be another
definition of a Steiner surface makes the original Angular Triangle as
Minimal (ATM)
surface more important and interesting as well.
It was a result of work in trying to get a Fano finite projective
plane to express as a three dimensional surface using angular plane
lines in a partition function. The suggestion is that
the ATM surface is twisting of the topological projective plane that the
Steiner surface represents and thus, is a new class of such surfaces. It
may in fact be a more fundamental
version of such fundamental topological surfaces, since it uses a more
minimal definition in its coordinates.
This new procedure also represents a new kind of nonlinear coordinate
procedure to
produce surfaces which can be generalized even further to:
8) s' = f(s,t,p)
This specific transform in 7) seems to leave both the cylinder and
sphere invariant in experiments in my True Basic projections. More
experiments would be necessary to get a better view of such nonlinear
functions in s, but it seems to be a phase angle twisting that has to be
just right for the symmetry of the surface.
The angular plane approach to surface geometry has resulted in a whole
new variety of surfaces and the ATM surfaces seem to be the most
fundamental results so far.
|
Source Code
|