Mathematics of the Meta Logo

Late in 2021 Facebook rebranded the company and adopted a new name "Meta". This included a new logo, the generally accepted versions in 2D and 3D are shown below.

The question then might be, what is the equation underlying this new logo? The most obvious candidate for the equation would be the following, essentially a Lissajous style curve defined as follows.

The following is an orthographic projection (all images in this document will be orthographic unless stated otherwise) with the shape rotated 35 degrees about the vertical axis, the value of A is 0.8.

While this is not a match to the Meta logo, the extreme lobes are too sharp, it does however work for other similar logos, such as the Sense logo.

And the MileniumGroup logo.

With A = 0.3 and a view from 45 degrees off the coordinate axis, it serves as a representation of the infinity symbol.

Which has been used in the past by another company of the same name.

Or by Infinity Endless Soap.

Another candidate might be the equation for the baseball seam.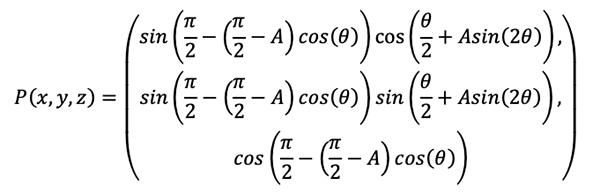

The representation below is with A = 0.43.

But it does not seem like a straightforward modification to pull out the lobes. One gets something closer by taking the intersection of the Ennepers minimum surface with a sphere. The Enneppers minimal surface is defined as: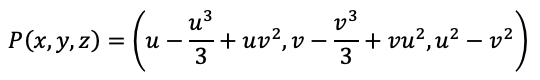

And the intersection with a sphere of radius 0.13 (and then thickened) gives the following.

But still not quite right. The flattening of the lobes is still elusive. It is a similar effect to the Metta logo below.

Where a simplistic periodic function such as the following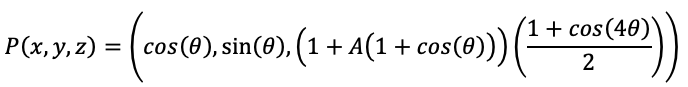

Fails to capture the wide lobes.

At the end of the day the logo may not have a simple closed equation form since there is a suggestion that it may have been created from a 3D drawing tool within a VR environment. As such it is most likely based upon some type of spline curve, perhaps created with something like "Gravity Sketch" on Quest 2 using a series of tweaked splines. It was then almost certainly cleaned up thus losing any clean mathematical formulation.

Along these lines, this is a Hermite interpolation of a 5 point polygon with control over tension so the curve can be fattened to match. The Hermite interpolation function is as follows

/*
   Tension: 1 is high, 0 normal, -1 is low
   Bias: 0 is even,
         positive is towards first segment,
         negative towards the other
*/
double HermiteInterpolate(double y0,double y1,double y2,double y3,double mu,double tension,double bias)
{
   double m0,m1,mu2,mu3;
   double a0,a1,a2,a3;

   mu2 = mu * mu;
   mu3 = mu2 * mu;
   m0  = (y1-y0)*(1+bias)*(1-tension)/2;
   m0 += (y2-y1)*(1-bias)*(1-tension)/2;
   m1  = (y2-y1)*(1+bias)*(1-tension)/2;
   m1 += (y3-y2)*(1-bias)*(1-tension)/2;
   a0 =  2*mu3 - 3*mu2 + 1;
   a1 =    mu3 - 2*mu2 + mu;
   a2 =    mu3 -   mu2;
   a3 = -2*mu3 + 3*mu2;

   return(a0*y1+a1*m0+a2*m1+a3*y2);
}

And the points are simply.

XYZ c[7] = {{1,-2,1},{1,0,1},{0,1,-1},{-1,0,1},{0,-1,-1},{1,0,1},{1,2,1}};

This is the best representation found so far, and hardly an elegant solution despite it possibly being close to the original formulation. Readers are welcome to contribute a cleaner soluion.

The equirectangular representation is straightforward.

Navigable version

Perspective views.

Other related logos

Double width logo from a proposal from a third party to Facebook, circa 2014.