Circumference of an EllipseAnd an approximation using arc sectionsCollected by Paul BourkeCorrections and contributions by David Cantrell and Charles Karney.
Update (June 2013) by Charles Karney and
the AGM (Arithmetic Geometric Mean) algorithm.
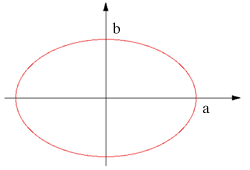 a - Major axis radius b - Minor axis radius e - eccentricity = (1 - b2 / a2)1/2 f - focus = (a2 - b2)1/2 h = (a - b)2 / (a + b)2 area = pi a b
The following lists and evaluates some of the approximations that can be used to calculate the circumference of an ellipse, specifically, shapes defined by the points: 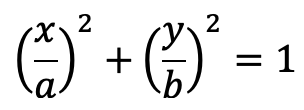
To some, perhaps surprising that there is not a simple closed solution, as there is for the special case of a circle (a=b). Anonymous
Reduces to the circumference of a circle for a=b. This performs the worst for highly eccentric ellipses, for example when b=0 the length is 3.847a rather than the expected value of 4a. 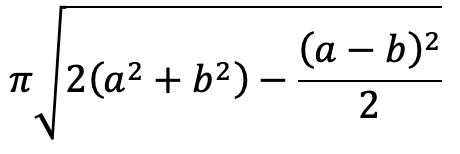
Ramanujan, first approximation
Indian mathematician Srinivasa Ramanujan proposed the following circa 1914. Reduces to the circumference of a circle for a=b. When b=0 the circumference is 3.983a rather than the expected value of 4a. Ramanujan, second approximation
This is one of the more accurate simple approximations presented here although it degrades for large a/b ratios. Reduces to the circumference of a circle for a=b (h=0). For b=0 the circumference is 3.9984a, much closer to the expected value of 4a of the previous expressions. Zafary
Attributed to Shahram Zafary. Reduces to the circumference of a circle for a=b (h=0). Reduces to the correct value of 4a when b=0.
This does not use any computationally expensive functions, such as the square root. Reduces to the circumference of a circle for a=b (h=0). For b=0 the circumference is 3.9924a, compared to the expected value of 4a. 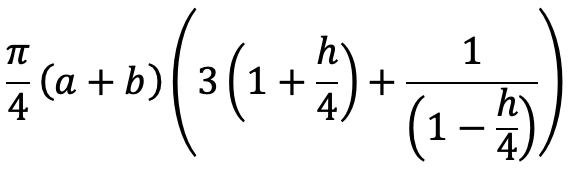
Both the holder mean and Muir case reduces to the circumference of a circle for a=b (h=0). Reduces to the correct value of 4a when b=0. where
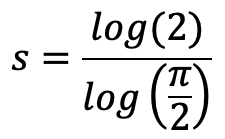
For low eccentricities (Muir, 1883) circumference is. 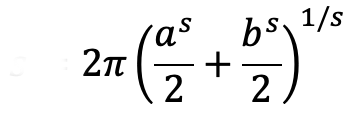
where s = 1.5 David Cantrell
Reduces to the circumference of a circle for a=b. Reduces to the correct value of 4a when b=0. 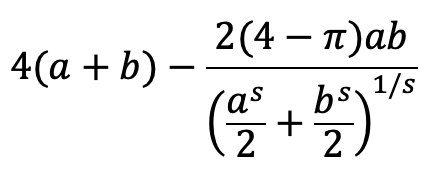
where
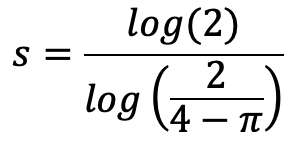
Exact
There is an exact series expansion but it converges rather slowly and it has numerical issues due to the need for large factorials, even if the factorial ratios are computed in pairs. Reduces to the circumference of a circle for a=b (e=0). 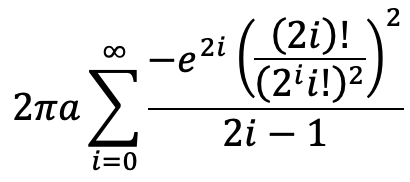
Integral (exact)
The following can be derived directly from the line integral of the equation of an ellipse. Reduces to the circumference of a circle for a=b. 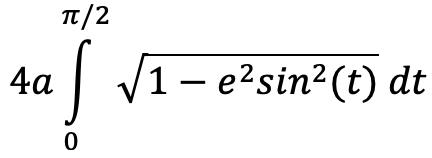
Necat Tasdelen
Various approximations are provided by Necat Tasdelen, they consist of improved estimates of "s" for what is referred to as the Holder method above. Three estimates of "s" are provided in the examples below, a constant value (same as Holder), a linear, and a power fit estimate. The later is one of the more accurate approximations presented here for extreme eccentricities. For the further details the reader is directed to the documents: Ellipse Perimeter Estimation by Necat Tasdelen: Necat.pdf and the equivalent elliptic integrals: elliptic.pdf. Since they are based upon the Holder method, they reduce to the circumference of a circle for a=b. Bessel
Charles Karney contributed this rapidly converging series attributed to Bessel (1825). Reduces to the circumference of a circle for a=b (h=0). 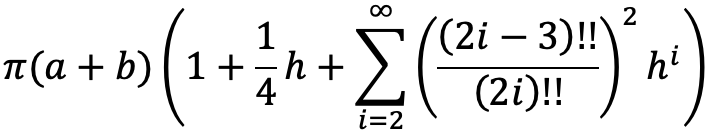
Giovanni Anselmi proposed the following: where n is
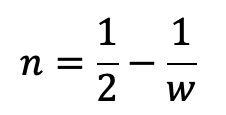 and w is
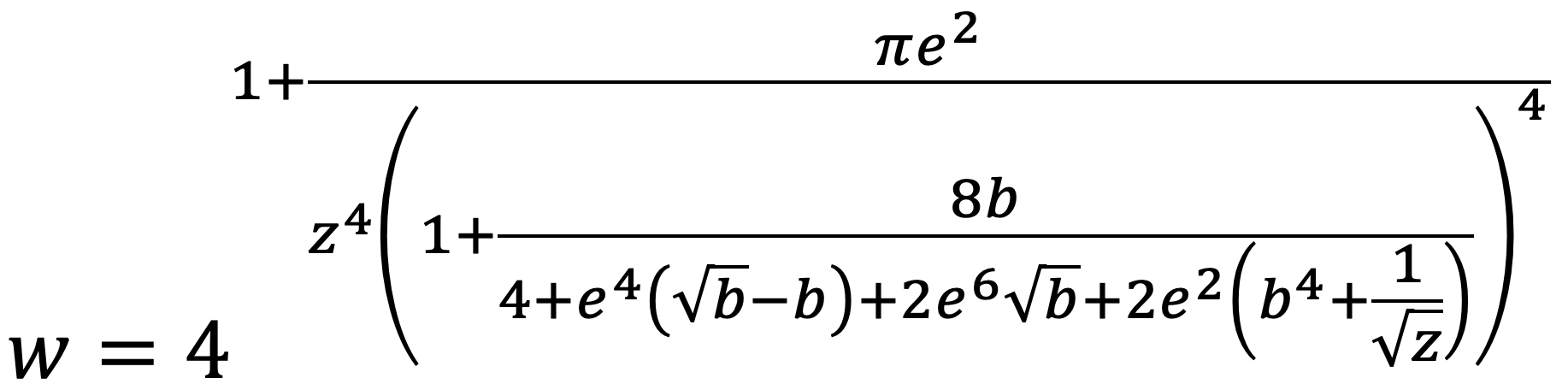 and z is a constant given by
When b=1 (circle) the expression reduces to the circumference of a circle. Reduces to the correct value of 4 when b=0. Note that unlike other expressions here, this requires the major axis "a" is normalised to 1. This is not a problem, before computing the circumference one scales the ellipse by 1/a and scales the resulting circumference value by the original value of "a". Contributions
Paper by Paul Abbott: Abbott.pdf Contribution by Bill Gran: gran.png and a nifty little Excel Calculator: GRAN_Method_Calculator.xlsx.zip. Appears in ANC-5 Strength of Metal Aircraft Elements March 1955 Revised Edition Section 1.535, pages 11-13. GRAN Formula for the Complete Elliptic Integral of the Second Kind. Adjustments to Ramanujan's formula and tables Ramanujan.xls.zip by Hassan Abed, as well as modifications to Hudson formula and correction, and his own approximations AbedsFormulas.xls.zip AGM algorithm contributed by Charles Karney and based upon Carlson, B. C. (1995). "Computation of real or complex elliptic integrals". Numerical Algorithms 10. This algorithm converses quadratically, that is, the number of correct digits doubles on each iteration so the fastest converging series of those presented here. Versions: Maxima, Python and C. The series was first proposed by James Ivory, A new series for the rectification of the ellipsis, Trans. Roy. Soc. Edinburgh 4, 177-190 (1798). Analysis
In the following increasing eccentric ellipses are considered and circumference estimate shown for each approximation, along with the percentage error. The ground truth is the numerical discrete approximation using 10 million line segments, this is referred to as the "numerical" approximation in the following tables. All mathematics is performed using "long double" precision, 16 bytes. In each case "a" the major axis is normalised to unity, for other values of "a" this is just a scaling factor for the final circumference. Also, "a" ≥ "b". Example: a=1, b=1 (Circle)

Not surprisingly, most approximations are perfect since they reduce to the known circumference of a circle when a=b. a : 1.0000000000 b : 1.0000000000 e : 0.0000000000 h : 0.0000000000 b/a: 1.0000000000 Numerical : 6.276727658228 %Error: 0.102776675146 ( 10 segments) Numerical : 6.283120710969 %Error: 0.001028080621 ( 100 segments) Numerical : 6.283184661216 %Error: 0.000010280838 ( 1000 segments) Numerical : 6.283185300720 %Error: 0.000000102808 ( 10000 segments) Numerical : 6.283185307115 %Error: 0.000000001028 ( 100000 segments) Numerical : 6.283185307179 %Error: 0.000000000010 ( 1000000 segments) Integral : 6.911503837898 %Error: 10.000000000000 ( 10 segments) Integral : 6.346017160251 %Error: 1.000000000000 ( 100 segments) Integral : 6.289468492487 %Error: 0.100000000000 ( 1000 segments) Integral : 6.283813625710 %Error: 0.010000000000 ( 10000 segments) Integral : 6.283248139033 %Error: 0.001000000000 ( 100000 segments) Integral : 6.283191590365 %Error: 0.000099999999 ( 1000000 segments) Integral : 6.283185935498 %Error: 0.000009999992 ( 10000000 segments) Integral : 6.283185370018 %Error: 0.000001000099 (100000000 segments) Exact : 6.283185307180 %Error: 0.000000000000 ( 10 terms) Exact : 6.283185307180 %Error: 0.000000000000 ( 50 terms) Exact : 6.283185307180 %Error: 0.000000000000 ( 250 terms) Exact : 6.283185307180 %Error: 0.000000000000 ( 1250 terms) Bessel : 6.283185307180 %Error: 0.000000000000 ( 10 terms) Bessel : 6.283185307180 %Error: 0.000000000000 ( 100 terms) Bessel : 6.283185307180 %Error: 0.000000000000 ( 1000 terms) Anonymous : 6.283185307180 %Error: 0.000000000000 Zafary : 6.283185307180 %Error: 0.000000000000 Hudson : 6.283185307180 %Error: 0.000000000000 Ramanujan 1 : 6.283185307180 %Error: 0.000000000000 Ramanujan 11 : 6.283185307180 %Error: 0.000000000000 Holder mean : 6.283185307180 %Error: 0.000000000000 (s: 1.534928535661) Cantrell : 6.283185307180 %Error: 0.000000000000 (s: 0.829896183163) Necat (constant s) : 6.283185307180 %Error: 0.000000000000 (s: 1.534928535661375) Necat (linear s) : 6.283185307180 %Error: 0.000000000000 (s: 1.534928535661380) Necat (power s) : 6.283185307180 %Error: 0.000000000000 (s: 1.534928535661380) Anselmi : 6.283185307180 %Error: 0.000000000000 Example: a=1, b=1/2

In general the simple minded numerical approximation (adding up increasingly small line segments) improves by 2 decimal points for every factor of 10 of line segment length. The "integral" method generally only improves by one decimal point for every factor ten in "dt". While these two approximation may seem better than most others, they are far and away the most inefficient to compute compared to the closed solutions. a : 1.0000000000 b : 0.5000000000 e : 0.8660254038 h : 0.1111111111 b/a: 0.5000000000 Numerical : 4.839245377805 %Error: 0.102776674976 ( 10 segments) Numerical : 4.844174307745 %Error: 0.001028080621 ( 100 segments) Numerical : 4.844223612247 %Error: 0.000010280837 ( 1000 segments) Numerical : 4.844224105294 %Error: 0.000000102808 ( 10000 segments) Numerical : 4.844224110224 %Error: 0.000000001028 ( 100000 segments) Numerical : 4.844224110273 %Error: 0.000000000010 ( 1000000 segments) Integral : 5.315463008304 %Error: 9.727850885982 ( 10 segments) Integral : 4.891348000078 %Error: 0.972785088615 ( 100 segments) Integral : 4.848936499254 %Error: 0.097278508862 ( 1000 segments) Integral : 4.844695349172 %Error: 0.009727850886 ( 10000 segments) Integral : 4.844271234164 %Error: 0.000972785089 ( 100000 segments) Integral : 4.844228822663 %Error: 0.000097278509 ( 1000000 segments) Integral : 4.844224581513 %Error: 0.000009727851 ( 10000000 segments) Integral : 4.844224157398 %Error: 0.000000972785 (100000000 segments) Exact : 4.845802239648 %Error: 0.032577546755 ( 10 terms) Exact : 4.844224111093 %Error: 0.000000016915 ( 50 terms) Exact : 4.844224110274 %Error: 0.000000000000 ( 250 terms) Exact : 4.844224110274 %Error: 0.000000000000 ( 1250 terms) Bessel : 4.844224110274 %Error: 0.000000000003 ( 10 terms) Bessel : 4.844224110274 %Error: 0.000000000000 ( 100 terms) Bessel : 4.844224110274 %Error: 0.000000000000 ( 1000 terms) Anonymous : 4.841519436353 %Error: 0.055832964349 Zafary : 4.840584564428 %Error: 0.075131657065 Hudson : 4.844223672098 %Error: 0.000009045329 Ramanujan 1 : 4.844210548836 %Error: 0.000279950677 Ramanujan 11 : 4.844224108065 %Error: 0.000000045596 Holder mean : 4.852240815322 %Error: 0.165489970436 (s: 1.534928535661) Cantrell : 4.844274033183 %Error: 0.001030565640 (s: 0.829896183163) Necat (constant s) : 4.852240815322 %Error: 0.165489970436 (s: 1.534928535661375) Necat (linear s) : 4.844020829977 %Error: 0.004196343767 (s: 1.541982035153419) Necat (power s) : 4.844197205706 %Error: 0.000555394781 (s: 1.541829751678717) Anselmi : 4.844146410975 %Error: 0.001603957559 Example: a=1, b=1/5 (Modest eccentricity)
a : 1.0000000000 b : 0.2000000000 e : 0.9797958971 h : 0.4444444444 b/a: 0.2000000000 Numerical : 4.197695801360 %Error: 0.102643918003 ( 10 segments) Numerical : 4.201965707899 %Error: 0.001028080621 ( 100 segments) Numerical : 4.202008475936 %Error: 0.000010280837 ( 1000 segments) Numerical : 4.202008903618 %Error: 0.000000102808 ( 10000 segments) Numerical : 4.202008907895 %Error: 0.000000001028 ( 100000 segments) Numerical : 4.202008907937 %Error: 0.000000000010 ( 1000000 segments) Integral : 4.578994441002 %Error: 8.971554828254 ( 10 segments) Integral : 4.239708019781 %Error: 0.897168774961 ( 100 segments) Integral : 4.205778819122 %Error: 0.089716877496 ( 1000 segments) Integral : 4.202385899056 %Error: 0.008971687750 ( 10000 segments) Integral : 4.202046607050 %Error: 0.000897168775 ( 100000 segments) Integral : 4.202012677849 %Error: 0.000089716878 ( 1000000 segments) Integral : 4.202009284929 %Error: 0.000008971688 ( 10000000 segments) Integral : 4.202008945637 %Error: 0.000000897169 (100000000 segments) Exact : 4.244590771257 %Error: 1.013369182501 ( 10 terms) Exact : 4.202749871108 %Error: 0.017633545909 ( 50 terms) Exact : 4.202008920508 %Error: 0.000000299141 ( 250 terms) Exact : 4.202008907938 %Error: 0.000000000000 ( 1250 terms) Bessel : 4.202008761170 %Error: 0.000003492802 ( 10 terms) Bessel : 4.202008907938 %Error: 0.000000000000 ( 100 terms) Bessel : 4.202008907938 %Error: 0.000000000000 ( 1000 terms) Anonymous : 4.167793630438 %Error: 0.814259994438 Zafary : 4.197182352284 %Error: 0.114863051457 Hudson : 4.201880174176 %Error: 0.003063624192 Ramanujan 1 : 4.201120851870 %Error: 0.021134083420 Ramanujan 11 : 4.202005330312 %Error: 0.000085140846 Holder mean : 4.217215929534 %Error: 0.361898842429 (s: 1.534928535661) Cantrell : 4.202545781069 %Error: 0.012776582412 (s: 0.829896183163) Necat (constant s) : 4.217215929534 %Error: 0.361898842429 (s: 1.534928535661375) Necat (linear s) : 4.201921934184 %Error: 0.002069813640 (s: 1.567399356922549) Necat (power s) : 4.201932915241 %Error: 0.001808484911 (s: 1.567375092439873) Anselmi : 4.202077836898 %Error: 0.001640381115 Example: a = 1, b = 1/10 (High eccentricity)

a : 1.0000000000 b : 0.1000000000 e : 0.9949874371 h : 0.6694214876 b/a: 0.1000000000 Numerical : 4.060042321878 %Error: 0.096749094564 ( 10 segments) Numerical : 4.063932399170 %Error: 0.001028080621 ( 100 segments) Numerical : 4.063973762290 %Error: 0.000010280837 ( 1000 segments) Numerical : 4.063974175923 %Error: 0.000000102808 ( 10000 segments) Numerical : 4.063974180059 %Error: 0.000000001028 ( 100000 segments) Numerical : 4.063974180100 %Error: 0.000000000010 ( 1000000 segments) Integral : 4.409301133354 %Error: 8.497272323820 ( 10 segments) Integral : 4.098531699290 %Error: 0.850338059693 ( 100 segments) Integral : 4.067429932020 %Error: 0.085033805969 ( 1000 segments) Integral : 4.064319755293 %Error: 0.008503380597 ( 10000 segments) Integral : 4.064008737620 %Error: 0.000850338060 ( 100000 segments) Integral : 4.063977635853 %Error: 0.000085033806 ( 1000000 segments) Integral : 4.063974525676 %Error: 0.000008503381 ( 10000000 segments) Integral : 4.063974214658 %Error: 0.000000850338 (100000000 segments) Exact : 4.142030490115 %Error: 1.920689122401 ( 10 terms) Exact : 4.070623873691 %Error: 0.163625389711 ( 50 terms) Exact : 4.064052842541 %Error: 0.001935603847 ( 250 terms) Exact : 4.063974180296 %Error: 0.000000004799 ( 1250 terms) Bessel : 4.063963178517 %Error: 0.000270709995 ( 10 terms) Bessel : 4.063974180101 %Error: 0.000000000000 ( 100 terms) Bessel : 4.063974180101 %Error: 0.000000000000 ( 1000 terms) Anonymous : 3.992419204913 %Error: 1.760714316004 Zafary : 4.062296751651 %Error: 0.041275568588 Hudson : 4.063151007270 %Error: 0.020255365661 Ramanujan 1 : 4.060552518514 %Error: 0.084194963727 Ramanujan 11 : 4.063927210019 %Error: 0.001155767235 Holder mean : 4.075658566530 %Error: 0.287511335250 (s: 1.534928535661) Cantrell : 4.063266238102 %Error: 0.017419943323 (s: 0.819493675057) Necat (constant s) : 4.075658566530 %Error: 0.287511335250 (s: 1.534928535661375) Necat (linear s) : 4.064117543670 %Error: 0.003527669301 (s: 1.591286056206585) Necat (power s) : 4.063991083865 %Error: 0.000415941709 (s: 1.591960989144423) Anselmi : 4.063894898774 %Error: 0.001950832457 Example: a = 1, b = 1/100 (Extreme eccentricity)
The limit of the circumference as "b" tend to zero (a=1) is 4. a : 1.0000000000 b : 0.0100000000 e : 0.9999499987 h : 0.9607881580 b/a: 0.0100000000 Numerical : 4.000698978275 %Error: 0.009981045583 ( 10 segments) Numerical : 4.001059676203 %Error: 0.000966072733 ( 100 segments) Numerical : 4.001097918376 %Error: 0.000010280838 ( 1000 segments) Numerical : 4.001098325609 %Error: 0.000000102808 ( 10000 segments) Numerical : 4.001098329682 %Error: 0.000000001028 ( 100000 segments) Numerical : 4.001098329722 %Error: 0.000000000010 ( 1000000 segments) Integral : 4.312638787661 %Error: 7.786373447112 ( 10 segments) Integral : 4.032825903432 %Error: 0.792971606675 ( 100 segments) Integral : 4.004271338303 %Error: 0.079303439172 ( 1000 segments) Integral : 4.001415630581 %Error: 0.007930343917 ( 10000 segments) Integral : 4.001130059808 %Error: 0.000793034392 ( 100000 segments) Integral : 4.001101502731 %Error: 0.000079303439 ( 1000000 segments) Integral : 4.001098647024 %Error: 0.000007930344 ( 10000000 segments) Integral : 4.001098361453 %Error: 0.000000793034 (100000000 segments) Exact : 4.106968104218 %Error: 2.646017812383 ( 10 terms) Exact : 4.020777220942 %Error: 0.491837230612 ( 50 terms) Exact : 4.004695632675 %Error: 0.089907886677 ( 250 terms) Exact : 4.001642322922 %Error: 0.013596096747 ( 1250 terms) Bessel : 4.000314029813 %Error: 0.019602115344 ( 10 terms) Bessel : 4.001098257191 %Error: 0.000001812804 ( 100 terms) Bessel : 4.001098329723 %Error: 0.000000000000 ( 1000 terms) Anonymous : 3.860645423541 %Error: 3.510358771707 Zafary : 4.001913028601 %Error: 0.020361880947 Hudson : 3.995390384109 %Error: 0.142659468550 Ramanujan 1 : 3.987413450574 %Error: 0.342028063812 Ramanujan 11 : 4.000142159433 %Error: 0.023897695349 Holder mean : 4.002218453588 %Error: 0.027995409585 (s: 1.534928535661) Cantrell : 4.001092914447 %Error: 0.000135344717 (s: 0.819493675057) Necat (constant s) : 4.002218453588 %Error: 0.027995409585 (s: 1.534928535661375) Necat (linear s) : 4.001169590457 %Error: 0.001781029313 (s: 1.657292623796802) Necat (power s) : 4.001145427084 %Error: 0.001177110829 (s: 1.661301486095352) Anselmi : 4.001163383999 %Error: 0.001625910466 Considering ratios of a/b from 1 to 100, one can calculate the maximum percentage error for each approximation, and the value of "b" at which it occurs, "a"=1. Note in the following values of b of 0.01 means the approximation is performing worst for highly elliptical cases.
Approximation of an ellipse using arcsA constructional method for drawing an ellipse in drafting and engineering is usually referred to as the "4 center ellipse" or the "4 arc ellipse". It is a procedure for drawing an approximation to an ellipse using 4 arc sections, one at each end of the major axes (length a) and one at each end of the minor axes (length b). This approximation works well for "fat" ellipses (where minor width is not too small with respect to the major axis). The procedure is documented below along with the diagram illustrating the quantities (a,b,L,φ,θ) used in the calculation. The manual construction method is outlined in the following from: Approximating an Ellipse With Four Circular Arcs Tirupathi R. Chandrupatla (Mechanical Engineering Department) Thomas J. Osler (Mathematics Department) Rowan University Glassboro, New Jersey 08028 
The radii for the two arcs are R = (a sin(θ) + b cos(θ) - b) / (sin(θ) + cos(θ) - 1) where
ø = atan(b/a) θ = asin(cos(φ))
The following shows the meaning of the symbols used. 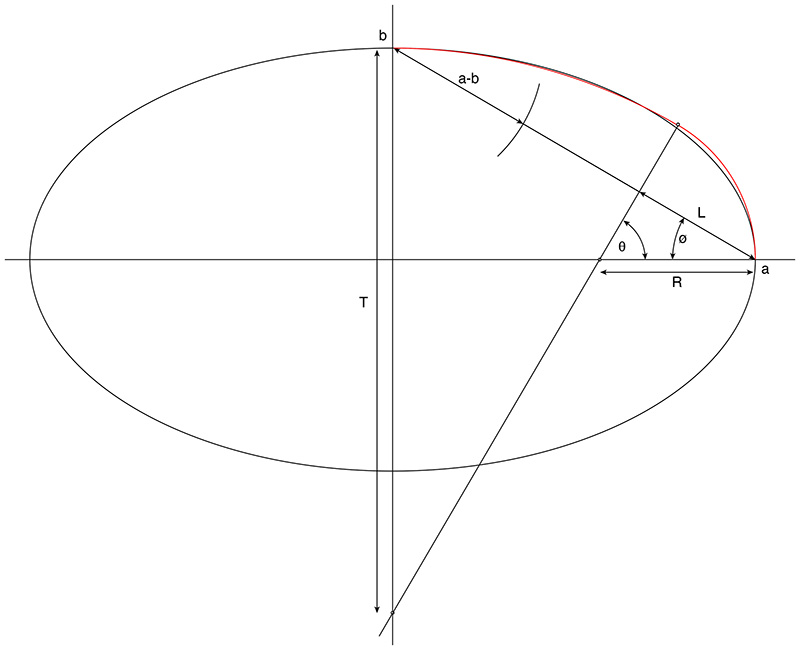
|