Fun with CalculusorPaint bucket that can't be paintedWritten by Paul BourkeJune 1999
Quite often one comes across seemingly mysterious objects in fractal geometry that have, say, zero volume and infinite surface area (see the menger sponge). There are however non intuitive results from more classical calculus and geometry, here's an example.... Consider the curve y = f(x) = 1/x from x=1 to infinity. Now rotate this curve into the z axes, around the x axis to form a curved cone-like object. A plane perpendicular to the x axis that cuts this surface of revolution is a circle with a radius of 1/x. The circumference of this circle is 2pi/x and the area of this circle is pi/x2. This is sometimes known as Gabriel's horn or Gabriel's Trumpet. 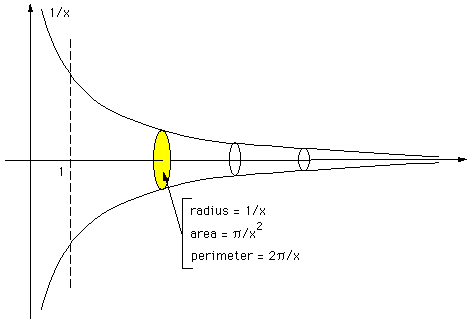
The volume is the integral of pi/x2 with respect to x evaluated between 1 and infinity, this is finite, namely pi. 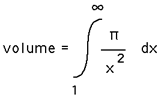
The surface area of our curved cone is infinite. 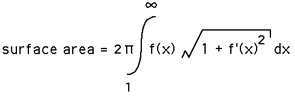
|