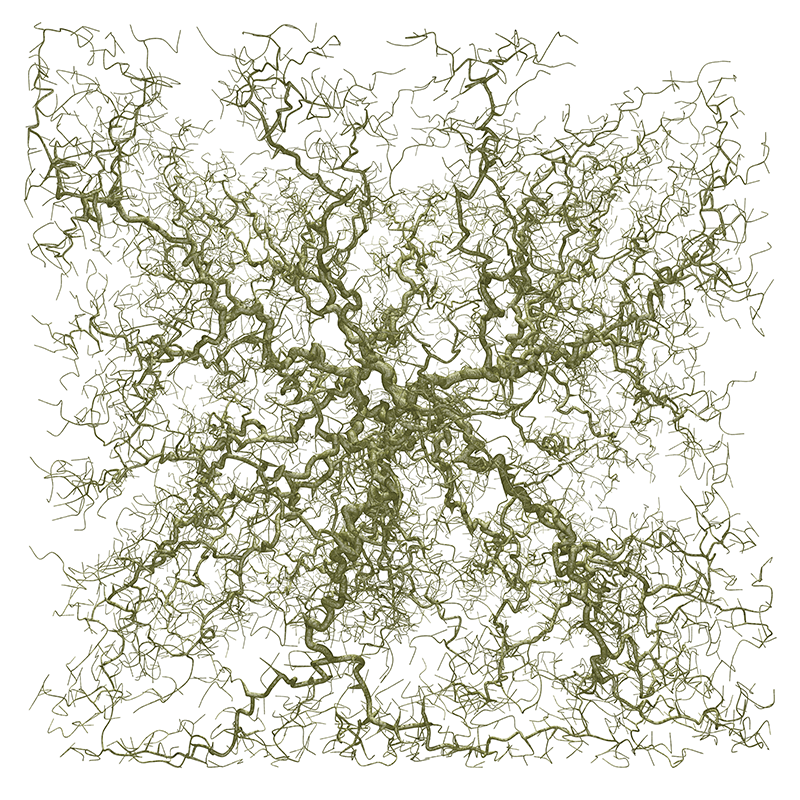
DLA - Diffusion Limited AggregationWritten By Paul BourkeOriginal: June 1991, Updated: January 2004, Updated: Sept 2014 Sample source code (brute force): dla2D.zip
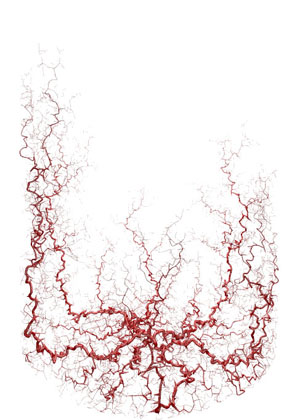
Many attractive images and life-like structures can be generated using models of physical processes from areas of chemistry and physics. One such example is diffusion limited aggregation or DLA which describes, among other things, the diffusion and aggregation of zinc ions in an electrolytic solution onto electrodes. "Diffusion" because the particles forming the structure wander around randomly before attaching themselves ("Aggregating") to the structure. "Diffusion-limited" because the particles are considered to be in low concentrations so they don't come in contact with each other and the structure grows one particle at a time rather then by chunks of particles. Other examples can be found in coral growth, the path taken by lightning, coalescing of dust or smoke particles, and the growth of some crystals. Perhaps the first serious study of such processes was made by Witten, T.A. and Sander, L. M. and published by them in 1981, titled: "Diffusion limited aggregation, a kinetic critical phenomena" in Physical Review Letters. number 47. Another more colourful description involves a city square surrounded by taverns. Drunks leave the taverns and stagger randomly around the square until they finally trip over one their insensate companions at which time, lulled by the sounds of peaceful snoring, they lie down and fall asleep. The tendril like structure is an aerial view of the sleeping crowd in the morning.
There are a number of ways of simulating this process by computer,
perhaps the most common is to start with a white image except for
a single black pixel in the center. New points are introduced at the
borders and randomly (approximation of Brownian motion) walk until
they are close enough to stick to
an existing black pixel. A typical example of this is shown below
in figure 1. If a point, during its random walk, approaches an edge
of the image there are two strategies. The point either bounces off
the edge or the image is toroidally bound (a point moving off the
left edge enters on the right, a point moving off the right edge enters
on the left, similarly for top and bottom). In general new points
can be seeded anywhere in the image area, not just around the border
without any significant visual difference. 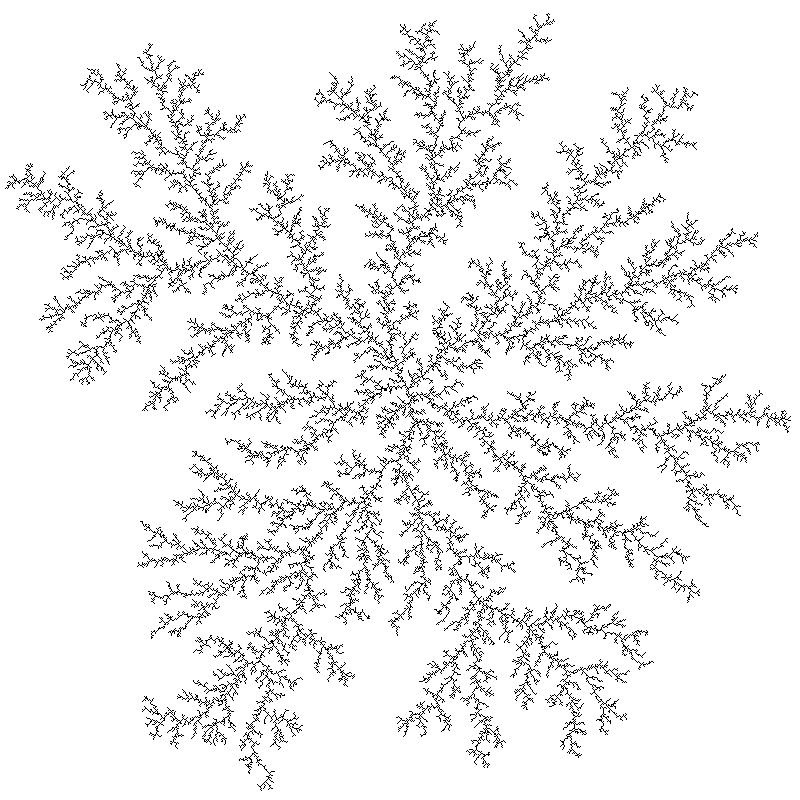 Figure 1. Point attractor
Another attractor geometry is a line, see figure 2. In this case the
bottom row of pixels are initially black and new points enter from the
top. The image is normally horizontally circular, that is, points move
off the left appear on the right and visa-versa.  Figure 2. Line attractor
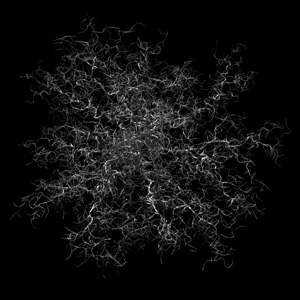
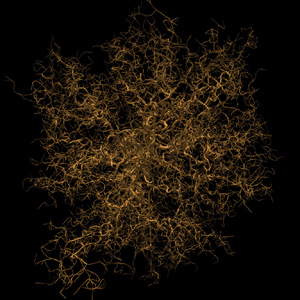
Figure 3 shows a box attractor, new points enter in the interior (the
center of the image say).
The source code supplied here generates the forms by a rather brute force
method which is hardly the most efficient. A common efficiency measure is
to start the new particles within a certain range of the current structure
and abandon them if they move outside some other range.  Figure 3. Rectangle attractor
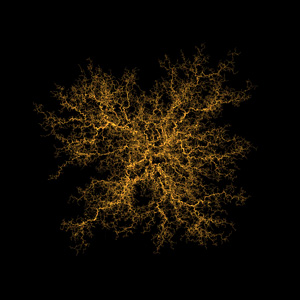
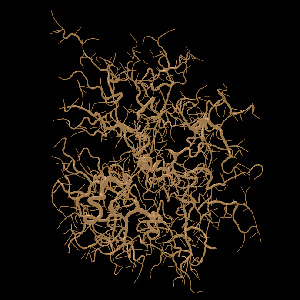
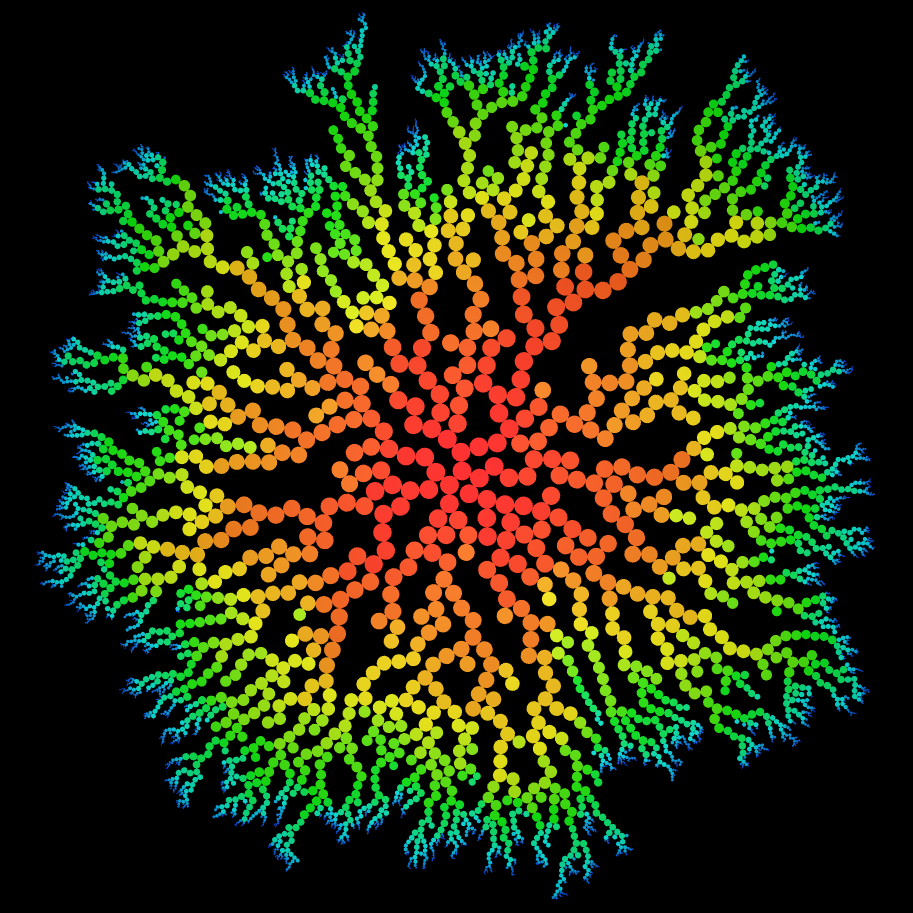
There are a number of ways of adding colour, figure 4 has a circular
seed region (toroidal bounds) and the particles are coloured by the
order in which they were introduced. 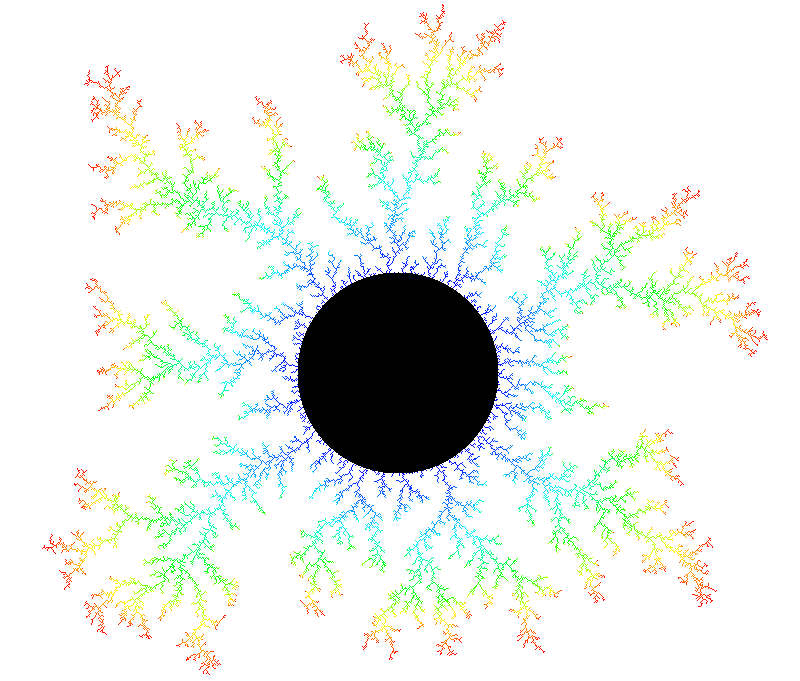 Figure 4. Circular attractor
 Figure 5. Internal circular attractor
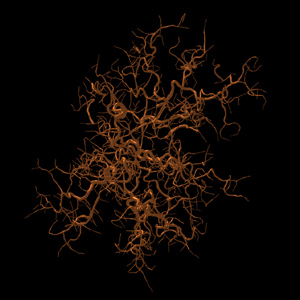
Another variation is to vary the so called "stickiness". In all the above example if the wandering particle struck part of the existing structure it always stuck (stickiness = 1). This can be modified by introducing a probability of sticking, the general result is to make the form more hairy and solid. 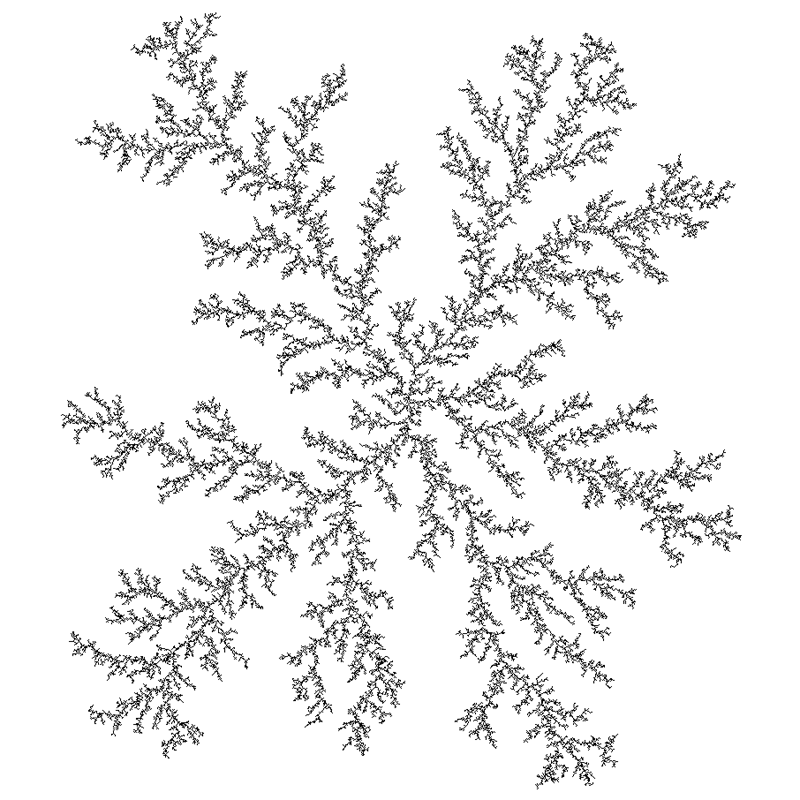 Figure 6. Stickines = 0.2
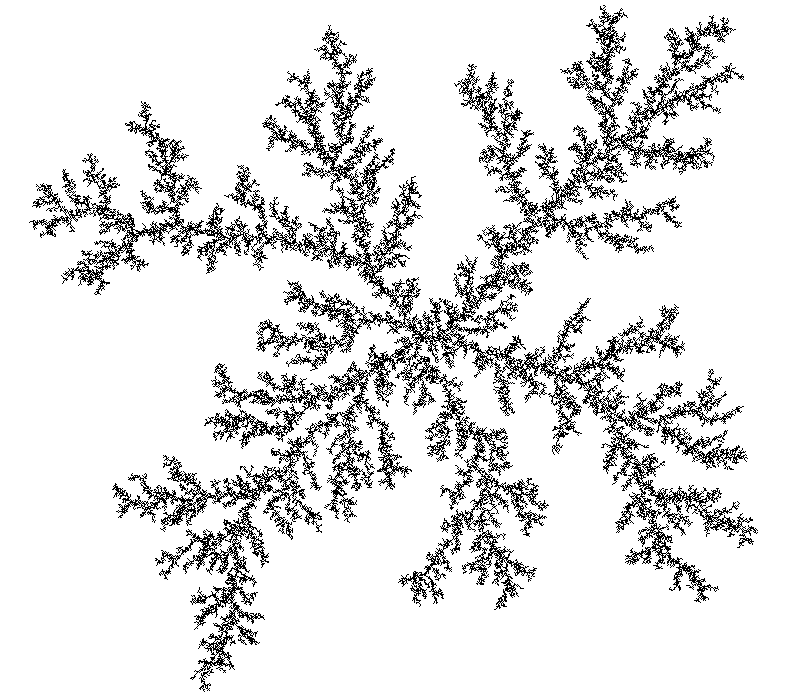 Figure 7. Stickines = 0.05
 Figure 8. Stickines = 0.01
 Frosty Windshield in the Morning Woods, Martha's Vineyard. Courtesy: Stephen Klebs Using spheres of decreasing radius



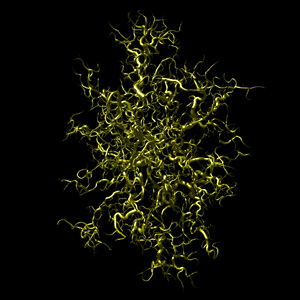
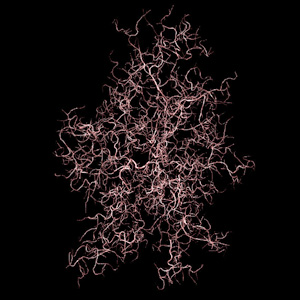
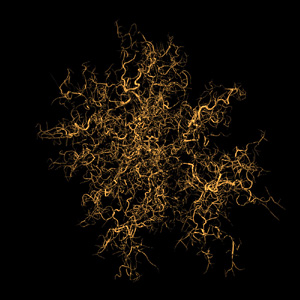
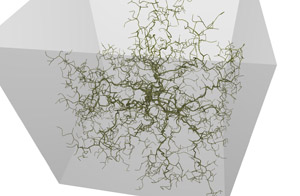
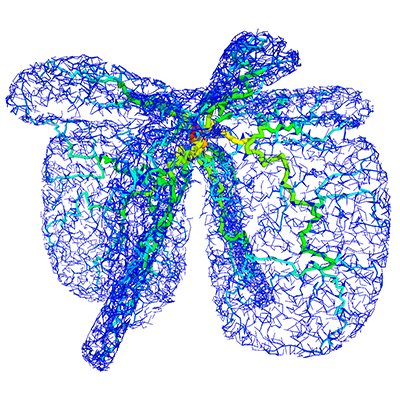
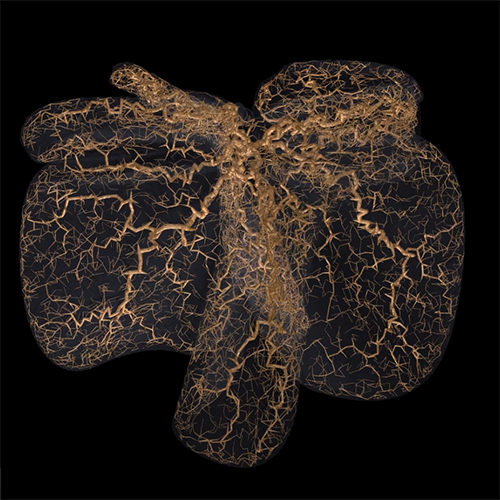
The following are examples of growth in three dimensions based upon the same
principles as diffusion limited aggregation, normally performed in
two dimensions. The basic principle involves a particle
that moves around randomly until it gets close to part of the existing
structure, at which point it sticks and becomes part of the structure.
The process is started with a seeding structure, normally a single point, and
continues until the structure reaches a desired size.
Exhibited at Museum of Design, Zurich. einfach komplex – Bildbäume und Baumbilder in der Wissenschaft. Simply Complex -- Picture-Trees and Tree Pictures in Science. 30 April 2005 -- 4 September 2005
The renderings here are created using POV-Ray, each particle is actually represented as a cone and a piecewise Bezier curve is used to smooth continuous chains of particles. As particles are added the thickness of the branch leading to that particle in thickened.
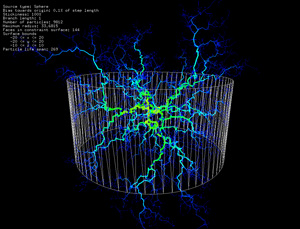
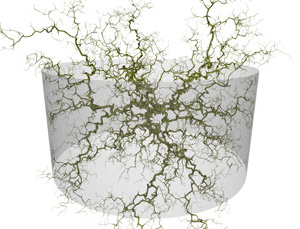
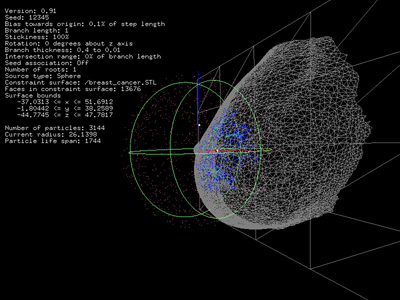
A further extension is to constrain the DLA growth to some "vessel". In the following the constraint takes the form a box (left) or cylinder (right) with one end open.
Grown over a sphere (planetarium), left: looking from inside the planetarium, right: from the outside of the dome.
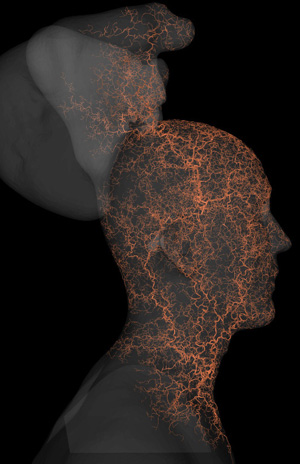
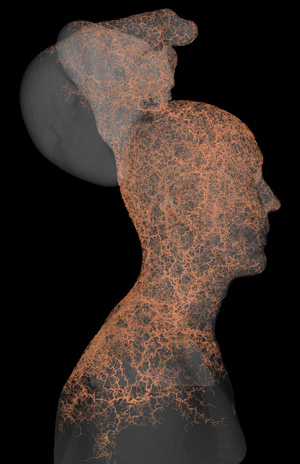
DLA grown within a 3D scanned model of the human head (plus antlers), described by a STL file. Part of modelling exercise for Philippe Vranjes.
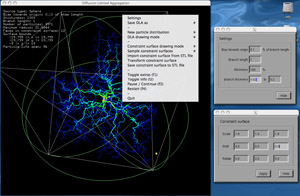
Software
The software presented here is made available for Mac OS-X, for Mac OS-X X-Windows must be installed and running. DLA structures can be grown in 3D, constraint surfaces applied, and resulting structures saved in PovRay format for high quality rendering.
Command line usage
> dla3dviewer -h
Usage: dla3dviewer [command line options]
Command line options
-h this text
-f full screen
-s active (quad buffer) stereo
-ss dual screen stereo
Mouse controls
left rotate camera
middle roll camera
right menus
Function keys: see menus
Keyboard commands
q quit
h reset camera
[,] roll camera
<,> more camera forward, backward
+,- zoom camera in, out
w window dump to TGA file
Growth inside a cup by David Sutton
Physical 3D printed realisations 
Simulation in a breast as a model for breast cancer
Project by Michael Eden, building DLA structure within Architectural elements. 
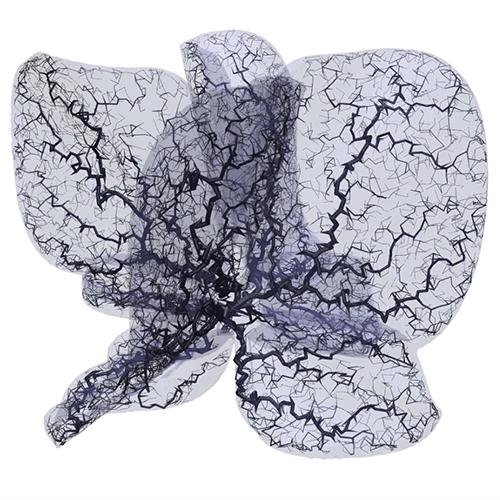
Project with Julie Muyldermans Growth within petal constraint volume.
Movies.
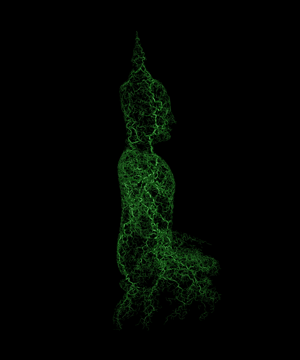
Grown within a Buddha statue (author)
Further examples 
Constrained Diffusion Limited Aggregation in 3 DimensionsPaul BourkePoster: Graphite (ACM Siggraph), Dunedin November/December 2005 See also: Computer and Graphics, Volume 30, Issue 4
Abstract Diffusion Limited Aggregation (DLA) has usually been studied in 2 dimensions as a model of fractal growth processes such as branching, lightning, snowflakes, mineral deposits, and coral. Here, the basic principles are extended into 3 dimensions and used to create believable models of root systems. A straightforward approach is introduced for constraining the growth of the 3 dimensional DLA by a surface or containing it within a vessel. PDF version: dla3d.pdf
Miscellaneous images
DLA in 3 Dimensions, volumetricThe standard 2D DLA can be most simply extended into 3 dimensions by using a 3D pixel grid, more commonly known as a voxel grid. During the random walk, indead of just 8 possible new positions (2D) there are now 26 possible new direction for the particle to move at each step of the random walk. 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||