Square FisheyeWritten by Paul BourkeSpecial tanks to Nan Ma for solving the inverse mapping equations See relationship to the Apple Pro headset (2024); January 2015
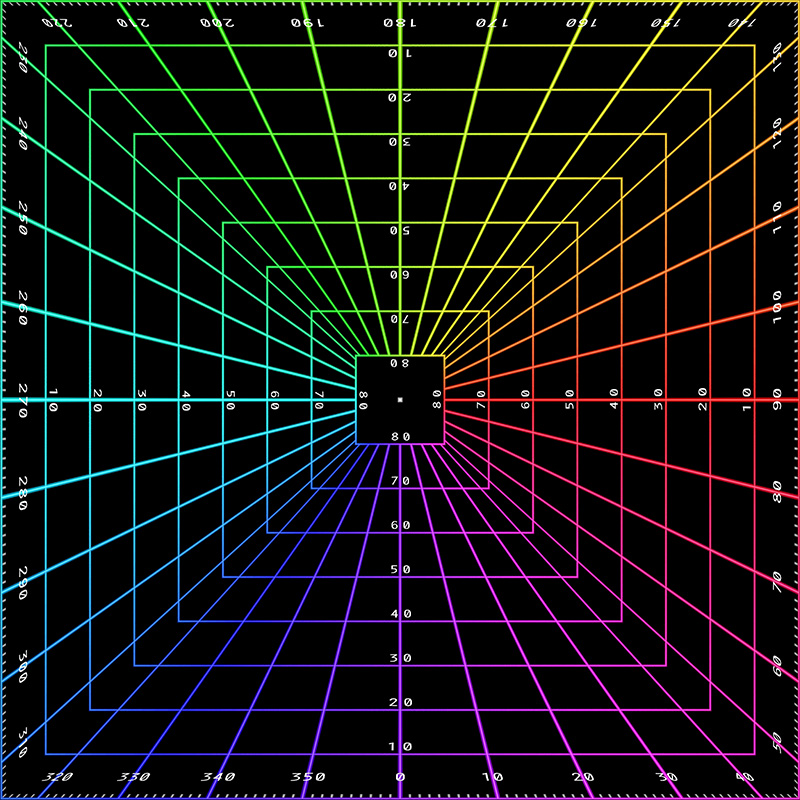
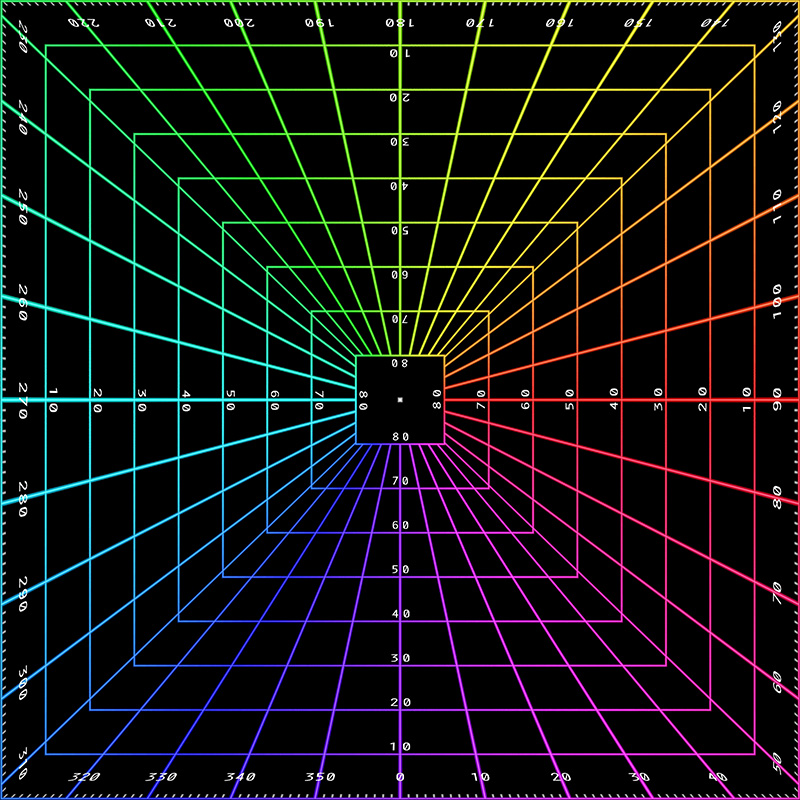
The following introduces the concept of a 180 degree fisheye (although other angles are possible) that fills a square image, rather than being limited to an inscribed circle as per the usual fisheye projection. The method presented here is just one of a large number of ways a circle can be expanded to fill a square. In the transformation here the field angle p(x,y,z) for every point (u,v) in a square image plane is given below. This mapping is conformal except for the 4 corner points of the square, that is, angles between features in the input image are preserved in the output image. The mapping is not equal area.
A 180 degree fisheye is represented in the traditional way in the first image below, the equivalent square fisheye is shown in the second image. For reasons that are not at all obvious, the MandelBulb3D software offers this as one of the rendering options, specifically, the "common" camera with 180 field of view. 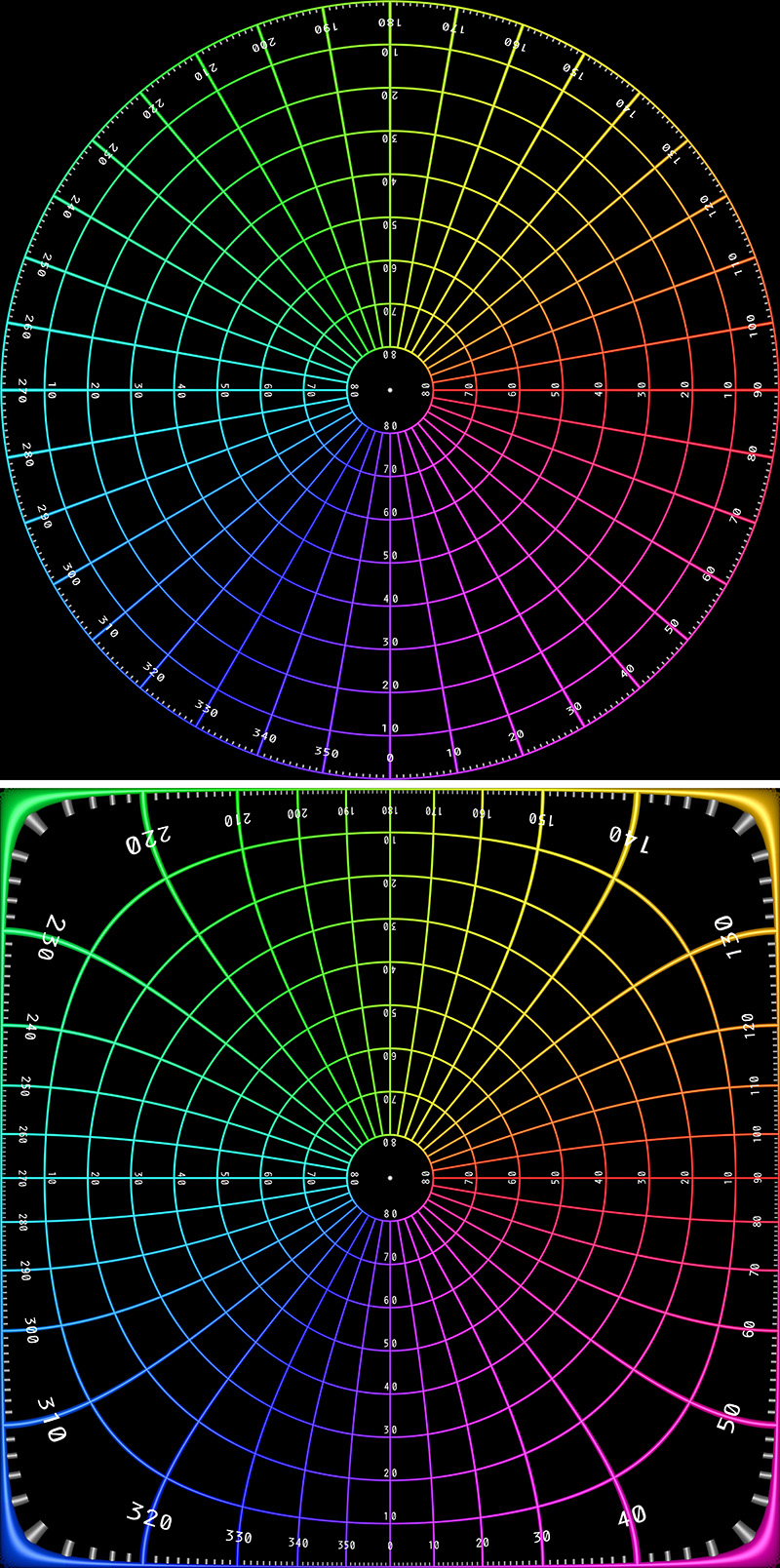
This projection has been discussed in papers by Chamberlain Fong under the somewhat more complex formulation called Schwarz-Christoffel mapping, credited to Hermann Schwarz and Elwin Christoffel. Unfortunately it uses complex analysis and the formulation uses rather complicated complex valued incomplete Legendre elliptic integrals of the 1st kind as well as complex valued Jacobi elliptic functions. The forward mapping can be expressed as a transformation from a 2D point on the image plane (u,v) to a unit vector p(x,y,z). Conversions between a circular fisheye image and square fisheye image is implemented as follows. 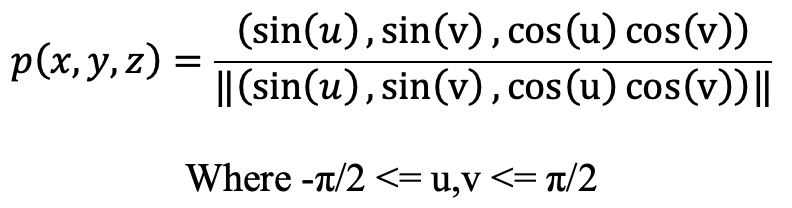
Where p(x,y,z) is the field angle for a particular pixel (u,v). The inverse mapping, solved by Nan Ma, is given below. Specifically, given a unit vector (x,y,z) what is the corresponding (u,v). Define the following 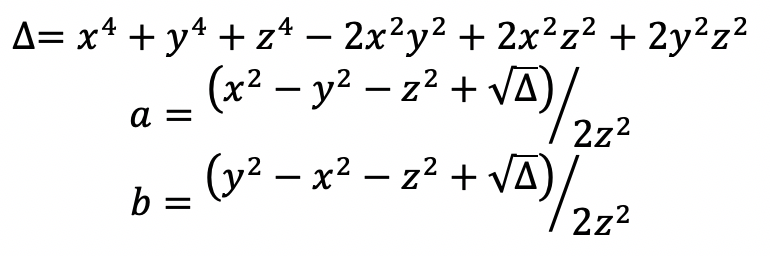
then
The forward and reverse mappings have been implemented in a command line style utility that can convert to and from standard circular fisheyes and square fisheyes. Please note that in this case the solution assumes the mappings are between vectors p(x,y,z) encoded as fisheye projections on the image plane. Usage: square2fish [options] squareimage Options -w n width and height of the fisheye image, default: 2048 -t n fisheye FOV (degrees), default = 180 -a n antialiasing level, default: 2 -o s output file name, default: name derived from input filename -d n direction, 1 or -1, default: 1 -v debug mode, default: off Examples from Mosque domes in New Delhi
2D, circle to square
In 2 dimensions one can map a circle to a square and the inverse (square to a circle) in a number of ways, the forward and reverse mapping for one possibility is given below. In the following the source image has normalised (-1 to 1) coordinates (u,v), the normalised coordinates of the destination image are (x,y). f(x,y) will be denoted as the forward transform and f'(x,y) the reverse. The following is known as the elliptical mapping and credited to Philip Nowell. 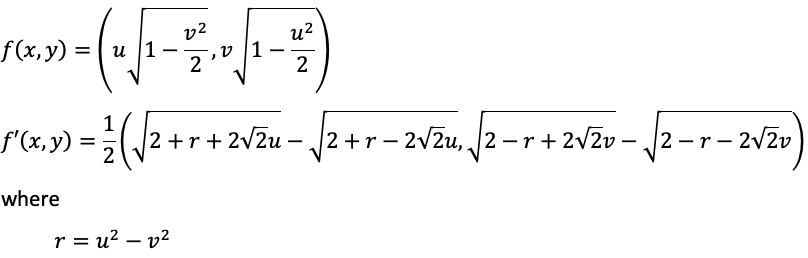
Using the same source polar fisheye image above, the mapping from a circle to a square is shown as follows. 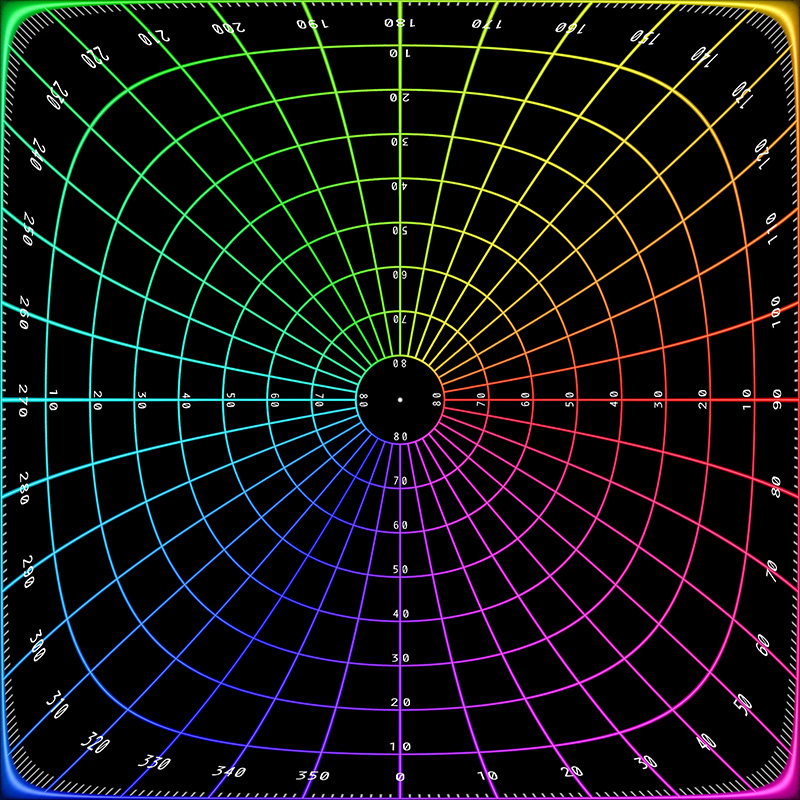
There are some other documented mappings, the circle to square is shown below but the inverses have also been derived. It should be noted that these are all different to the fisheye to square mapping introduced at the start of this document.
Usage: square2disc [options] squareimage
Options
-w n width and height of the output image, default: 2048
-m n method to use: 0 -> 5, default: 0
0 - Stretch
1 - Concentric
2 - Squircle
3 - Equal area v1
4 - Equal area v2
5 - Elliptical
-d n direction, 1 or -1, default: 1
-a n antialiasing level, default: 2
-o s output file name, default: name derived from input filename
-v debug mode, default: off
Stretch mapping. This is perhaps the simplest, one adjusts the radius of each point on the circle keeping the angle the same. 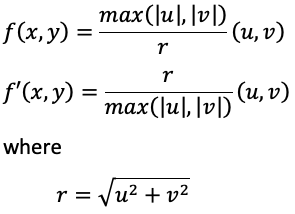
For some as yet unknown reason, Apple has chosen this as their, as yet undocumented, fisheye format for the Apple Vision Pro headset. An example shown below noting the horizontal axis is additionally rotated by 45 degrees. It's very hard to imagine any benefits to doing it this way since the headset needs to "undo" this image in order to present a wide angle projection to the viewer. Note that at the time of writing and given a scarity of examples, they could be using the concentric mapping below.
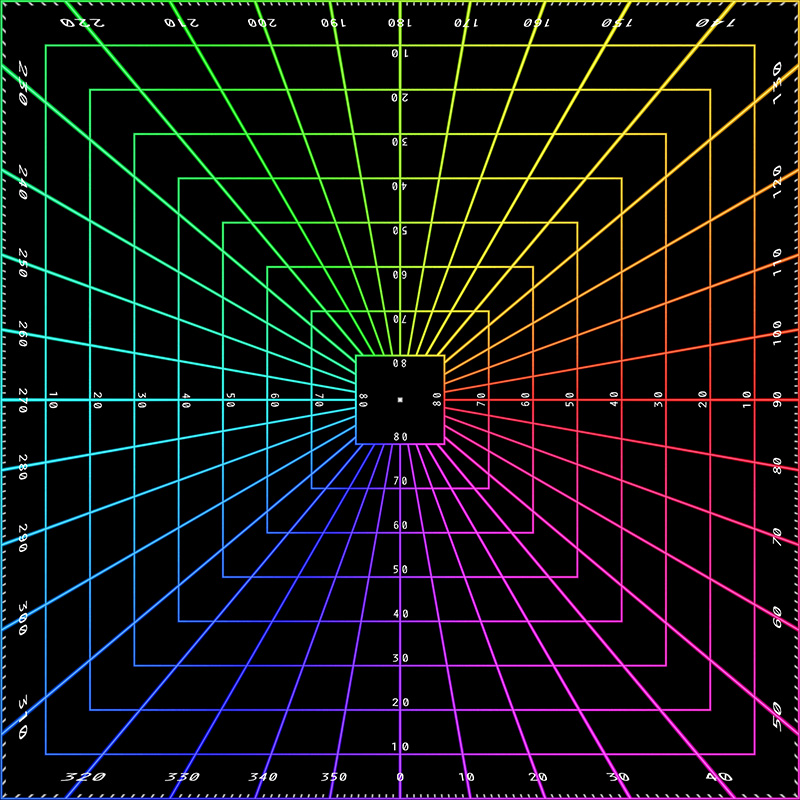
Concentric. This is also known as Shirley mapping, and credited to Peter Shirley and Kenneth Chiu. 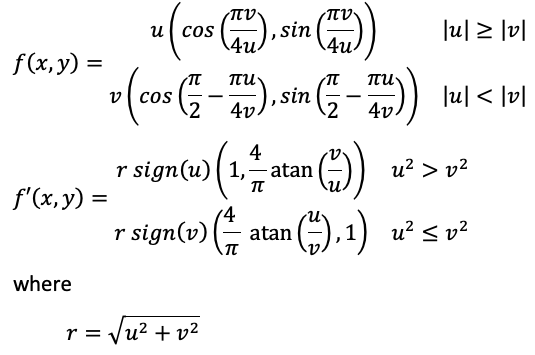
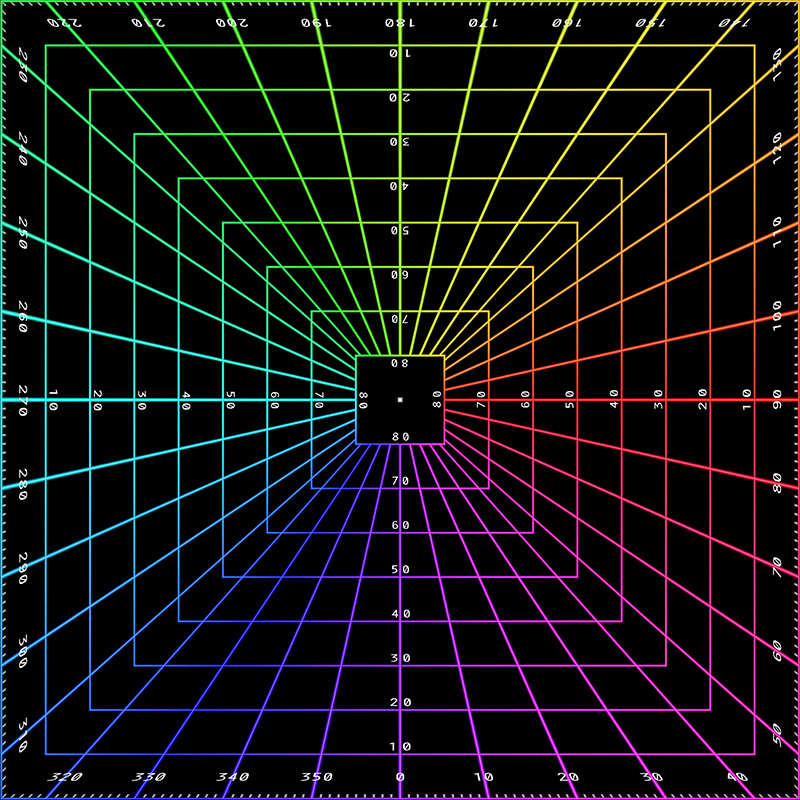
Squircle mapping. Credited to Fernandez-Guasti. 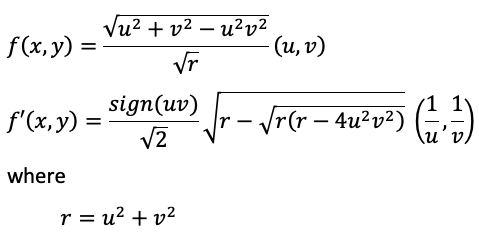
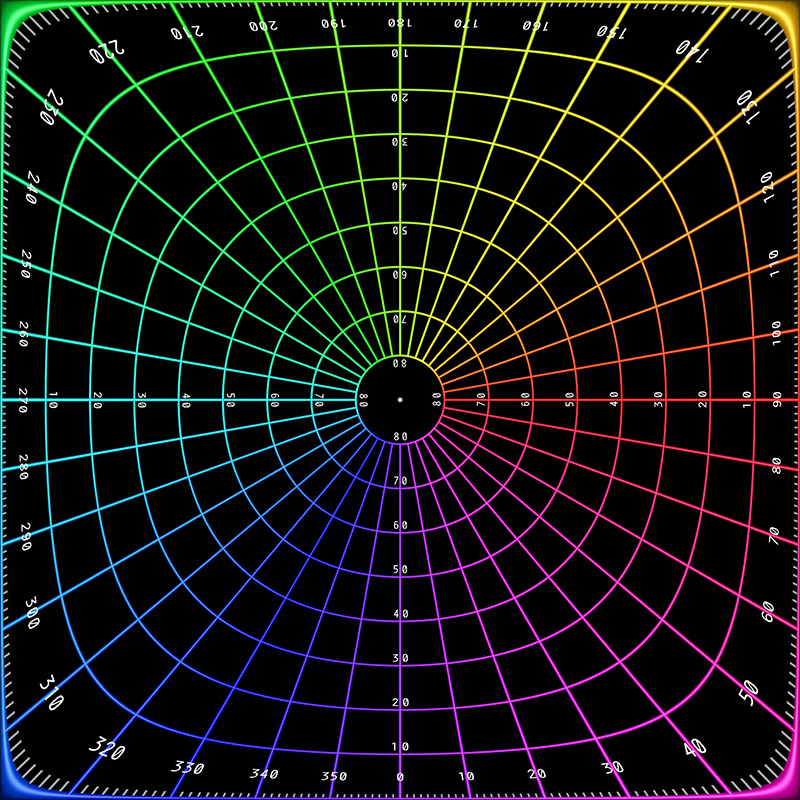
Equal area option 1. 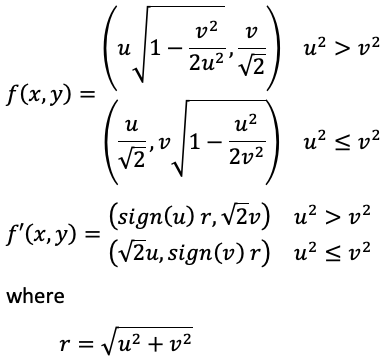
Equal area option 2. 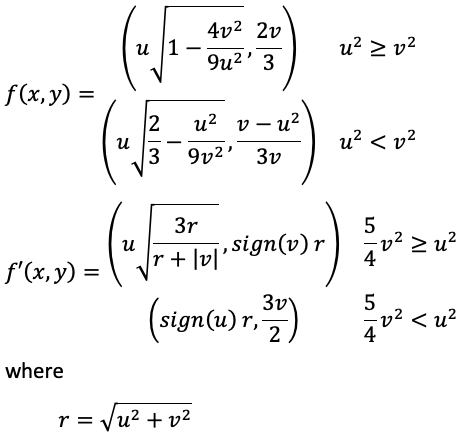
References
|





