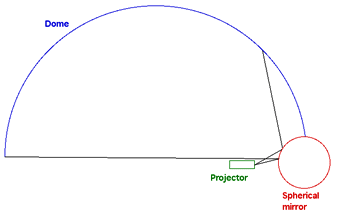
In this document I discussed a low cost system for projecting into planetarium domes using a single projector and a spherical mirror. The approach taken in that document is that content creators would render to fisheye images which would in turn be warped to create the correct views for the spherical mirror projection. This warping can be performed off-line or built into the movie playback software, (warping on the fly). Here an alternative direct rendering method is introduced, the correct warped image is created directly from the rendering (generally raytracing) process by simulating the projection geometry.

The general principle is straightforward, the dome projection consists of a projector and a spherical mirror, the projector is replaced with a matching virtual camera in a rendering software thus creating the correct image. Care needs to be taken to replicate the projection environment accurately, for example, using the correct radius mirror, using the same aperture on the camera as the aperture of the projector, etc. One unfortunate characteristic of data projectors is they usually project off-axis and raytracing packages don't always support that. This can be compensated for by rendering with a larger on-axis frustum and trimming the result.

As an example consider the rendering on the right, the scene just consists of a coloured polar grid located above the horizon (there is no geometry below the horizon). The camera is pointing at a mirror with the same zoom and position as the projector that will eventually project this image into the planetarium. The final image will have the bottom half trimmed away to replicate the exact off-axis frustum used by the projector.

Note the discontinuity in the sky In the above example, this is because the eventual projector frustum extends past the bounds of the mirror, likewise the rays from the rendering program miss the spherical mirror. This can be readily removed by adding a blocking plane at the appropriate depth on the mirror. Normally the mirror ball will interact with the scene, cast shadows, etc. Some rendering application can turn shadow casting off on an object-by-object basis. When this isn't supported the solution is to make the sphere microscopically small but still place it proportionally closer to the camera and hope (plan) that it doesn't come between the camera and a light source say.

One use of the mirror dome projection is as a preview environment for people who are working on dome content but who don't have access to a preview environment. Instead of rendering fisheye views (generally more expensive) and then warping those, this approach allows a fast direct test rendering process. In general it is recommended that high resolution fisheye images are created since they can be warped into many different mirror projection environments. The process discussed here is targeted at creating images for fast viewing or for content only destined for a single environment.

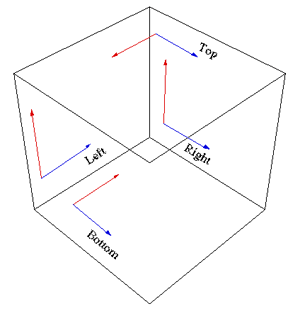
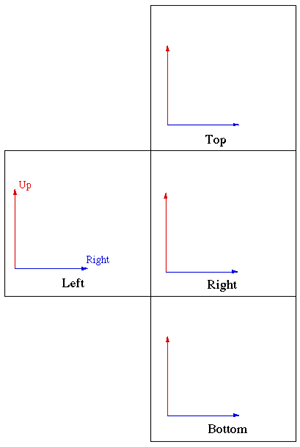
Introduction

There are a number of techniques that can be employed to render content for non standard displays such as domes. Only in rare cases does the rendering software support direct rendering that will take into account the necessary distortion of the projector and projection surface. In other cases one needs to create the correctly distorted image from simple perspective or orthographic projections supplied in all rendering packages. This document will describe one method that is rather sneaky and will work with "any" package although it does suffer from some problems.

The technique involves creating a mirror or lens as a geometric primitive that is placed in front of a camera. The mirror is designed precisely so that the captured image, when projected, will look correct on the intended projection screen.

Before considering the mirror method it should be pointed out that there are other ways of creating such content. One very popular method is to render a 4, 5, or 6, 90 degree perspective views along each orthogonal axis forming a cube (otherwise known as an environment map). This has been discussed here and applied to creating content for planetariums here. The basic setup of the cube is shown below. Some people choose to render 4 faces, most people choose 5 because the bottom half of the 4 surrounding faces can more easily be excluded from the rendering.

An example rendering in the format of the unfolded cube is shown below on the left. The image ready for projection in the dome is shown on the right. Note that a full dome image can be created from the cube but in the case of the some systems (Elumens VisionStation) the bottom quarter is not used.

Mirror method

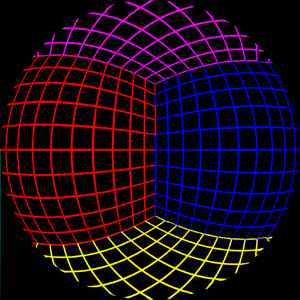
As mentioned, the basic approach is to design a mirror and capture the image reflected from it. The basic setup is shown below, the "final camera" is the one being used with the mirror, the "test camera" is used for testing purposes, it may be a wide angle or angular fisheye if that is supported. Of course the magic is in the design of the mirror which creates an image so that when projected through the hardware gives the correct view. In this case the lens has been calculated so as to work with an orthographic (parallel) projection.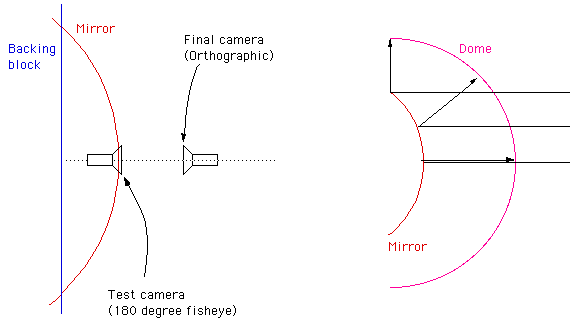

The test scene rendered as a fisheye and with the mirror is given below. The differences are not great and mostly occur in the mid regions, essentially the difference between a linear ramp and a sinusoid.

Mirror

180 degree fisheye

The PovRay source code for the above images can be found here. The file "lens.inc" contains the mesh triangle primitives describing the lens, this includes vertex normals to give a smooth surface without an excessive number of polygons. The back of the mirror is placed at x=0 and it lies in the y-z plane, it extends to about 0.4 at the thickest along the x axis.
The file "camera.pov" sets up either a preview or a mirror reflecting camera. It expects four variables to be defined in the scene file, they specify the camera position (VP), direction (VD), up vector (VU), and camera type (MODE). The mode specifies either the mirror camera (0) or a fisheye camera (1). The camera orientation variables are used to reposition the mirror in the correct place in front of the camera using a matrix transformation on the mirror geometry.

   scale <SCALEFACTOR,SCALEFACTOR,SCALEFACTOR>
   translate <-0.41,0,0>
   matrix <UVD.x, UVD.y, UVD.z,
           UVR.x, UVR.y, UVR.z,
           UVU.x, UVU.y, UVU.z,
           VP.x,  VP.y,  VP.z>

For an example on how to use these files see "testscene.pov", the scene geometry for this was created using "makescene.c". Note that the mirror is a circular object and a black backing sheet is placed behind it to obscure any scene geometry around the edges. So while the mirror is perfectly reflective, the blocking sheet is perfectly black and absorbing.

Mirror

180 degree fisheye

Issues

There are a number of issues/problems relating to this technique.

• It can of course be rather messy, whichever method is used to implement the mirror and keep it aligned with the camera has to be written carefully.

• Since the lens is now part of the world geometry it may interact with the environment in some way, for example it may cast a shadow. This can be reduced to an unlikely event by making the mirror very tiny, see the SCALEFACTOR variable in the PovRay source provided.

• It is also possible that some other scene geometry may get between the camera and the mirror. While it is usually bad form to get the camera so close to solid material (especially for a very small mirror) it is less uncommon when using environmental effects such as fog. The times when this is a problem is quite rare, usually the camera is supposed to be in the fog anyway.

• In the case of the Elumens VisionStation the above is not perfect. The viewer is not located in the center of the dome, nor is the projector in the center. To create a correct projection a so called offaxis projection is required. While this is straightforward for the cube approach, it isn't readily possible for the mirror approach.