Graphical exploration of the connectivity sets of alternated Julia sets; M, the set of disconnected alternated Julia setsNon-linear Dynamics, Springer, March 2013. DOI: 10.1007/s11071-013-0859-yM.F. Danca1,2, P.D. Bourke3, M. Romera4
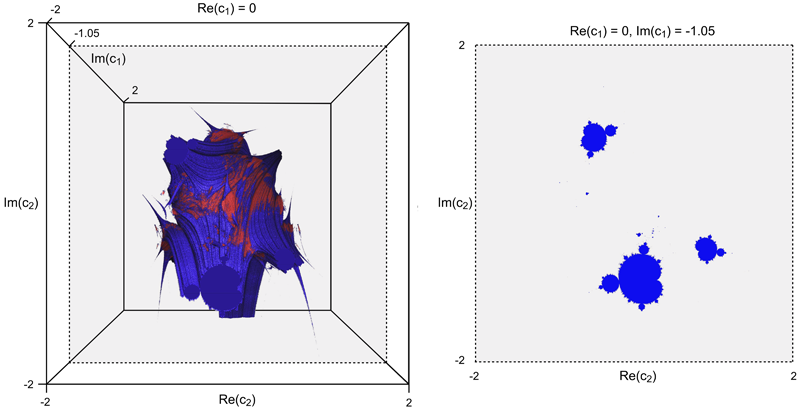
[1] Dept. of Mathematics and Computer Science, Avram Iancu University, 400380 Cluj-Napoca, Romania Abstract Using computer graphics and visualization algorithms, we extend in this work the results obtained analytically in [1], on the connectivity domains of alternated Julia sets, defined by switching the dynamics of two quadratic Julia sets. As proved in [1], the alternated Julia sets exhibit, as for polynomials of degree greater than two, the disconnectivity property in addition to the known dichotomy property (connectedness and totally disconnectedness) which characterizes the standard Julia sets. Via experimental mathematics, we unveil these connectivity domains which are four dimensional fractals. The computer graphics results show here, without substituting the proof but serving as a research guide, that for the alternated Julia sets, the Mandelbrot set consists of the set of all parameter values, for which each alternated Julia set is not only connected, but also disconnected. Keywords: Alternated Julia sets; connectedness; quadratic maps.Preprint: preprint.pdf Figure 1
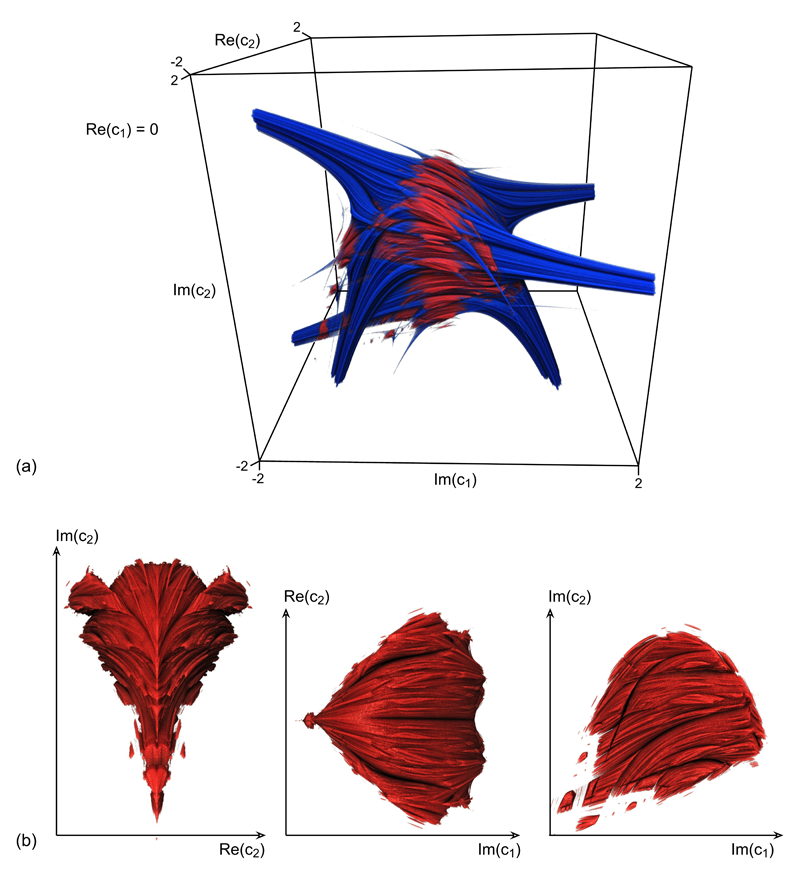 Figure 2
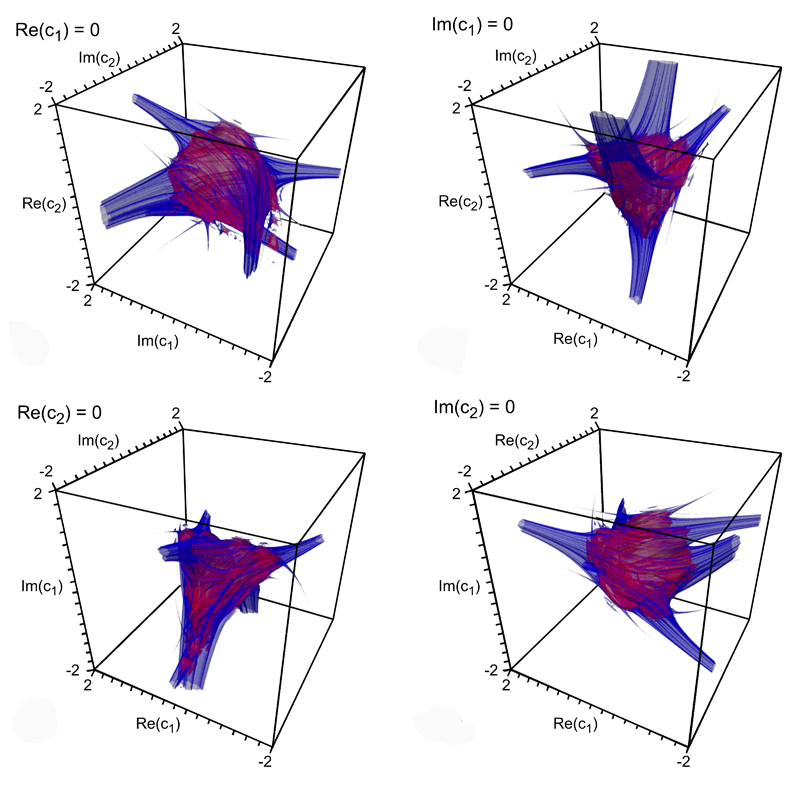 Figure 3
 Figure 4
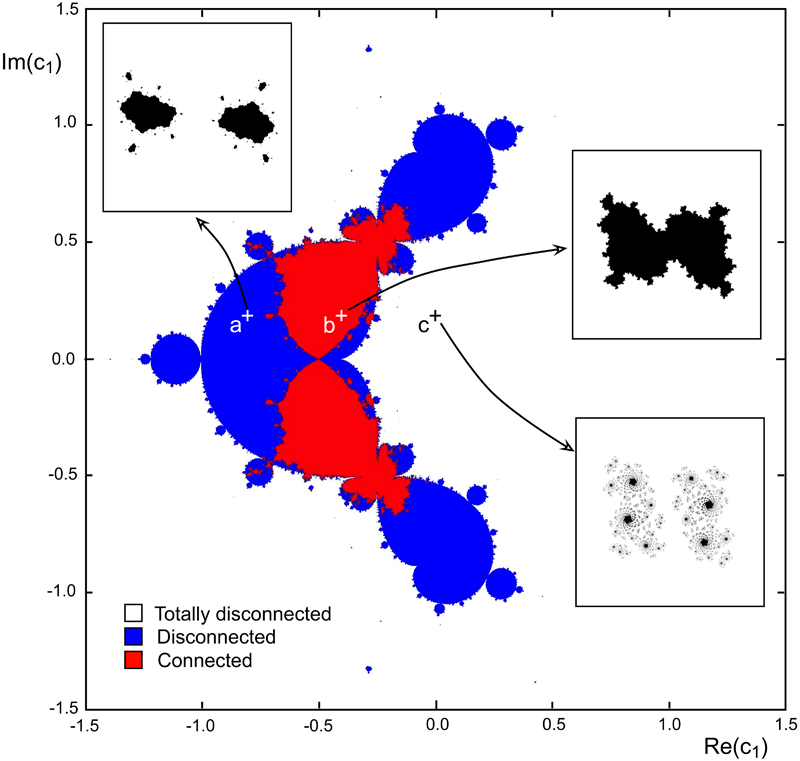 Figure 5
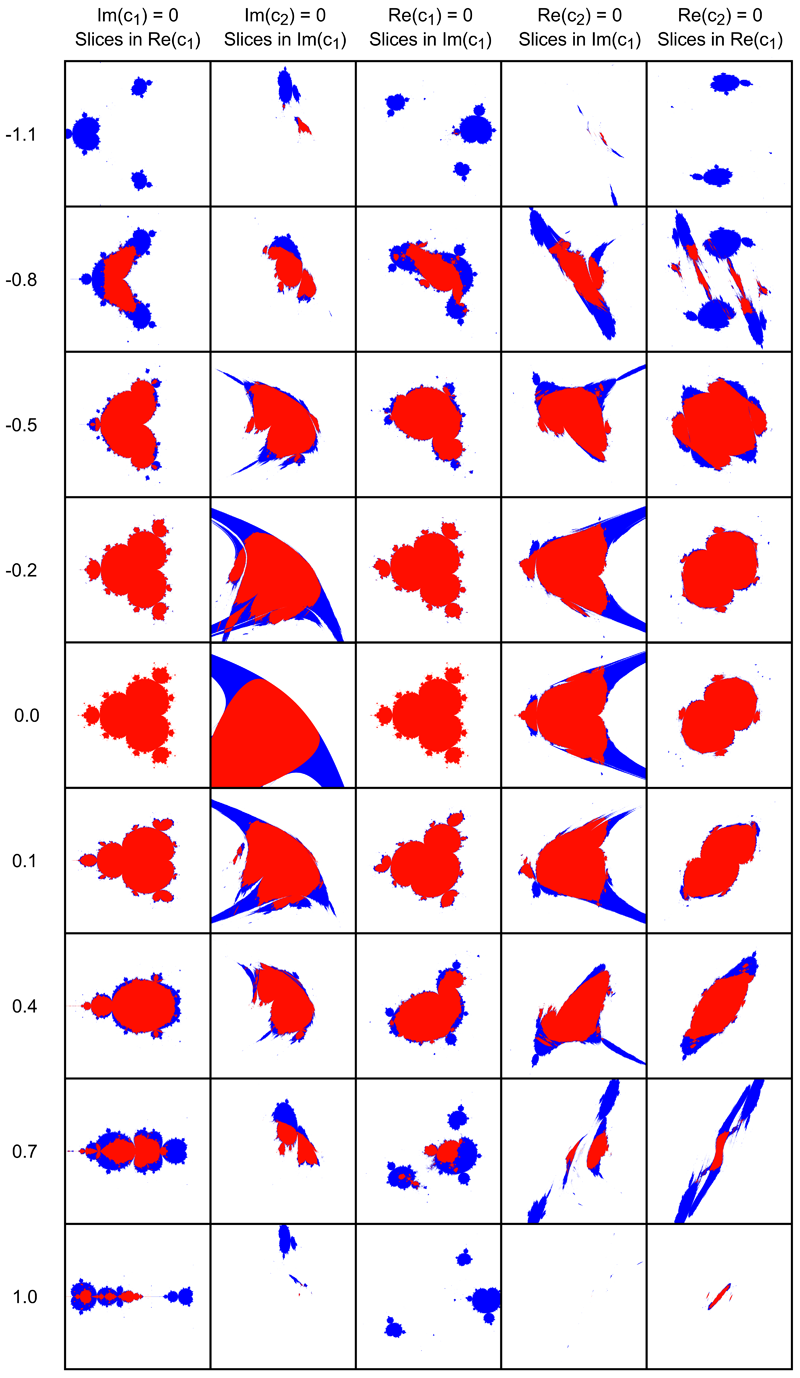 Figure 6
|