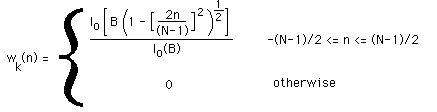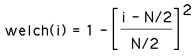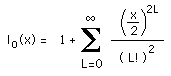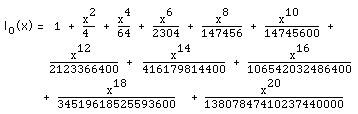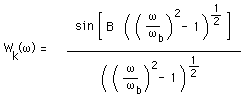Windows
Welch --
Bartlett --
Hanning/Hamming --
Kaiser
Written by Paul Bourke
August 1998
Welch
|
The Welch window for N points is defined as
where 0 <= i < N
|
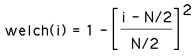
|
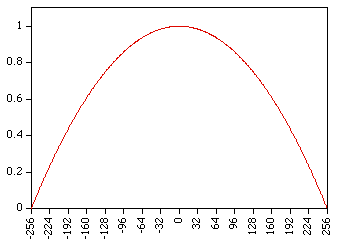
Centered around 0 this looks like
|
|
Commonly used as a window for power spectral estimation.
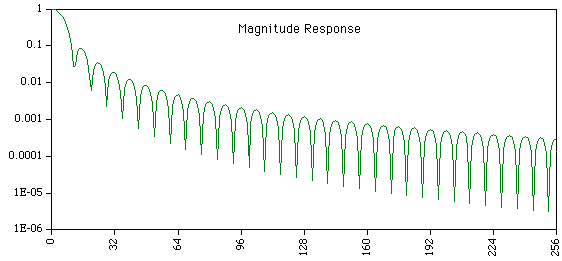
The magnitude response is
Bartlett window
|
Also known simply as the Triangular window
The Bartlett window of width N is defined as
|

|
The function is simply
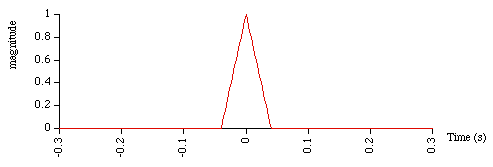
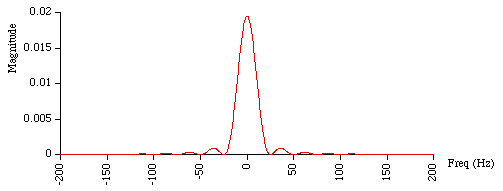
The frequency response is sinc2 (a triangle is the convolution
of two square windows so the convolution is the product of two sinc functions).
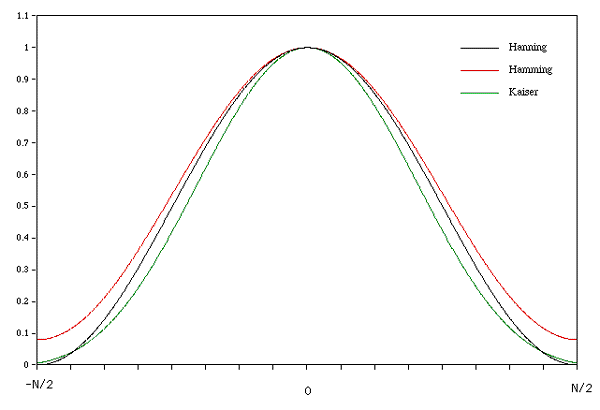
Hanning/Hamming window
|
Also known as the raised cosine window
The Hanning window for N points is defined as
where -N/2 <= i < N/2
|
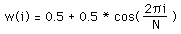
|
|
The Hamming window is
|
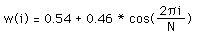
|
|
These are specific examples from a general family of curves of
the form
|
w(i) = a + (1 - a) cos(2 pi i / N)
|
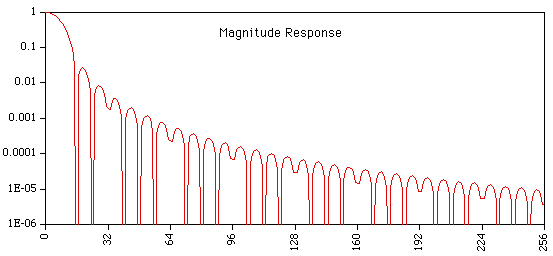
The magnitude response is
Shown below is the surface generated in Mathematica of the above
function varying the parameter "a".

Kaiser-Bessel window
The Kaiser or Kaiser-Bessel window is an approximation to a restricted
time duration function with minimum energy outside some specified band.
In the discrete case it is defined as
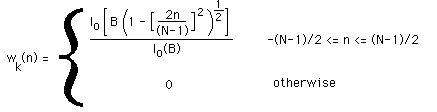
|
where N is the window width, B is half the time-bandwidth product. B
determines the trade-off between the magnitude of the side-lobes and the energy
in the main lobe and is often specified as a half integer multiple of pi.
Io is the zero order modified Bessel function of the first kind, a series
expansion of which is:
|
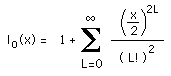
|
|
The expansion to 20 decimal places is
|
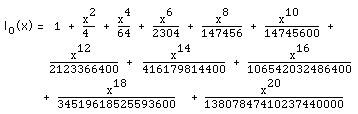
|
|
Analytic forms of the spectrum are not available but it can be shown that
the frequency spectrum in the continuous case is proportional to:
|
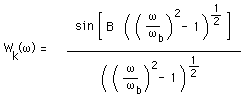
|
where wb is the width of the central lobe.
|
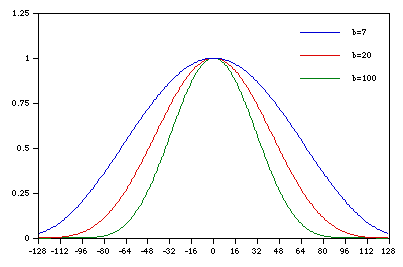
Example curves for different values of B
|
|
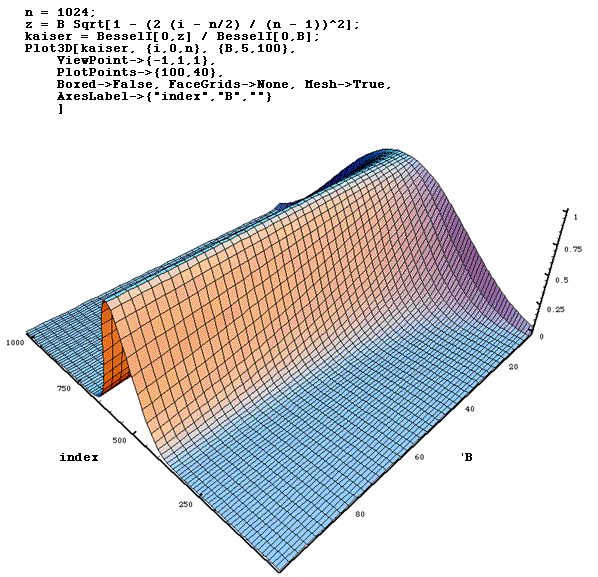
Using Mathematics a surface plot showing the window as a function
of B.
|