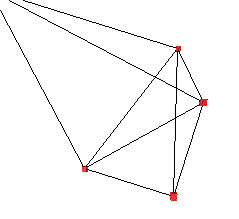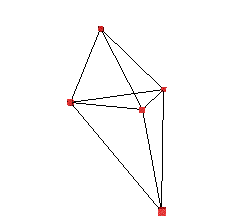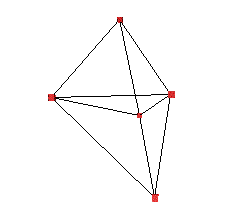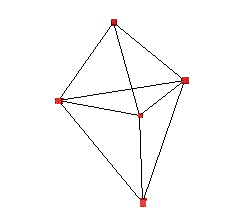
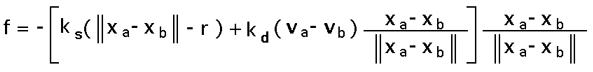Particle System ExampleSee also Solving systems defined by differential equations
Written by Paul Bourke
The following discusses the requirements of a simple "particle" system, that is, a collection of point masses in 3D space possibly connected together by springs and acted on by external forces. These particle/spring system will obey the laws of physics appropriate to such a configuration, the forces on the particles will include gravitation (optionally) and viscous drag (friction). The springs will exert forces on the particles according to Hooks law including spring damping. We are primarily interested in how the particles move given the forces acting on them, this is described by Newtonian mechanics, basically
where f is the force on a particle, m its mass, x its position, and a the acceleration. Note that f, x, and a are vectors in 3 space (x,y,z). The above second order system can be written as two first order differential equations making them easier to solve. a = dv / dt
There are two data structures required, one for the particles and one describing the springs. The structure for the particles includes their mass (normally constant) and the instantaneous position, velocity and force.
typedef struct {
double m; /* Mass */
XYZ p; /* Position */
XYZ v; /* Velocity */
XYZ f; /* Force */
} PARTICLE;
The structure for a spring includes the two particles it connects,
and various spring attributes required for the force calculation,
see later.
typedef struct {
int from; /* Particle "a" */
int to; /* Particle "b" */
double springconstant;
double dampingconstant;
double restlength;
} PARTICLESPRING;
The key to determining the dynamics of the system is calculating the forces acting on a particle given the current state of the whole system. Three forces will be considered here, they are
The particles might exert a gravitational attraction on each other. The gravitational attraction of one particle "a" due to another particle "b" is given by 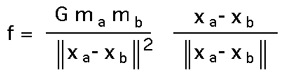
and is in the direction along the line joining the two particles. G is referred to as the universal gravitational constant and equals 6.672 x 10-11N m2 kg-2 The particles could have a charge, this very similar in form to the gravitational law except that now the particles may repel if the charges are the same sign and attract if they are the opposite sign. The exact relationship is given by Coulombs law 
Where k is known as Coulombs constant equal to 8.9875 x 109 N m2 C-2. As for the gravitational force the electrostatic force acts along the line defined by the positions of the two particles. Other forces can be added to this list dependent on requirements, it is only necessary to determine the appropriate physical forces involved.
C sourceThe algorithms needed to solve the differential equations are described in more detail in the link given in the title. The subroutines provided at the end of this discussion implement the Euler and midpoint algorithms but could easily be modified for any of the possible algorithms such as the Runge-Kutta. Generally, a simple solver is used because of the need to solve for a large number of particles and the derivative functions are relatively simple. The routines needed to implement the particle system described here are found in two files particlelib.h and particlelib.cThe basic program layout for a particle system implementation using the above routines is as follows
Create the particles
Create the springs between the particles
Initialise the particle and spring parameters
loop in time {
Update the particle positions (solve ODEs)
Display the results somehow
}
int main(int argc,char **argv)
{
int i,p1,p2;
double dt = 0.1;
InitialiseSystem();
while (TRUE) {
UpdateParticles(particles,nparticles,physical,springs,nsprings,dt,1);
for (i=0;i<nparticles;i++)
/* Display a particle at particles[i].p */
for (i=0;i<nsprings;i++) {
p1 = springs[i].from;
p2 = springs[i].to;
/* Display a spring between point p1 and p2 */
}
}
free(particles);
free(springs);
}
/*
Set up the particle system.
Initialise all variables to default values
*/
void SetupParticles(int np,int ns)
{
int i;
nparticles = np;
nsprings = ns;
if (particles != NULL)
free(particles);
particles = (PARTICLE *)malloc(nparticles * sizeof(PARTICLE));
if (springs != NULL)
free(springs);
springs = (PARTICLESPRING *)malloc(nsprings * sizeof(PARTICLESPRING));
for (i=0;i<np;i++) {
particles[i].m = 1;
particles[i].fixed = FALSE;
particles[i].v.x = 0;
particles[i].v.y = 0;
particles[i].v.z = 0;
}
for (i=0;i<ns;i++) {
springs[i].springconstant = 0.1;
springs[i].dampingconstant = 0.01;
springs[i].restlength = 5;
}
physical.gravitational = 0;
physical.viscousdrag = 0.1;
}
/*
Create 5 particles
The particles are placed randomly on the interval -5 -> 5
*/
void InitialiseSystem(void)
{
int i;
SetupParticles(5,9);
/* Random positions */
for (i=0;i<5;i++) {
particles[i].p.x = 10 * (rand() % 1000 - 500) /1000.0;
particles[i].p.y = 10 * (rand() % 1000 - 500) /1000.0;
particles[i].p.z = 10 * (rand() % 1000 - 500) /1000.0;
}
/* Edges */
springs[0].from = 0; springs[0].to = 1;
springs[1].from = 0; springs[1].to = 2;
springs[2].from = 0; springs[2].to = 3;
springs[3].from = 4; springs[3].to = 1;
springs[4].from = 4; springs[4].to = 2;
springs[5].from = 4; springs[5].to = 3;
springs[6].from = 1; springs[6].to = 2;
springs[7].from = 2; springs[7].to = 3;
springs[8].from = 3; springs[8].to = 1;
}
|