Mean and VarianceWritten by Paul BourkeJune 1991
There are many quantities that can be used to describe properties of a distribution. In what follows some of the more common quantities are briefly discussed and defined. The mean is a measure of the center or most likely value in a distribution. For N samples from some population, the mean (also sometimes called the average or expected value) is defined as 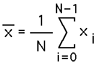
There are other quantities that also give a measure of the most likely value. The mode is the most often occurring value, generally only applicable for integer samples. The midrange is the middle value, that is, half the sum of the highest value plus the lowest value. The median is defined as the value that divides a population in two, half the observations are above the median and half below. The variance and standard deviation are a measure of the extent to which a distribution varies from its mean. The simplest measure of variation is the range, the difference between the largest and the smallest value, the variance however has more desirable features. The variance (square of the standard deviation) is defined as 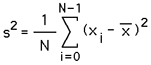
For computational ease the above is often expanded as follows to avoid the need to pre-calculate the mean. 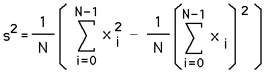
The standard error of the mean is defined as the standard deviation divided by the square root of the number of estimates.
Center of Mass and Radius of GyrationWritten by Paul BourkeMay 2004
Definitions for center of mass (also known as center of gravity) and radius of gyration for discrete points are given below. Center of Mass
Center of Gyration
The average square distance to the center of gravity.
|