Least SquaresWritten by Paul BourkeJune 1997
One often has a number of data points and the need to describe the behaviour of the data with a function of a known form. In general the data points are noisy samples and the functions parameters can't be chosen so as to exactly describe all the samples. The desire then is to find the parameters of the function that "best" describe the samples. The method of least squared error is one common choice of the "best" estimate. The squared error is the sum of the squared differences between each sample and the expected value as predicted by the function. The parameter values that minimise this error are considered the best estimates. The first example will illustrate the key points behind the technique by applying it to a problem that can readily be worked out manually. Example 1Consider finding the equation of a straight line given n samples (xi,yi). We will fit the function f(x) = ax + c, the normal definition of a linear function where a is the slope, and c is where the line intercepts the y axis. The key features and conventions are illustrated below. 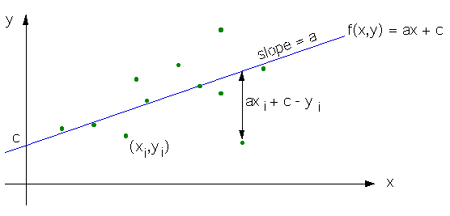
The general expression for the least square error E is defined as
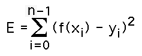
In this particular case it is 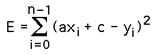
This function will have a minimum where the first derivatives with respect to a and c are 0. DE/dc = 0 = (ax0 + c - y0) + (ax1 + c - y1) + ... + (axn-1 + c - yn-1)
These can be rewritten as
a (x0 + x1 + ... + xn-1) + c (1 + 1 + ... + 1) = y0 + y1 + ... + yn-1
From the above it might be observed that if we define the vectors y = (y0, y1, y2, ... yn-1) u = (1,1,1,... 1)
then we can write the problem as two simultaneous equations with two unknowns, a and c as follows
a u.x + c u.u = u.y
Where "." refers to the vector dot product. Solving the above two equations for a and c is straightforward. In general all least squares estimates irrespective of the type of function or how many parameters can be formulated into an set of simultaneous equations. There are the same number of equations as there are unknowns or parameters to be fitted. Example 2To fit a plane f(x,y) = ax + by + c given samplesy = (y0, y1, y2, ... yn-1) z = (z0, z1, z2, ... zn-1) and applying the same derivation as in the case of the line we get 3 simultaneous equations and 3 unknowns
a y.x + b y.y + c y.u = y.z a u.x + b u.y + c u.u = u.z
These and larger sets of simultaneous equations can be readily solved using standard Gaussian elimination, see here for more details and source code. |