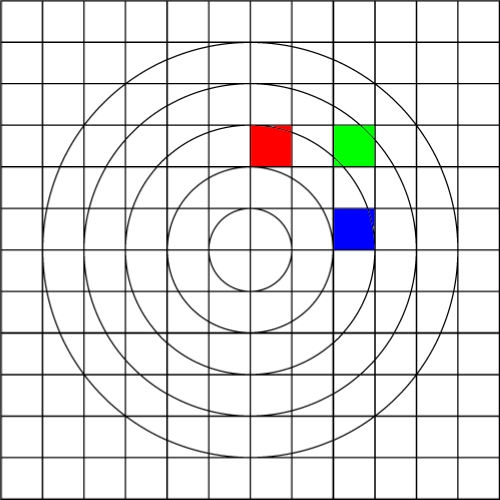
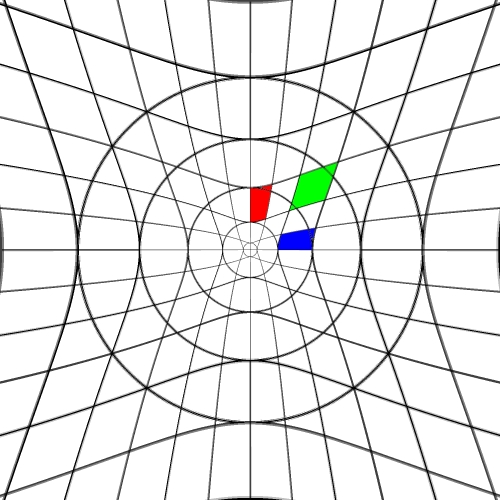
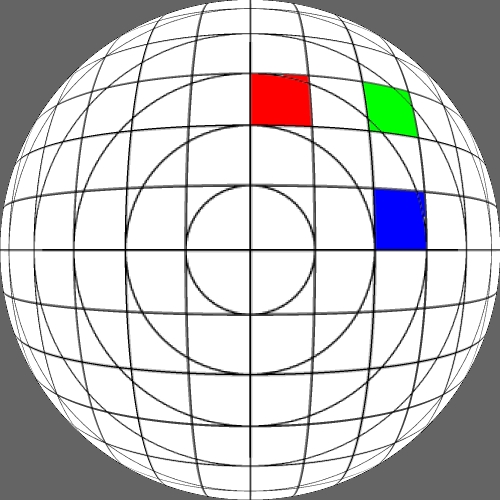
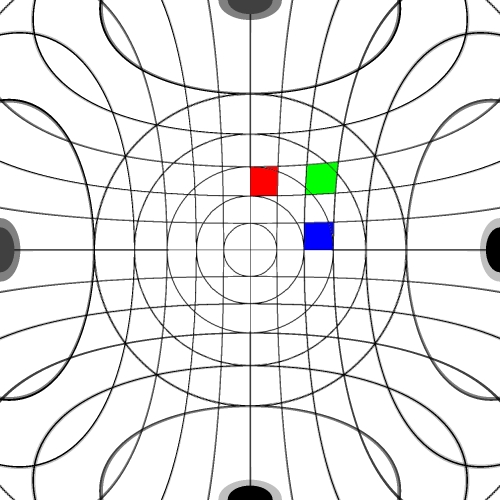
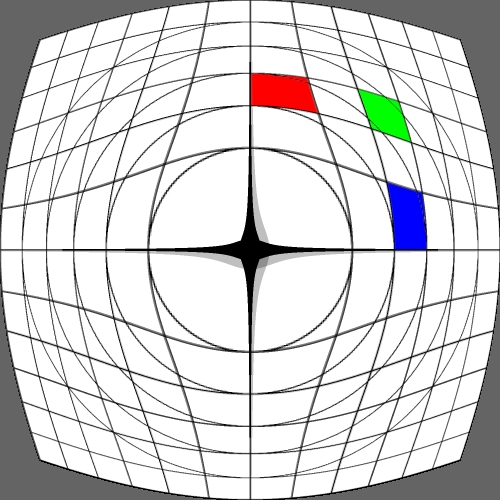
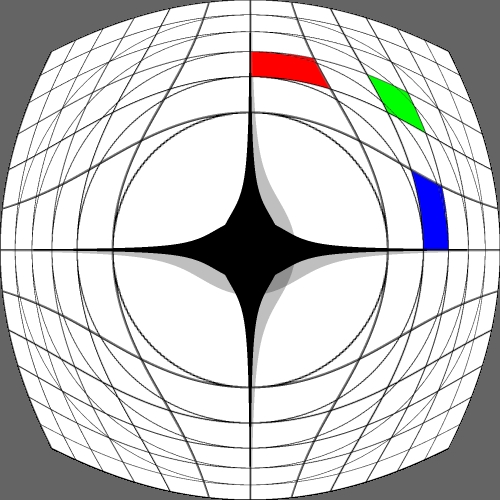
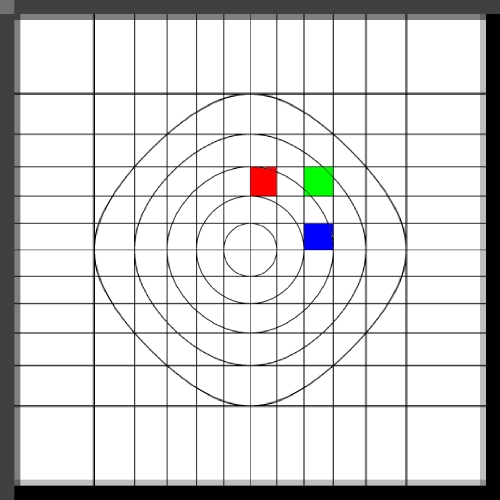
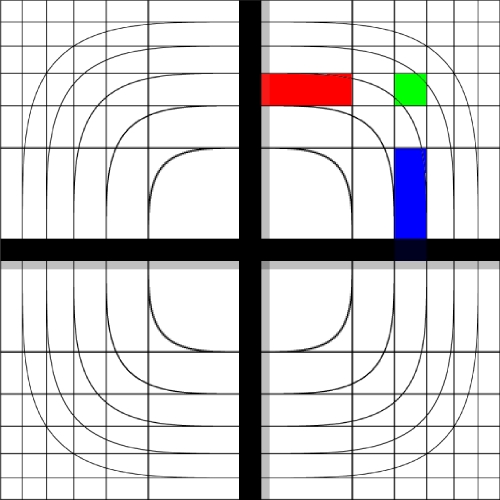
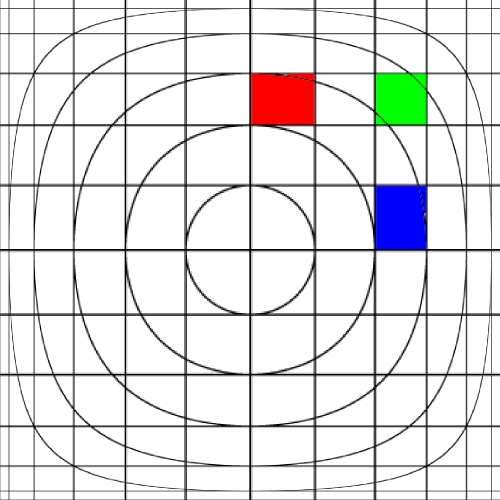
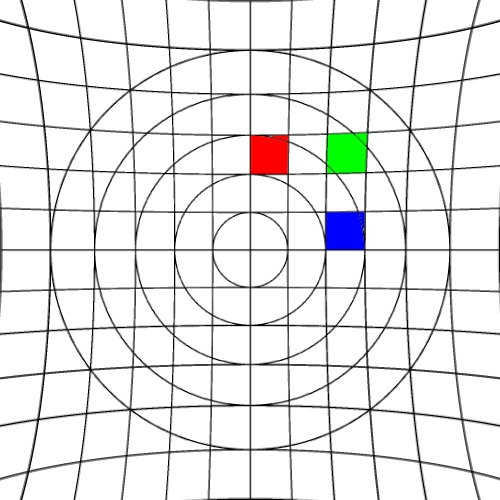
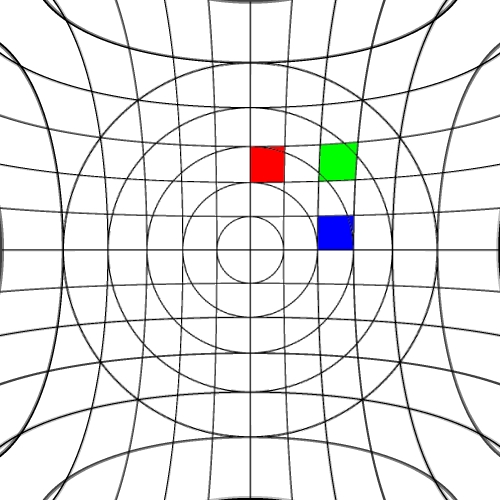
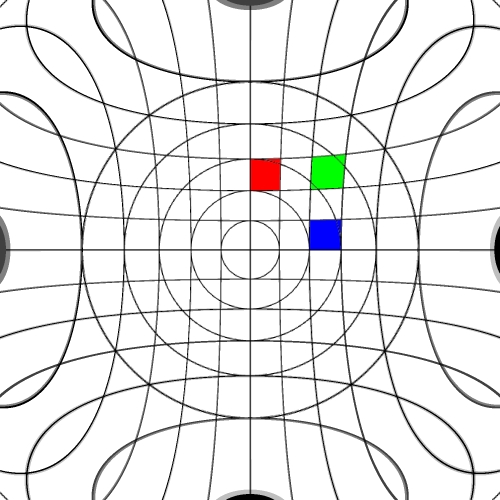
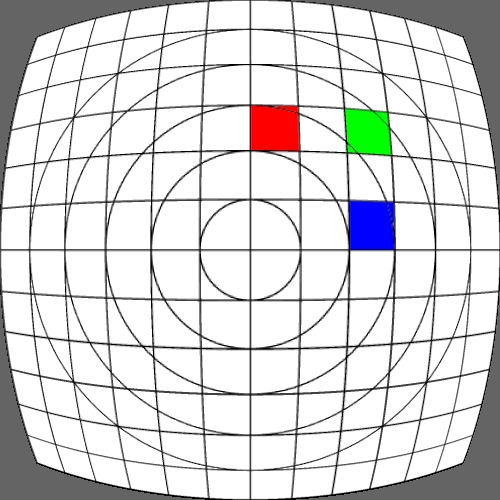
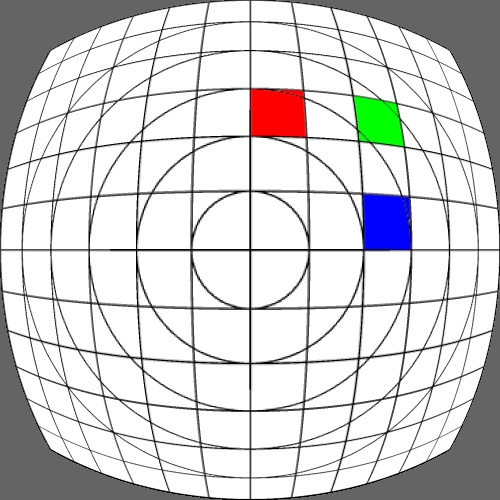
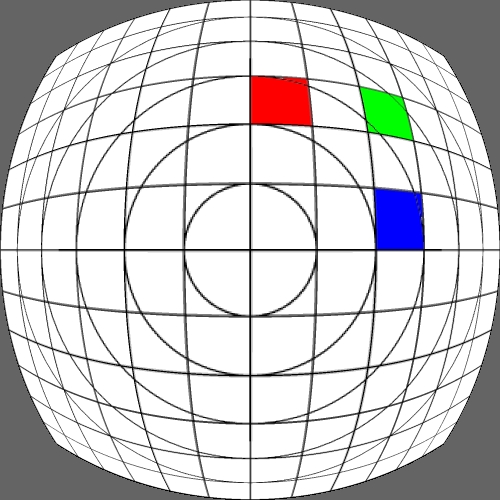
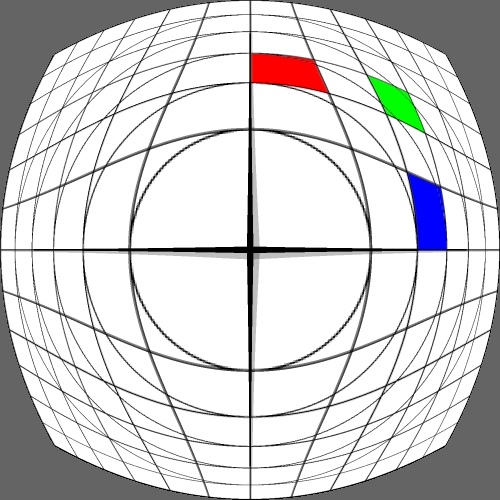
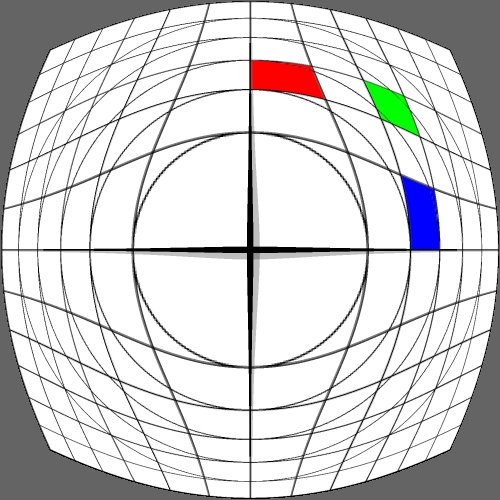
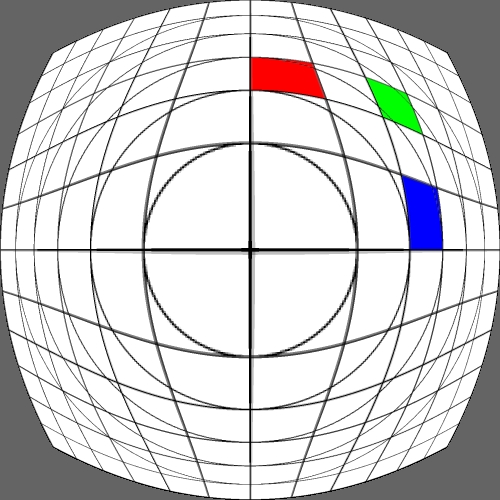
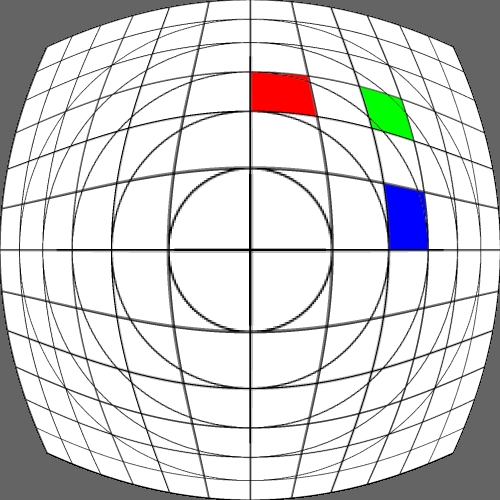
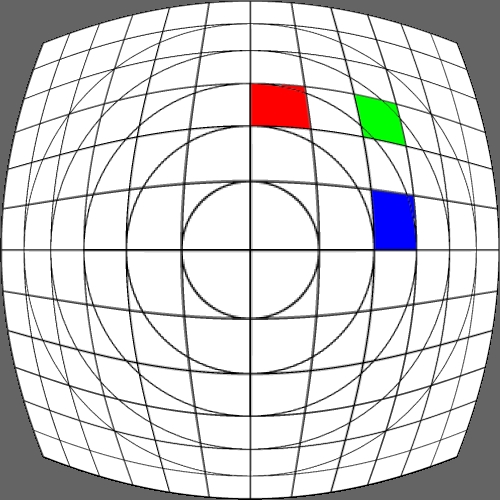
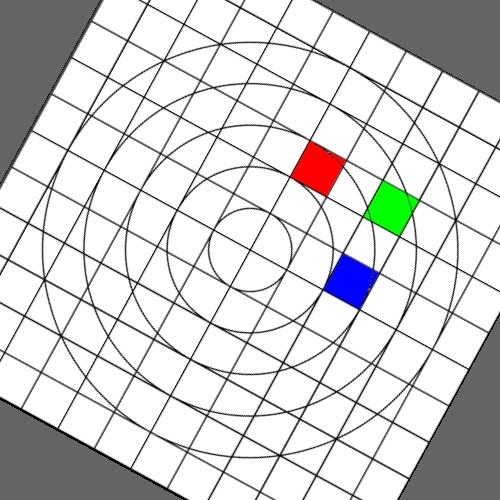
Image warping / distortion
Written by Paul Bourke
December 2002
This documents, primarily with examples, an image warping application
that was originally developed to test the simulation of various lens
types.
There are a few key ideas with image transformations such as this.
The transformation that one needs is not the function that
maps from the source image to the destination but the reverse.
What is required is to find the source pixel associated with
each pixel in the destination image. In general the image plane is
considered to be a real valued function rather than a discrete pixel
plane, this is particularly so when antialiasing is implemented.
The image coordinates are transformed from pixels (i,j) ranging from
0 to the width-1 and height-1 to normalised coordinates (x,y) ranging
from -1 to 1, this is irrespective of the image proportions
and it applies to both the source and destination image coordinates.
x = 2 i / width - 1
y = 2 j / height - 1
A key ingredient for image quality is antialiasing. In the
code given here, supersampling is used. That is, each pixel
in the destination image is sampled a number of times,
the resulting estimate from the source image are averaged
(box filter is used here)
to give a final estimate in the destination image.
Some transformation act upon the cartesian coordinates
while other are radial (polar coordinates) in nature. The r,phi coordinates
are as follows.
r = sqrt(x2 + y2)
phi = atan2(y,x)
After the radial based warp the reverse transformation back to
cartesian normalised coordinates is:
x = r cos(phi)
y = r sin(phi)
This application
(imagewarp.c)
is written as a UNIX utility that reads a
TGA file (24 or 32 bit), performs the warping as specified
by command line arguments and writes the resulting image
as a TGA file to standard output (to be redirected to a file
say).
imagewarp tgafilename [options]
Options:
-a n set antialias level (Default: 1)
-w n width of the output image (Default: 500)
-h n height of the output image (Default: width)
-m n mapping type (Default: 0)
-p1 n first parameter for mapping (Default: 0)
-p2 n second parameter for mapping (Default: 0)
-p3 n third parameter for mapping (Default: 0)
-s n scale factor (Default: 1)
-v debug/verbose mode (Default: off)
The following lists each of the image warping types supported,
other warping function can readily be added.
|