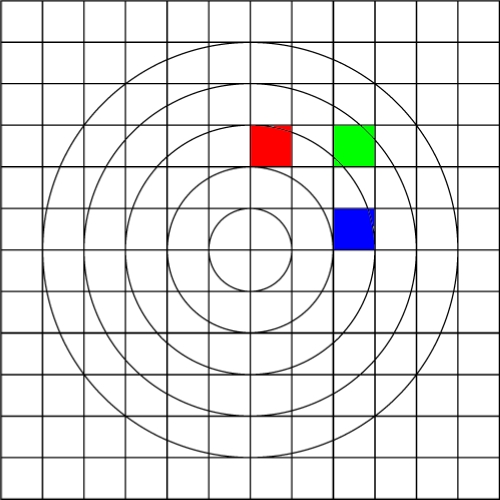
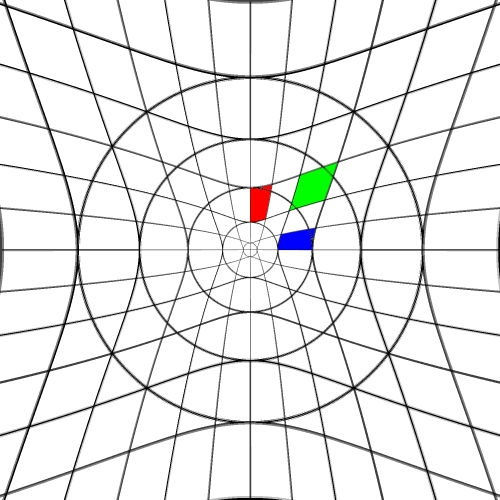
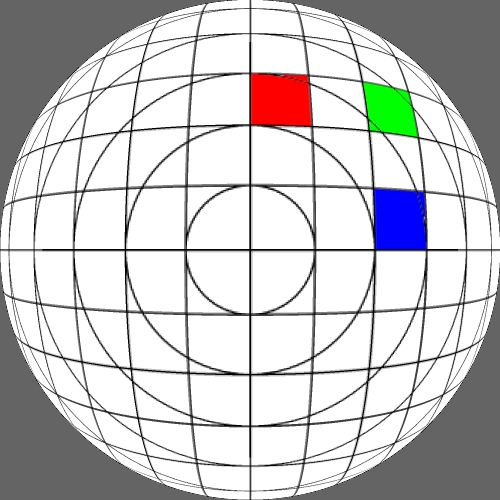
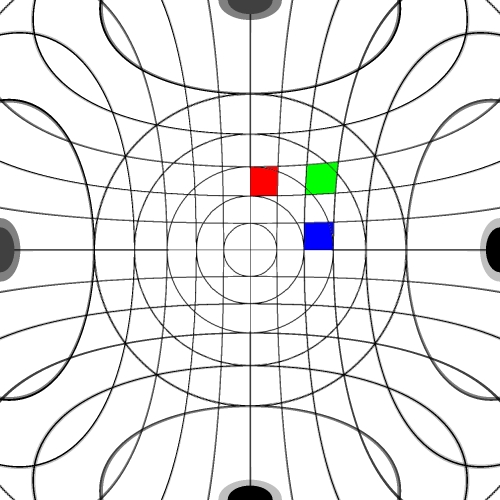
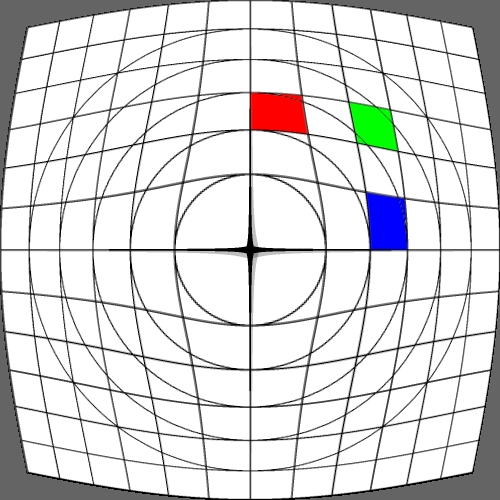
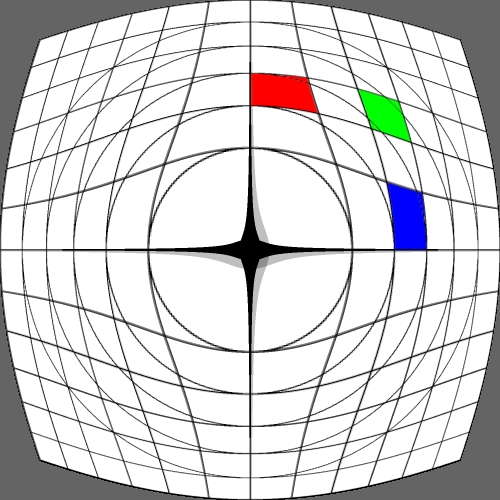
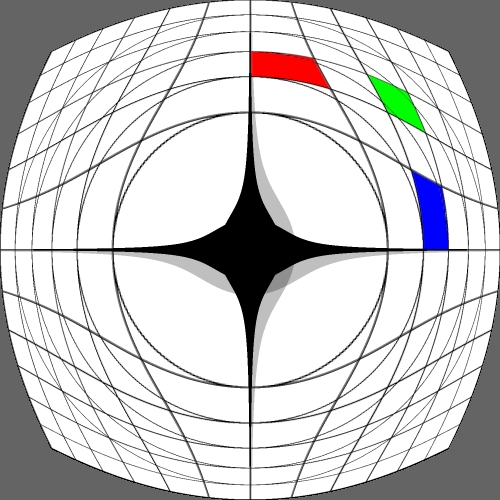
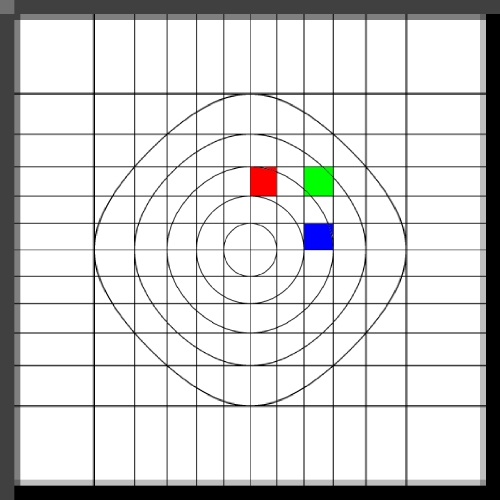
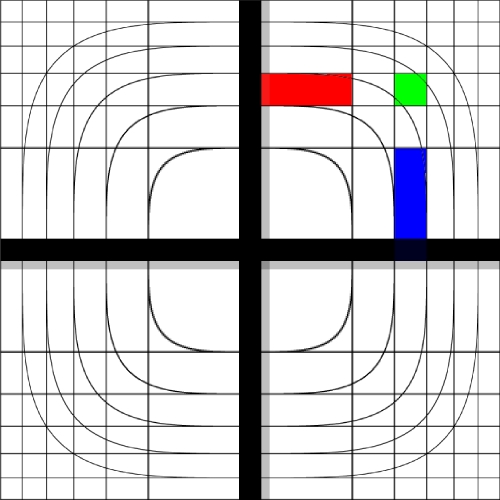
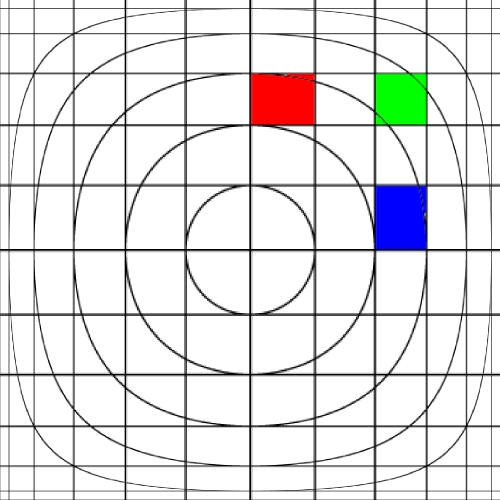
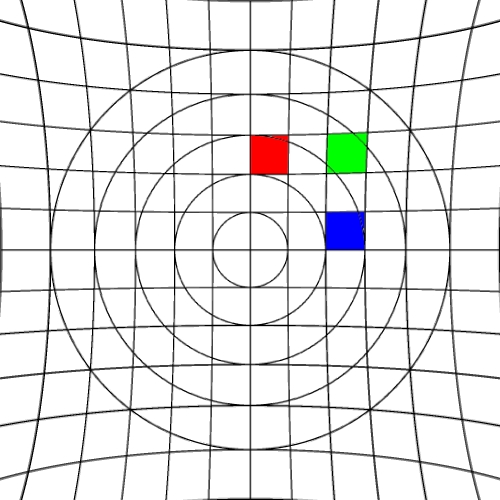
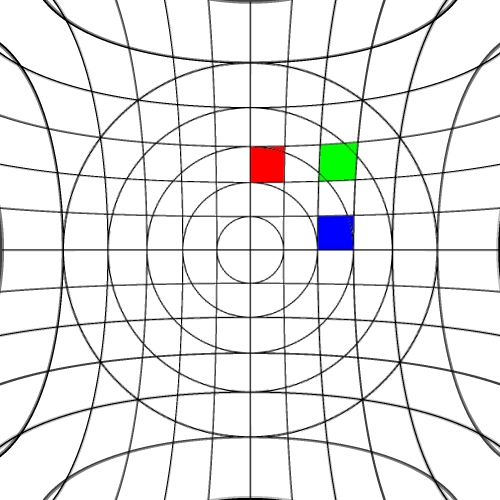
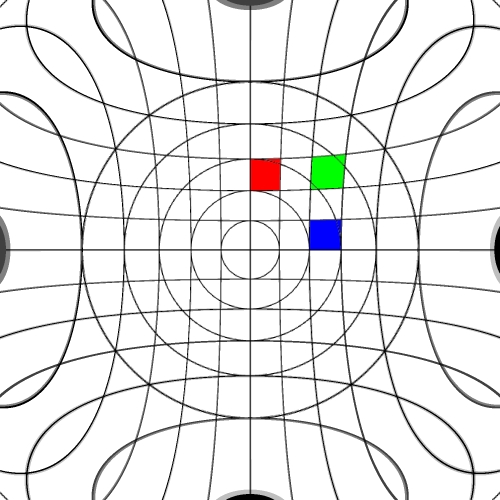
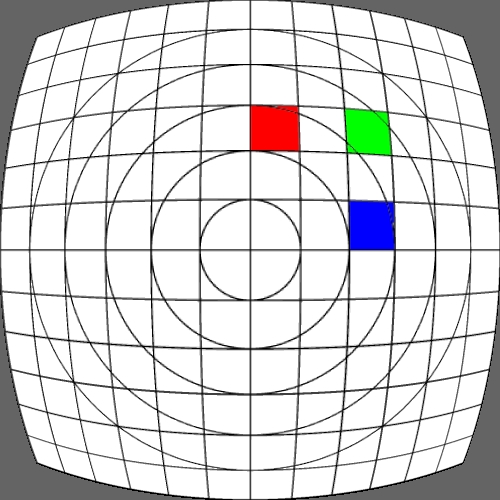
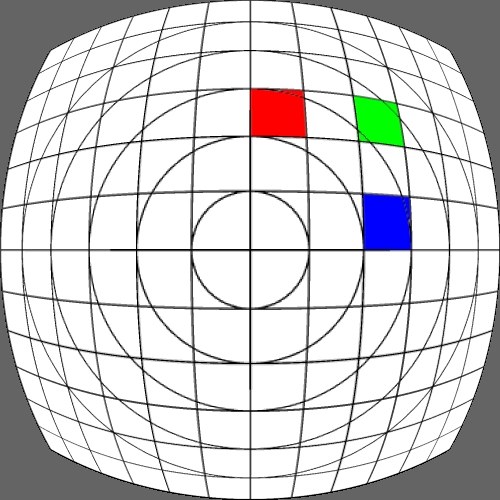
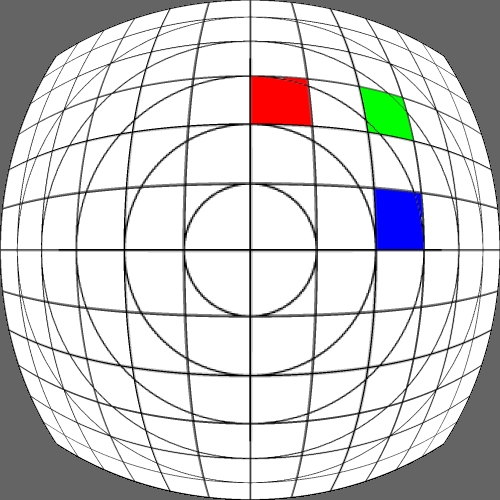
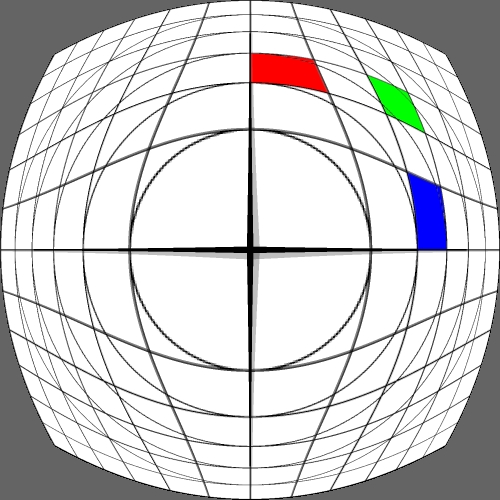
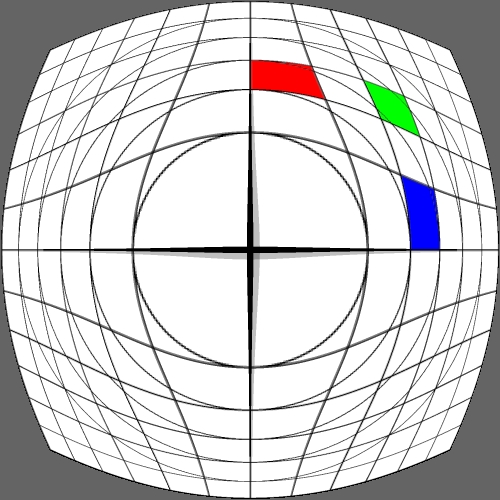
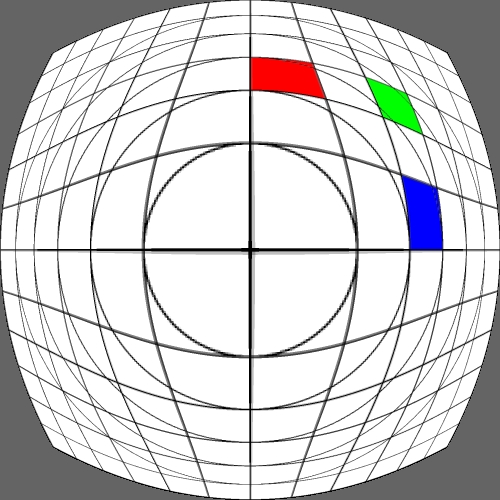
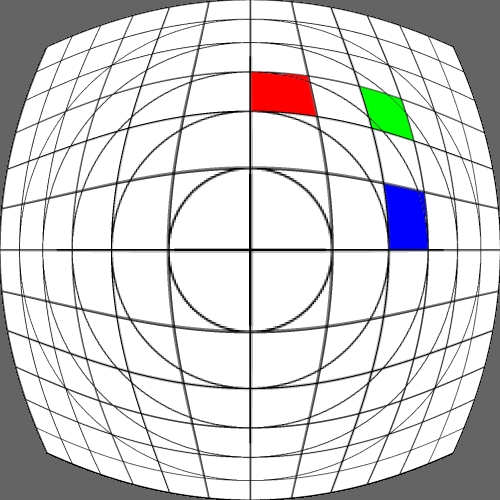
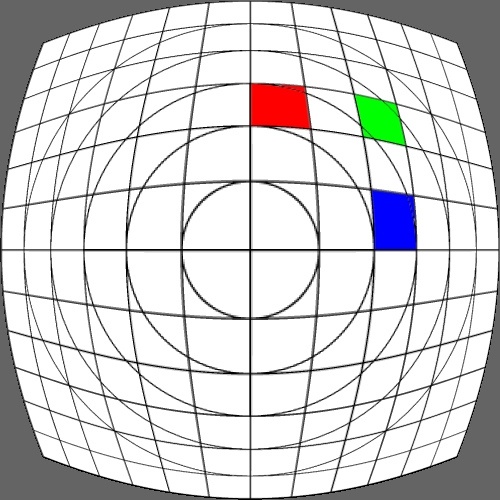
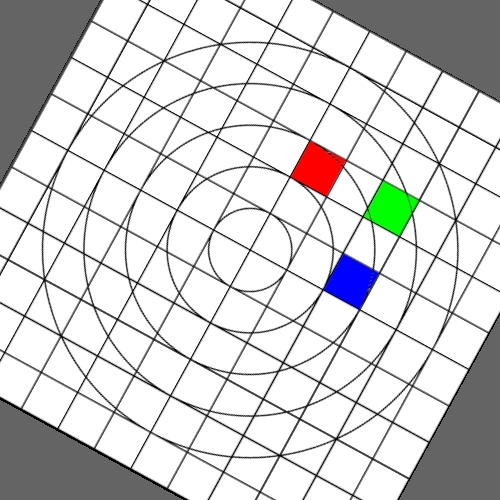
Image warping / distortion

Written by Paul Bourke
December 2002


This documents, primarily with examples, an image warping application that was originally developed to test the simulation of various lens types. There are a few key ideas with image transformations such as this.

  • The transformation that one needs is not the function that maps from the source image to the destination but the reverse. What is required is to find the source pixel associated with each pixel in the destination image. In general the image plane is considered to be a real valued function rather than a discrete pixel plane, this is particularly so when antialiasing is implemented.

  • The image coordinates are transformed from pixels (i,j) ranging from 0 to the width-1 and height-1 to normalised coordinates (x,y) ranging from -1 to 1, this is irrespective of the image proportions and it applies to both the source and destination image coordinates.

    x = 2 i / width - 1
    y = 2 j / height - 1

  • A key ingredient for image quality is antialiasing. In the code given here, supersampling is used. That is, each pixel in the destination image is sampled a number of times, the resulting estimate from the source image are averaged (box filter is used here) to give a final estimate in the destination image.

  • Some transformation act upon the cartesian coordinates while other are radial (polar coordinates) in nature. The r,phi coordinates are as follows.

    r = sqrt(x2 + y2)
    phi = atan2(y,x)

    After the radial based warp the reverse transformation back to cartesian normalised coordinates is:

    x = r cos(phi)
    y = r sin(phi)

This application (imagewarp.c) is written as a UNIX utility that reads a TGA file (24 or 32 bit), performs the warping as specified by command line arguments and writes the resulting image as a TGA file to standard output (to be redirected to a file say). 

imagewarp tgafilename [options]
Options:
-a n   set antialias level (Default: 1)
-w n   width of the output image (Default: 500)
-h n   height of the output image (Default: width)
-m n   mapping type (Default: 0)
-p1 n  first parameter for mapping (Default: 0)
-p2 n  second parameter for mapping (Default: 0)
-p3 n  third parameter for mapping (Default: 0)
-s n   scale factor (Default: 1)
-v     debug/verbose mode (Default: off)

The following lists each of the image warping types supported, other warping function can readily be added.

Source image

This is the test image: test.tga that is transformed into each of the images below.

r -> sqrt(r)
r -> 2 arcsin(r) / pi
r -> sin(pi r / 2)
r -> rp
p = 1.5
r -> rp
p = 2
r -> rp
p = 3
x -> sin(pi x / 2)
y -> sin(pi x / 2)
x -> sign(x) x2
y -> sign(y) y2
x -> 2 asin(x) / pi
y -> 2 asin(y) / pi
x -> x (1 - p r) / (1 - p)
y -> y (1 - p.r) / (1 - p)
p = 0.1
x -> x (1 - p r) / (1 - p)
y -> y (1 - p.r) / (1 - p)
p = 0.2
x -> x (1 - p r) / (1 - p)
y -> y (1 - p.r) / (1 - p)
p = 0.3
Method by H. Farid and A.C. Popescu for modest lens with good fit.
p = 0.2
Method by H. Farid and A.C. Popescu for modest lens with good fit.
p = 0.4
Method by H. Farid and A.C. Popescu for modest lens with good fit.
p = 0.6
r -> p1 10r p2 - p1
p1 = 0.049
p2 = 1.280
r -> p1 r3 + p2 r2 + p3 r
p1 = 0.819
p2 = 0.046
p3 = 0.152
Janez Pers, Stanislav Kovacic An Alternative Model for Radial Distortion in Wide-Angle Lenses (Single parameter model)
p = 0.1
Janez Pers, Stanislav Kovacic An Alternative Model for Radial Distortion in Wide-Angle Lenses (Single parameter model)
p = 0.2
Janez Pers, Stanislav Kovacic An Alternative Model for Radial Distortion in Wide-Angle Lenses (Single parameter model)
p = 0.3
Rotation
phi = phi + p
p = 0.5