Image Filtering in the Frequency DomainWritten by Paul BourkeJune 1998
See also: 2D Fourier Transform, and
Fast Fourier Transform
The following will discuss two dimensional image filtering in the
frequency domain. The reason for doing the filtering in the frequency
domain is generally because it is computationally faster to perform
two 2D Fourier transforms and a filter multiply than to perform a
convolution in the image (spatial) domain. This is particularly so
as the filter size increases. Example 1 - GeneralThe following example will apply "ideal" low, high, and band pass filters to a 2 dimensional rectangular pulse with low level added noise. For each step in the process two representations will be given, the image and a surface rendering. Seeing both together can often give different clues as to what is going on. The original signal is a rectangular pulse with added noise.
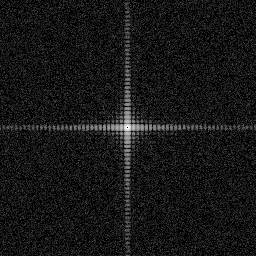
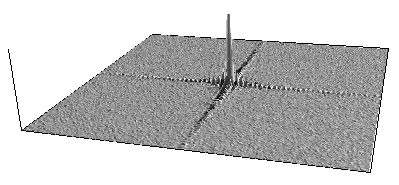
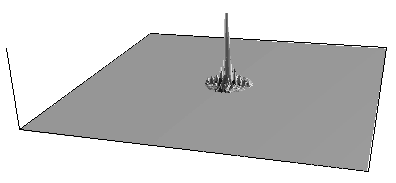
The Fourier transform of the rectangular pulse is the two dimensional
equivalent of the sync function, the Fourier transform of white noise
is a constant.
Applying a low pass filter in the frequency domain means zeroing all frequency components above a cut-off frequency. This is similar to what one would do in a 1 dimensional case except now the ideal filter is a cylindrical "can" instead of a rectangular pulse.
The result transformed back into the spatial domain. As expected the
high frequency components have been removed. The rectangular pulse
is "rounded" since high frequency components were required for the
transition.
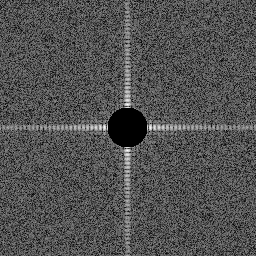
Applying a high pass filter frequency domain is the opposite to
the low pass filter, that is, all the frequencies below some cut-off
radius are removed. Note the apparently higher noise levels are
false, the graphs are auto scaling and thus the field only appears
larger because of the removal of the low frequency components.
Transformed back into the spatial domain shows that the noise field
is retained as well as the transitions (edges) of the rectangular pulse.
Applying a band pass filter, frequency domain.
Transformed back into the spatial domain
Sketch showing how the 4 quadrants returned from the 2D Fourier transform are rearranged so as to position the DC component in the middle of the image. A very clear understanding of the position of DC, the Nyquist frequency, and positive/negative frequencies is necessary to get this translation correct. 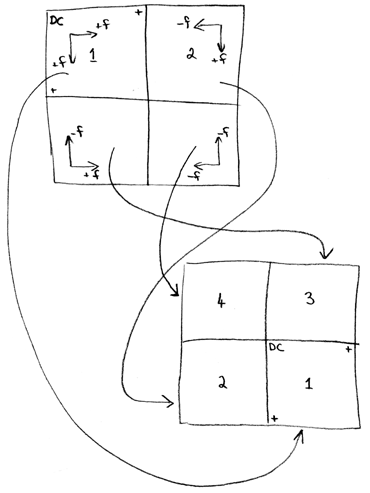
Example 2 - Smooth low pass filters
As with time series filtering, using ideal rectangular filters can
result in unwanted ringing. In two dimensions instead of using a
radial rectangular filter (a can) one can smooth the transition
between the stop and pass band. This is often done using Hanning
or Hamming windows which are rectangular windows smoothed by
cosine functions.

The "can" type low pass filter is shown below on the left along with the filtered step function on the right.
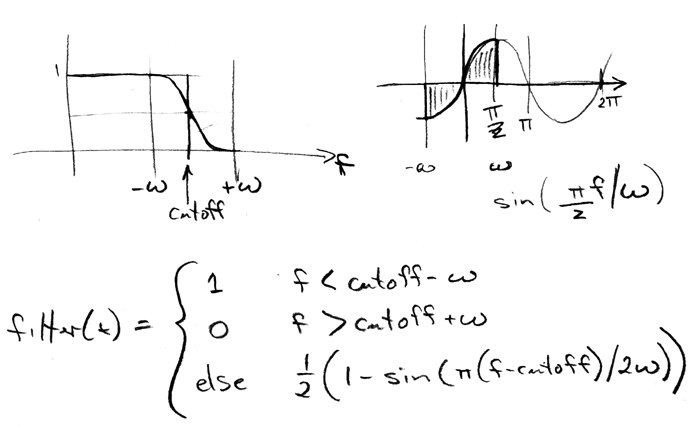
In this next image a smoothed version of the filter is used (left) and the filtered result is again shown no the right. The ringing in the region distant to the step is significantly reduced.
Example 3 - Smooth high pass filterIn a less artificial example of using smooth filters, consider a high pass filtering of the following photograph. 
The following uses the sharp high pass filter from example 1 shown on the left and the resulting filtered image is on the right.
The following uses a smooth version of the same high pass filter (left) and the filtered image is shown on the right. The ringing is greatly reduced, see the large regions of constant (low frequency) content such as the path or the door.
|