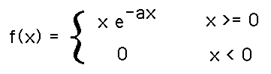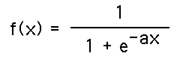Miscellaneous functionsWritten by Paul BourkeJanuary 2001
Zeta function
The Zeta function (sometimes called the Riemann Zeta Function) was defined by Euler as 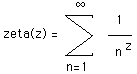
Where z is a complex number with the real part greater than 1. An alternating sign version is defined as 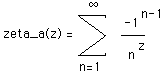
Where the real part of z must be greater than 0. This allows the zeta function to be defined for real values of z greater than 0 but not 1 as follows. 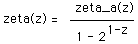
There are some special values of the zeta function that are known, for example zeta(2) = pi2 / 6, zeta(4) = pi4 / 90, zeta(6) = pi6 / 945. For the alternating zeta function zeta_a(2) = pi2 / 12, zeta_a(4) = 7 pi4 / 720. A well known (and unproven) hypothesis is called the Reimann Hypothesis is that all values of z for which zeta(z) = 0 are of the form 1/2 * i y. That is, a complex number with real part of 1/2.
Alpha Function
SINC functionThe so called "sinc" function turns up in many application areas, perhaps most often in signal processing and Fourier analysis as it is the form of the Fourier transform of a rectangular pulse. The usual definition is 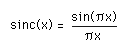 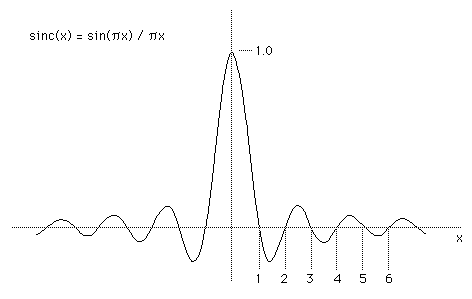 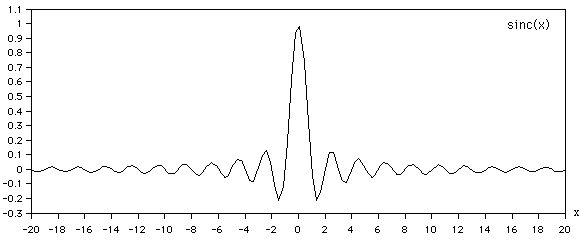 Generating the function in software is straightforward noting the special case near the origin. Since sin(x) is very close to linear as x -> 0, there are no numerical problems using a low order polynomial expansion for sin(x) in this region.
Factorial and the Gamma FunctionThe factorial of an integer n is normally written as n! and defined as
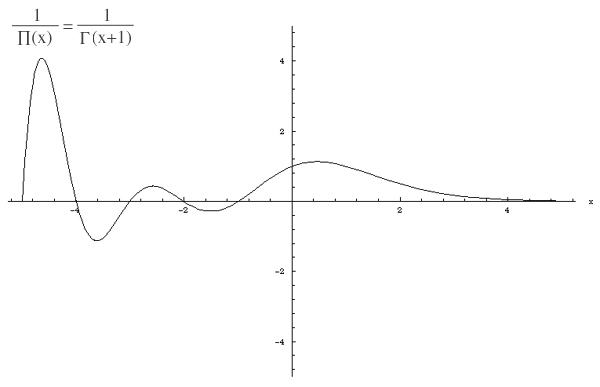
The factorial is a special case of the more general Gamma function which can be applied to any real (or complex) number. The Gamma function is defined as 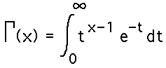
When the Gamma function is applied to the positive integers its relationship to factorials is as follows Note:
Gamma(x+1) = 1 - 0.577191652 x + 0.988205891 x2 - 0.897056937 x3 + 0.918206857 x4 - 0.756704078 x5 + 0.482199394 x6 - 0.193527818 x7 + 0.035868343 x8 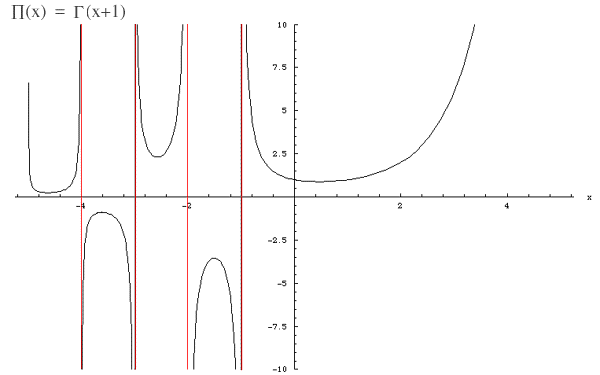
/*
Natural log of the gamma function (xx > 0)
Derived from "Numerical Receipes in C"
*/
double LnGamma(double xx)
{
int j;
double x,y,tmp,ser;
double cof[6] = {
76.18009172947146, -86.50532032941677,
24.01409824083091, -1.231739572450155,
0.1208650973866179e-2,-0.5395239384953e-5
};
y = x = xx;
tmp = x + 5.5 - (x + 0.5) * log(x + 5.5);
ser = 1.000000000190015;
for (j=0;j<=5;j++)
ser += (cof[j] / ++y);
return(log(2.5066282746310005 * ser / x) - tmp);
}
References
Handbook of Mathematical Functions
Gabor Function
The Gabor function is the name given to a Gaussian weighted sinusoid. In higher dimensions the sinusoid only varies in one dimension while the Gaussian envelop applies in all dimensions. The function is named after Dennis Gabor who used this function in the 1940s and later J Daugman who proposed the function to describe the spatial response of cells in visual stimuli experiments. 1 Dimension The equation in 1D is as follows
The center of the function is at "m", the width is given by the standard deviation "s" of the Gaussian, the number of cycles within the envelop is T.
The function for various values of the cosine period "T". 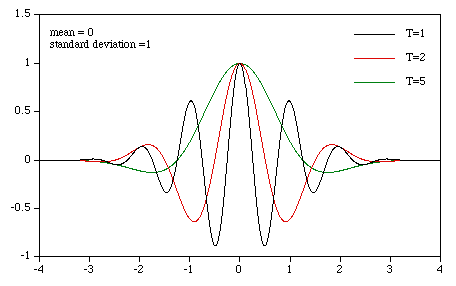
2 Dimensions
The equation in 2D is as follows
The parameters have a similar meaning in 2 dimensions except that now there are two parameters for the center (mx, my) and standard deviation (sx, sy). Top intensity shaded view
3D perspective surface 
Note
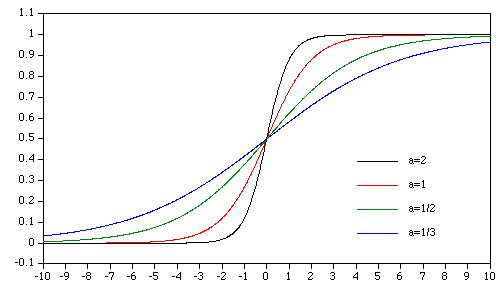
Sigmoid Function
This function arises in many dynamical systems because it is the solution to a first order differential equation
This equation describes simple exponential growth dynamics with a linear limiting control, such systems are often called logistic growth or Verhulst growth. The solution is
Gompertz Function
The Gompertz equation arises from models of self-limited growth where the rate decreases exponentially with time, for example, as the solution to the first order differential equation The solution is of the form
where a and k are greater than 0. 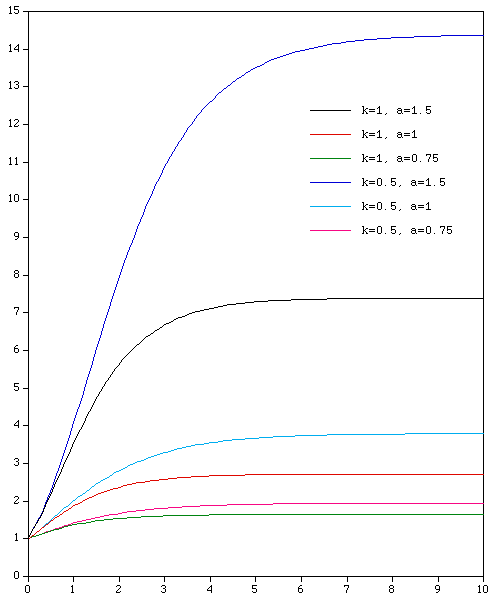
Biexponential FunctionThe biexponential function is defined as follows. 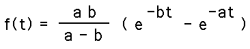 Where a,b,t greater than or equal to 0, a is not equal to b. When a = b the function is f(t) = a2 t e- a t The form of the function for one value of a and a number of different values of b is shown below. 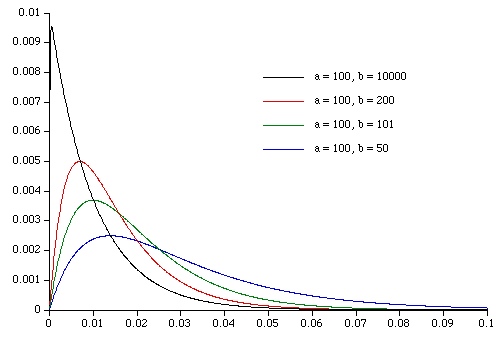 Notes
There is a computationally nice result when using a biexponential in a convolution, say ft = biexpt * gt Normally one would need to remember the last N terms of gt where N is determined by how far along the biexponential one wished to perform the convolution. It can be shown however that the convolution can be performed with a minimum of storage as Where
and
Miscellaneous Series and Sequences"He must be a 'practical' man who can see no poetry in mathematics." W.F. White
Definitions
Arithmetic series a + (a+d) + (a+2d) + (a+3d) + ..... + (a+(n-1)d) = n (2 a + (n - 1) d) / 2Geometric series a + ar + ar2 + ar3 + ..... + arn-1 = a (1 - rn) / (1 - r), for r not equal to 1Exponential series 1 + x + x2/2! + x3/3! + ..... = exLogarithmic series x + x2/2 + x3/3 - x4/4 + ..... = loge(1 + x)Binomial series (1 + x)n = 1 + nx + n(n-1)x2/2! + n(n-1)(n-2)x3/3! + .....Converges for all x if n is positive. For negative n it converges if |x| is less than 1
Sine and Cosine x - x3/3! + x5/5! - x7/7! + ... = sin(x) 1 - x2/2! + x4/4! - x6/6! + ... = cos(x)Harmonic Series 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + . . . . + 1/n + . . . = infinityThe sum for large n is approximately ln(n) + 0.5772156649... (Eulers constant)
Prime Harmonic Series 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/23 + . . . .Miscellaneous Algebraic Series 1 + 2 + 3 + 4 + .... + n = n (n + 1) / 2 12 + 22 + 32 + 42 + ..... + n2 = n (n + 1) (2 n + 1) / 6 13 + 23 + 33 + 43 + ..... + n3 = n2 (n + 1)2 / 4Fibonacci sequence F[n] = F[n-1] + F[n-2] for integers F[0] and F[1] 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . . .Q sequence Q[n] = Q[n-Q[n-1]] + Q[n-Q[n-2]] Q[0] = 1, Q[1] = 1 1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 6, 8, 8, 8, 10, 9, 10, 11, 11, 12, . . .
Pascals triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
: : : : : : :
Each number is the sum of the two numbers above it to the left and right.
The triangle grows downwards.
Perfect number sequence 6, 28, 496, 8128, 33550336, 8589869056, 137438691328, 2305843008139952128, ... These number all satisfy 2p-1 (2p-1) where 2p-1 is prime, called a Mersenne prime. Note: p will also be prime.
Trigonometric Identities
sin(a +/- b) = sin(a) cos(b) +/- cos(a) sin(b)
cos(a +/- b) = cos(a) cos(b) -/+ sin(a) sin(b)
2 sin(a) cos(b) = sin(a + b) + sin(a - b)
2 cos(a) cos(b) = cos(a + b) + cos(a - b)
2 sin(a) sin(b) = cos(a - b) - cos(a + b)
tan(a) +/- tan(b)
tan(a +/- b) = -------------------
1 -/+ tan(a) tan(b)
sin(2 a) = 2 sin(a) cos(a)
cos(2 a) = 1 - 2 sin(a) sin(a) = cos(a) cos(a) - sin(a) sin(a) = 2 cos(a) cos(a) - 1
2 tan(a)
tan(2 a) = -----------------
1 - tan(a) tan(a)
a + b a - b
sin(a) + sin(b) = 2 sin(-----) cos(-----)
2 2
a + b a - b
sin(a) - sin(b) = 2 cos(-----) sin(-----)
2 2
a + b a - b
cos(a) + cos(b) = 2 cos(-----) cos(-----)
2 2
a + b a - b
sin(a) - sin(b) = 2 sin(-----) sin(-----)
2 2
sin(a) sin(a) + cos(a) cos(a) = 1
tan(a) tan(a) = sec(a) sec(a) - 1
Substituting t = tan(a/2) then
2 t 1 - t t 2 t
sin(a) = ------- cos(a) = ------- tan(a) = -------
1 + t t 1 + t t 1 - t t
Definitions
sec(a) = 1 / cos(a) cosec(a) = 1 / sin(a)
tan(a) = sin(a) / cos(a) cot(a) = 1 / tan(a)
eia = cos(a) + i sin(a) where i = sqrt(-1)
The Normal or Gaussian distribution plays a central role in statistics and has been found to be a very good model for many continuous distributions that occur in real situations. The Gaussian function with mean (m) and standard deviation (s) is defined as follows: 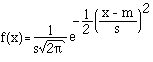
The function is symmetric about the mean, it gains its maximum value at the mean, the minimum value is at plus and minus infinity. The distribution is often referred to as "bell shaped", it has the following typical form. 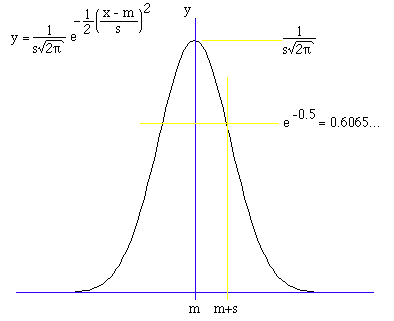
At one standard deviation from the mean the function has dropped to about 2 thirds of its maximum value, at two standard deviations it has fallen to about a seventh of its maximum value. The area under the function one standard deviation from the mean is about 0.682. Two standard deviations it is 0.9545, and three standard deviations it is 0.9973. The total area under the curve is 1, as the standard deviation is increased the curve broadens, for example the following shows the distribution for a number of values of s. 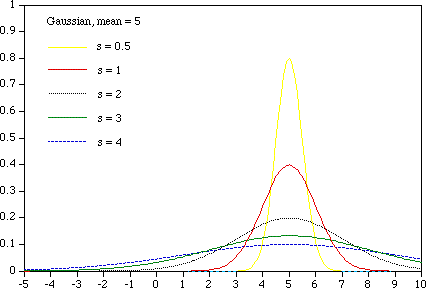
2D Gaussian
For a radially symmetric 2D Gaussian centered at the origin (mean = 0) 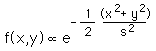
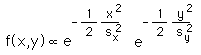  The total volume under a 2D Gaussian is 2 pi sx sy.
The probability distribution function for a Poisson process is defined as Lambda is often a rate per unit time, distance, or area.
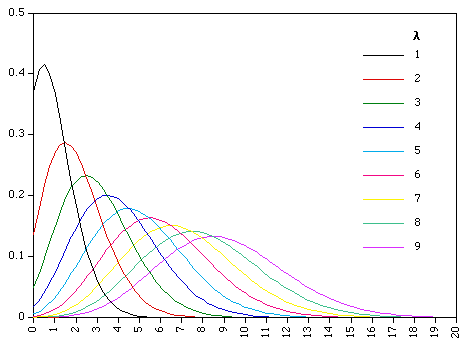
It satisfies the main requirement for a probability density function, namely that 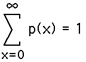
For the proof of this consider the Maclaurin infinite series expansion 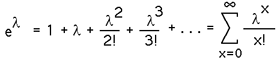
A binomial process with large n (number of samples or events) and small p (probability of an event) but such that the mean np is constant tends to Poisson. lambda = np. The variance of a Poisson process is equal to the mean.Details - Factorial of a continuous variable y! for a continuous variable is defined using the gamma function, namely Gamma(y+1). A snippet of C code based on the algorithm in "Numerical Recipes in C" is given below for computing the natural logarithm of Gamma(y) for y > 0.
double LnGamma(double xx)
{
int j;
double x,y,tmp,ser;
double cof[6] = {
76.18009172947146, -86.50532032941677,
24.01409824083091, -1.231739572450155,
0.1208650973866179e-2,-0.5395239384953e-5
};
y = x = xx;
tmp = x + 5.5 - (x + 0.5) * log(x + 5.5);
ser = 1.000000000190015;
for (j=0;j<=5;j++)
ser += (cof[j] / ++y);
return(log(2.5066282746310005 * ser / x) - tmp);
}
The probability density function for a gamma distribution is given in most general terms as 
where a and b are both greater than 0. The "standard" gamma function is often quoted as having B = 1. The gamma distribution formula above requires the evaluation of the gamma function defined as 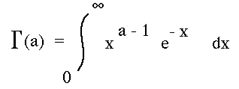
Examples of the gamma distribution for a range of values of a but a fixed value of B=1 are shown below. If a <= 1 then the distribution is always decreasing. 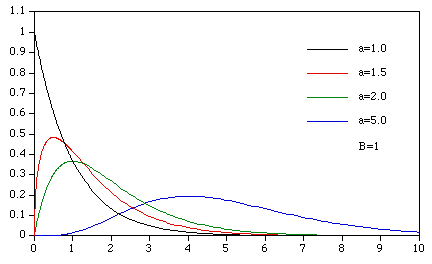
The following shows the gamma distribution with a fixed value of a=2 and various values of B. B acts mostly to stretch the distribution in the x direction.
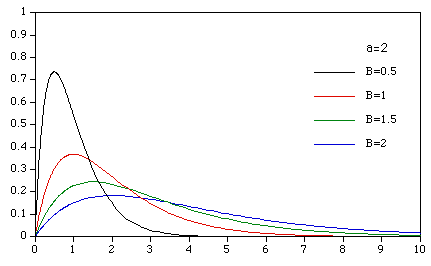
The mean of a gamma distribution is the product of a and B. The variance is the product of a and the square of B. variance = a B2
The exponential distribution is a special case of the gamma distribution where a=1 and B = 1/lambda.
The probability distribution function of an exponential distribution is given by 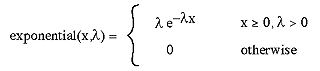
The mean is 1/lambda, the variance is 1/lambda2 Integrating the above gives the cumulative distribution 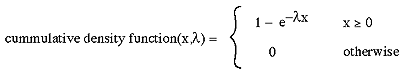
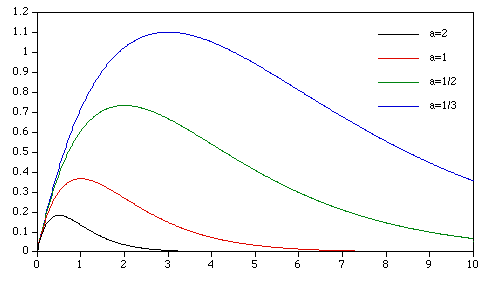
Some examples of the exponential distribution for various values of lambda are shown below: 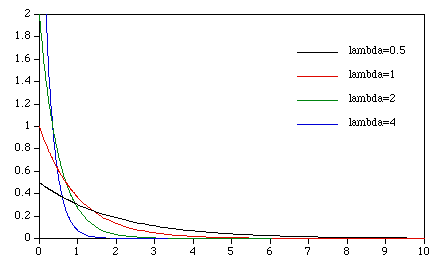 To generate an exponential distribution with a mean "m" from a uniform distribution "u" on (0,1) use -m ln(u).
The probability distribution of a narrow band noise process n(t) was formulated by Rice in papers published in the Bell Laboratories Journal, 1944 and 1945. It can be derived by considering a complex phaser
where r(t) is the magnitude or envelope and phi(t) is the phase. This can also be written in terms of its real and imaginary parts (in-phase and quadrature components) as 
If both random processes x(t) and y(t) are Gaussian distributed with the same variance and zero mean then the probability density functions P(x) and P(y) are given by 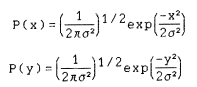
Assuming x and y are statistically independent then 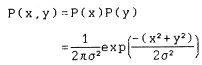 Transforming differential areas using
gives the joint probability density function as
Since this is independent of phase the random variables r and phi are statistically independent and therefore Then
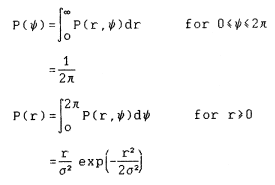
This is normally called the Rayleigh Distribution. See figure A.1 for plots of this distribution for various values of the variance. 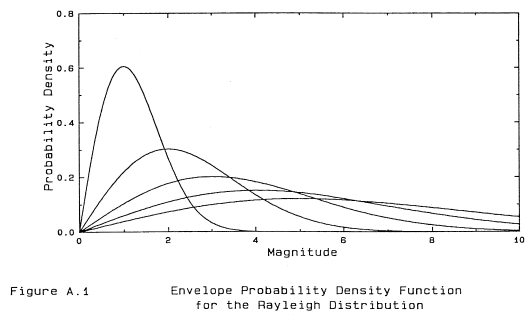
The probability distribution of a sinusoid plus narrow band noise is called the Rice Distribution. The expression for a cosinusoid of amplitude A and noise process, as for the Rayleigh distribution, can be written as
The Rician probability density function is derived as for the Rayleigh distribution by considering the in-phase and quadrature components. The joint probability density function in this case is
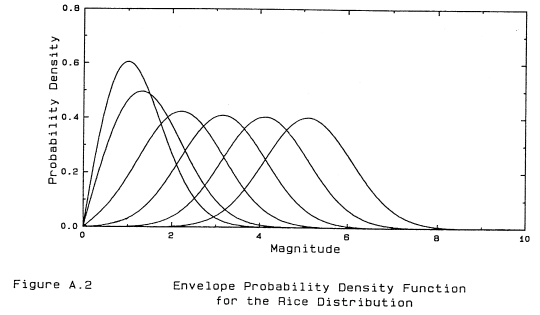
where now r and phi are no longer statistically independent variables. The envelope distribution P(r) is 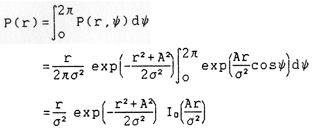
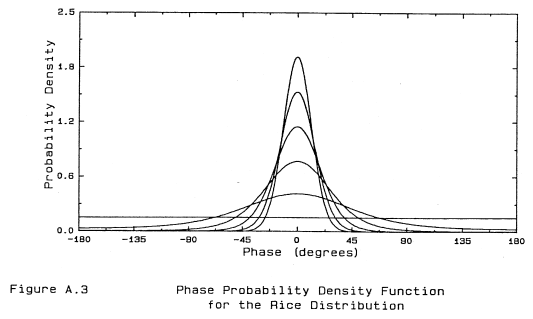
where Io is the zero order modified Bessel function of the first kind (Abramowitz 1970) given by The phase distribution is
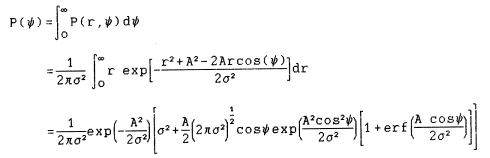 where erf(x) is the error function (Abramowitz 1970) defined as
Figure A.2 and A.3 show the Rice (magnitude and phase) distributions for various values of the signal-to-noise power ratio.
|