Frustum Culling
Written by Paul Bourke
November 2000
Before geometry is sent to a rendering engine it is often desirable
to determine whether or not it is visible and therefore need not
be rendered. While rendering engines such as OpenGL clip the geometry
themselves, it still requires the overhead of the geometry being sent to
the engine.
In most 3D rendering applications a perspective projection is applied.
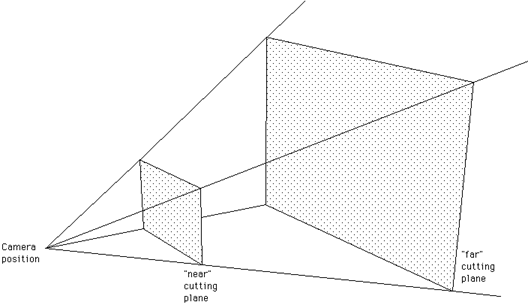
The volume of space that is visible is called the view frustum, an example
is shown below. It is defined by four planes (top, bottom, left, right)
and optionally a front and back cutting plane.
The near and far cutting planes are normally specified as scalars, distances
along the view direction vector. The sides and top/bottom can be specified
directly or they are computed from the camera aperture. In some packages
this is calculated from the
vertical aperture, some on the horizontal,
whichever is chosen the other is fixed given the ratio of the window
width and height.
In order to determine whether part of a primitive is inside the frustum it
is necessary to check that every vertex in the primitive is outside
the volume. To determine this, compute the vertices of each plane
making up the frustum. Each plane can be written in the form,
Ax + By + Cz + D = 0. The constants A,B,C,D can be calculated from any
three points on the planes (since all four points are coplanar) say
(x1,y1,z1),
(x2,y2,z2), and
(x3,y3,z3) as follows:
A = y1 (z2 -
z3) + y2
(z3 - z1) + y3
(z1> - z2)
B = z1 (x2 - x3) +
z2 (x3 - x1) +
z3 (x1 - x2)
C = x1 (y2 - y3) +
x2 (y3 - y1) +
x3 (y1 - y2)
- D = x1
(y2 z3 - y3 z2) +
x2 (y3 z1 - y1 z3) +
x3 (y1 z2 - y2 z1)
In order to test whether a point (x,y,z) is on the left or right of
the plane compute Ax + By + Cz + D. If the result is greater than zero
then the point is on the same side as the normal (A,B,C), if less than
zero then it's on the opposite side, if zero then it lies on the plane.
Notes
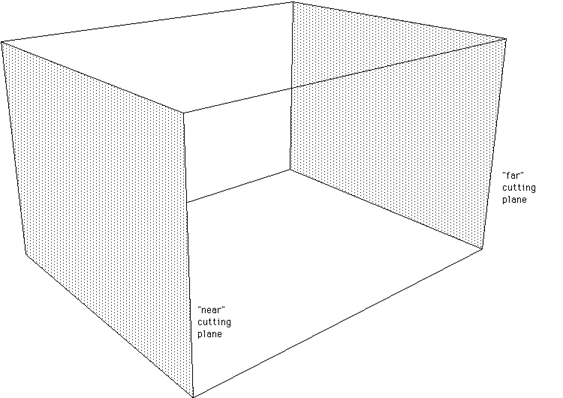
A parallel (orthographic) projection still consists of a viewing
volume but it is a much simpler shape, a box. Clipping against such a
volume uses the same techniques discussed here.
In many applications there would be significant overhead in testing every
single point of low level primitives. The alternative is to group primitives
together into higher level shapes, then one simply tests the
vertices of the bounding box of the
shape to determine whether it is inside or outside the frustum.
When the shape intersects the view frustum one can choose whether
to further test the individual primitives or simple pass the
whole shape to the rendering engine.
|

