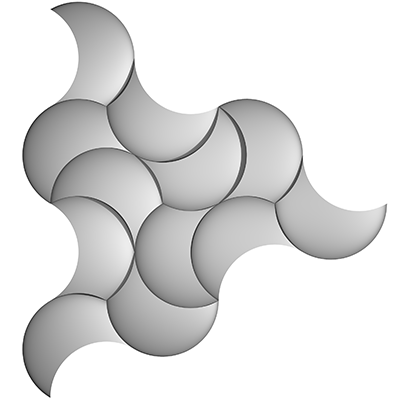
Tiling with TricurvesWritten by Paul BourkeInspired by Tim Lexen February 2017
There are a number of ways one can define a tricurve, the one used here is to start with an arc of some angle, replicate two identical curves ard rotate each about some angle about the ends of the arc. The Tricurve is the enclosed area.
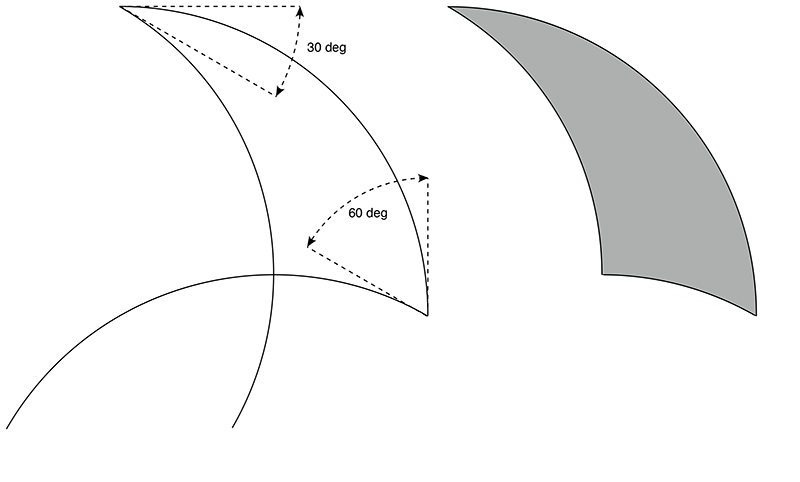
For the purposes of tiling only certain angles are suitable, typically those that are integer divisors of 360 degrees. Tricurves will be named according to their three interior angles listed in increasing order, so the above is called 30-60-90.
The apparent 3 dimensionality and shading of some of the figures here is achieved by using CSG, Solid Constructive Geometry. For example, a sphere may be used to represent the initial arc and subtracted from that two suitably positioned and rotated cylinders. On the following, view from the top, the red and blue cylinders are subtracted from the grey sphere. 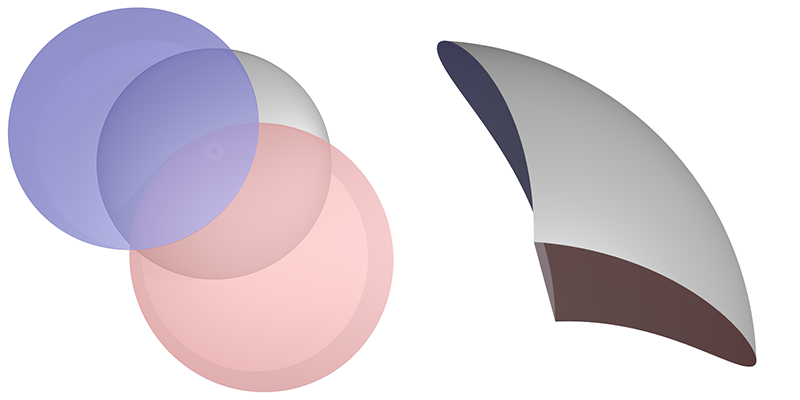
The above starts with a 90 degree arc, the following starts with a 180 degree arc. 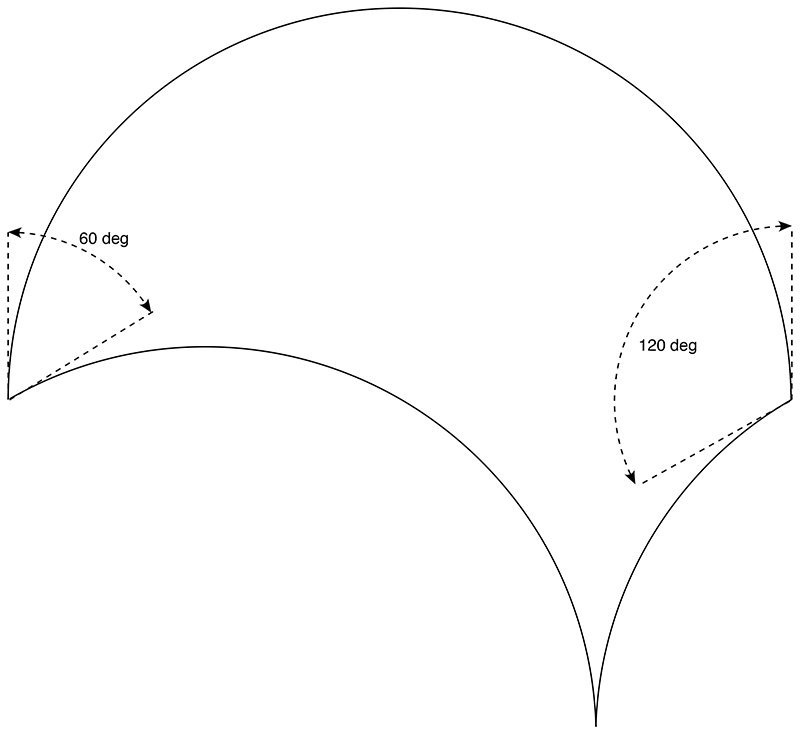



Contributions by Tim Lexen
Introduction: tricurves.pdf 
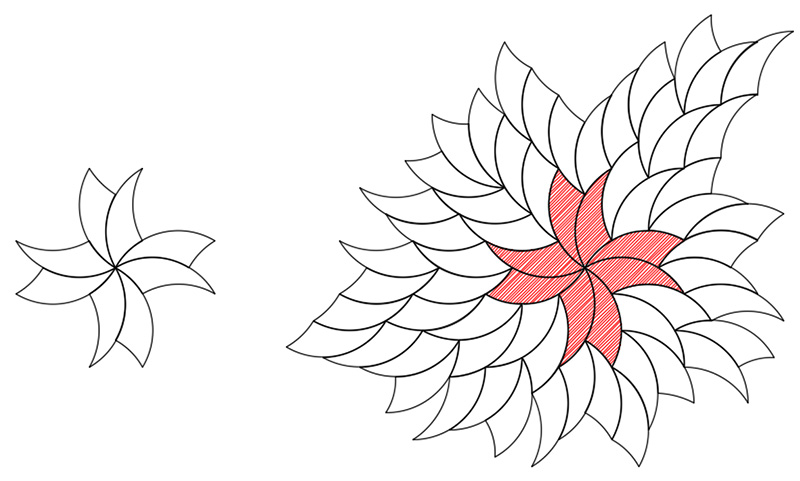
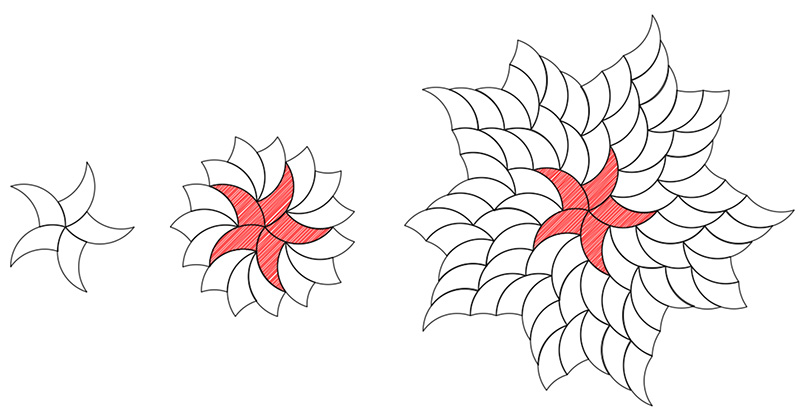
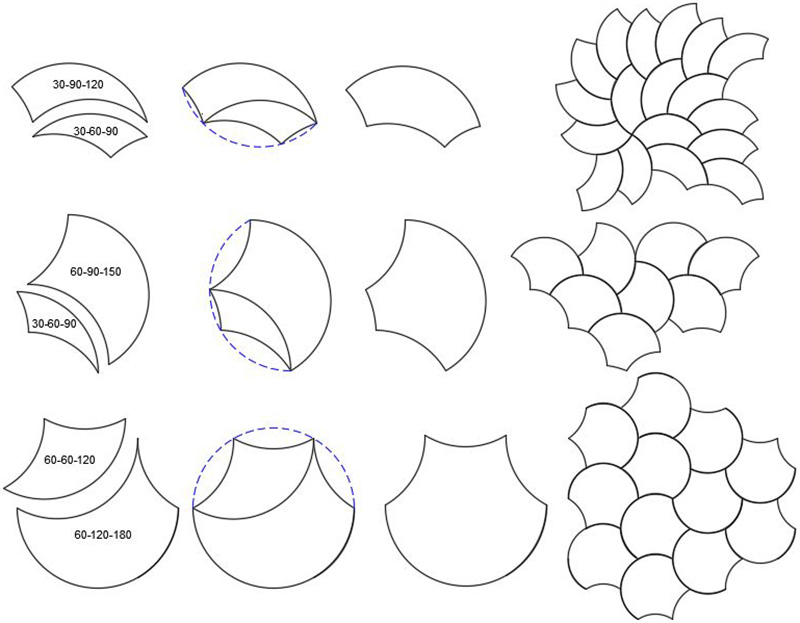
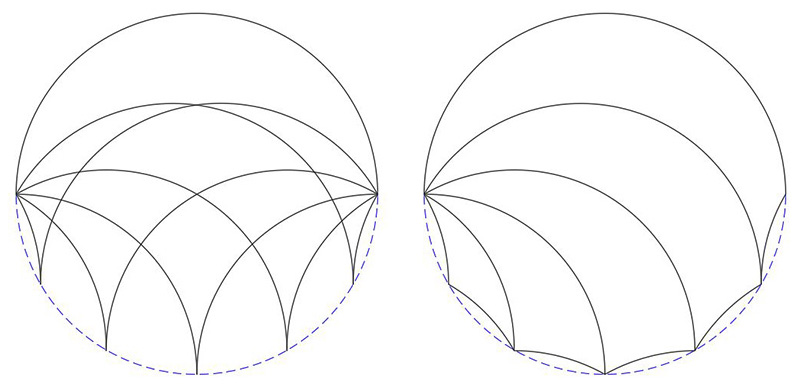
|