Modelling a Tear Drop

Written by Paul Bourke
February 1995

Sample C code

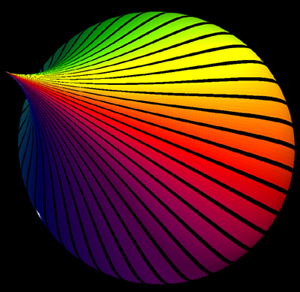
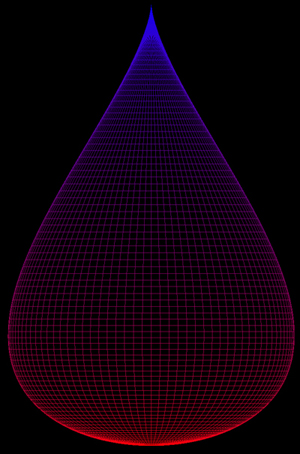
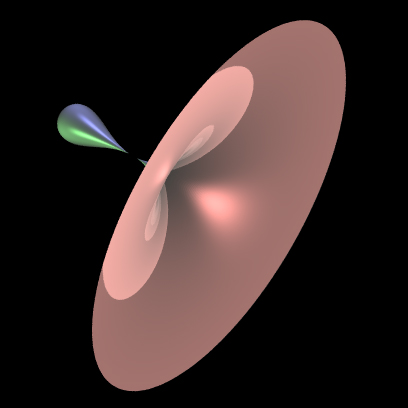
The is following describes the parametric equations which give rise to an approximate model of a drop of water, for example, a tear drop. Rendered examples are shown on the right.

The equations as functions of longitude phi and latitude theta are:

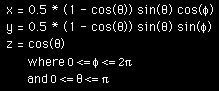
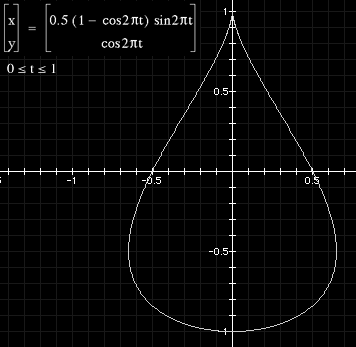
When theta is 0 there is a discontinuity at the apex where (x,y,z) = (0,0,1)
  



 

Glass model

©2002 Rolfe A. Leary

Glass works by Glas-Smedjen
Andrew J. Brown & Nanna Backhaus Brown

  

 
World Trade Center Memorial

The inspiration for an entry to the World Trade Center Memorial Competition by Peter Taylor Ernest (Architect) and Rolfe Leary.