Parallelohedron
Written by Paul Bourke |
|
Cube
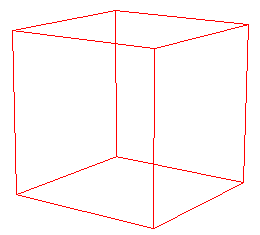
|
4 -1 -1 -1 1 -1 -1 1 -1 1 -1 -1 1 4 -1 -1 -1 -1 -1 1 -1 1 1 -1 1 -1 4 -1 -1 1 1 -1 1 1 1 1 -1 1 1 4 -1 1 -1 -1 1 1 1 1 1 1 1 -1 4 1 -1 -1 1 1 -1 1 1 1 1 -1 1 4 -1 -1 -1 -1 1 -1 1 1 -1 1 -1 -1 |
Hexagonal Prism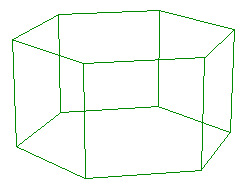
|
a = sqrt(3)/2 b = 1/2
4 a b -b a b b a -b b a -b -b 4 0 1 b 0 1 -b a b -b a b b 4 -a b -b -a b b 0 1 b 0 1 -b 4 -a -b b -a -b -b -a b -b -a b b 4 0 -1 b 0 -1 -b -a -b -b -a -b b 4 0 -1 -b a -b -b a -b b 0 -1 b 6 -a b b 0 1 b a b b a -b b 0 -1 b -a -b b 6 -a b -b 0 1 -b a b -b a -b -b 0 -1 -b -a -b -b |
Truncated Octahedron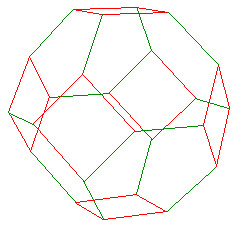
|
a = 0.5
4 1 0 -a 1 -a 0 1 0 a 1 a 0 4 -1 -a 0 -1 0 a -1 a 0 -1 0 -a 4 0 a -1 -a 0 -1 0 -a -1 a 0 -1 4 -a 0 1 0 -a 1 a 0 1 0 a 1 4 a 1 0 0 1 a -a 1 0 0 1 -a 4 0 -1 a -a -1 0 0 -1 -a a -1 0 6 -a 0 1 0 -a 1 0 -1 a -a -1 0 -1 -a 0 -1 0 a 6 -a 0 1 -1 0 a -1 a 0 -a 1 0 0 1 a 0 a 1 6 0 a 1 0 1 a a 1 0 1 a 0 1 0 a a 0 1 6 a 0 1 1 0 a 1 -a 0 a -1 0 0 -1 a 0 -a 1 6 -a 0 -1 0 -a -1 0 -1 -a -a -1 0 -1 -a 0 -1 0 -a 6 -a 0 -1 -1 0 -a -1 a 0 -a 1 0 0 1 -a 0 a -1 6 0 a -1 0 1 -a a 1 0 1 a 0 1 0 -a a 0 -1 6 a 0 -1 1 0 -a 1 -a 0 a -1 0 0 -1 -a 0 -a -1 |
Rhombic Dodecahedron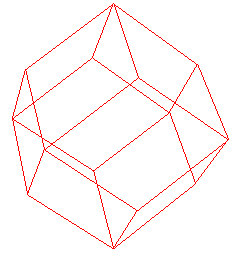
|
a = 1/2
4 1 0 0 a a -a 0 0 -1 a -a -a 4 1 0 0 a -a a 0 0 1 a a a 4 0 0 1 -a -a a -1 0 0 -a a a 4 0 0 -1 -a a -a -1 0 0 -a -a -a 4 0 1 0 a a -a 1 0 0 a a a 4 0 1 0 a a a 0 0 1 -a a a 4 0 1 0 -a a a -1 0 0 -a a -a 4 0 1 0 -a a -a 0 0 -1 a a -a 4 0 -1 0 -a -a -a -1 0 0 -a -a a 4 0 -1 0 a -a -a 0 0 -1 -a -a -a 4 0 -1 0 a -a a 1 0 0 a -a -a 4 0 -1 0 -a -a a 0 0 1 a -a a |
Elongated Rhombic Dodecahedron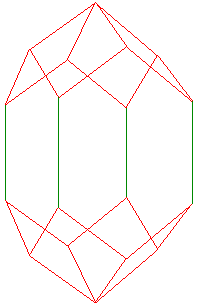
|
a = 1/2 b = 3/2
4 1 0 -a a a -1 0 0 -b a -a -1 4 1 0 a a -a 1 0 0 b a a 1 4 0 0 b -a -a 1 -1 0 a -a a 1 4 0 0 -b -a a -1 -1 0 -a -a -a -1 4 0 -1 a -a -a 1 0 0 b a -a 1 4 0 1 a a a 1 0 0 b -a a 1 4 0 -1 -a a -a -1 0 0 -b -a -a -1 4 0 1 -a -a a -1 0 0 -b a a -1 6 -a -a 1 0 -1 a 0 -1 -a -a -a -1 -1 0 -a -1 0 a 6 -a a 1 0 1 a 0 1 -a -a a -1 -1 0 -a -1 0 a 6 a a 1 1 0 a 1 0 -a a a -1 0 1 -a 0 1 a 6 a -a 1 1 0 a 1 0 -a a -a -1 0 -1 -a 0 -1 a |