Reuleaux TriangleWritten by Paul BourkeApril 2009
The Reuleaux triangle is formed by connecting up the vertices of an equilateral triangle with arcs, the arc between any two vertices has its center at the third vertex. 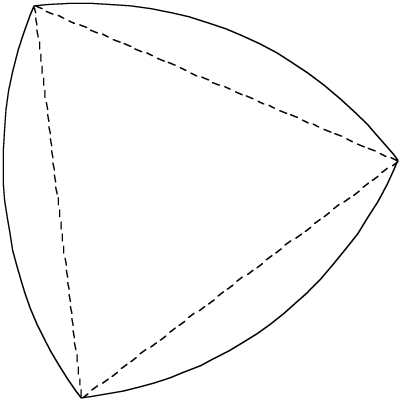
The Reuleaux triangle has the unique property that it is the smallest area of any curve of constant width. Constant width means that the distance between any two parallel tangential lines is constant. This is obviously a property of a circle but it is also true for a family of other curves such as the Reuleaux triangle. By adding together the area of the three arc sections and subtracting the overlapping central portion (the equilateral triangle) the area can be shown to be as follows where r is the radius of the arcs (also the diameter of the triangle). Since the diameter is constant this is an example of why simply measuring diameter is not an algorithm for determining if an object/shape is a circle. |